This is the multi-page printable view of this section. Click here to print.

Return to the regular view of this page.

DBSCAN

Density Based Spatial Clustering of Application with Noise
Video DBSCAN : Density- Based Spatial Clustering of Applications with Noise | Explained with Example

1 - DBSCAN

Density Based Spatial Clustering of Application with Noise
Issues with K-Means
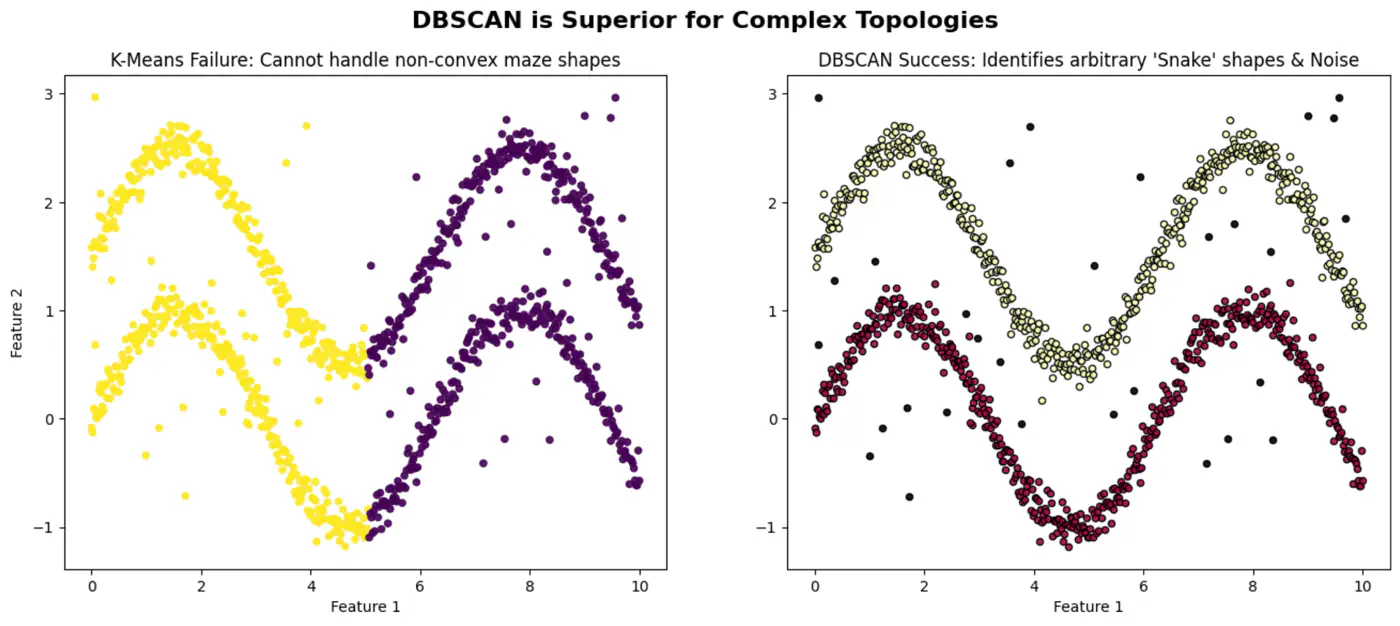
  • Non-Convex Shapes: K-Means can not find ‘crescent’ or ‘ring’ shape clusters.
  • Noise: K-Means forces every point into a cluster, even outliers.
Main Question for Clustering ?

K-Means asks:

  • “Which center is closest to this point?”

DBSCAN asks:

  • “Is this point part of a dense neighborhood?”
Intuition
Cluster is a contiguous region of high density in the data space, separated from other clusters by areas of low density.
DBSCAN

Groups closely packed data points into clusters based on their density, and marks points that lie alone in low-density regions as outliers or noise.

Note: Unlike K-means, DBSCAN can find arbitrarily shaped clusters and does not require the number of clusters to be specified beforehand.

Hyper-Parameters
  1. Epsilon (eps or \(\epsilon\)):
  • Radius that defines the neighborhood around a data point.
  • If it’s too small, many points will be noise, and if too large, distinct clusters may merge.
  1. Minimum Points(minPts or min_samples):
  • Minimum number of data points required within a point’s -neighborhood for that point to be considered a dense region (a core point).
  • Defines threshold for ‘density’.
  • Rule of thumb: minPts dimensions + 1; use larger value for noisy data (minPts 2*dimensions).
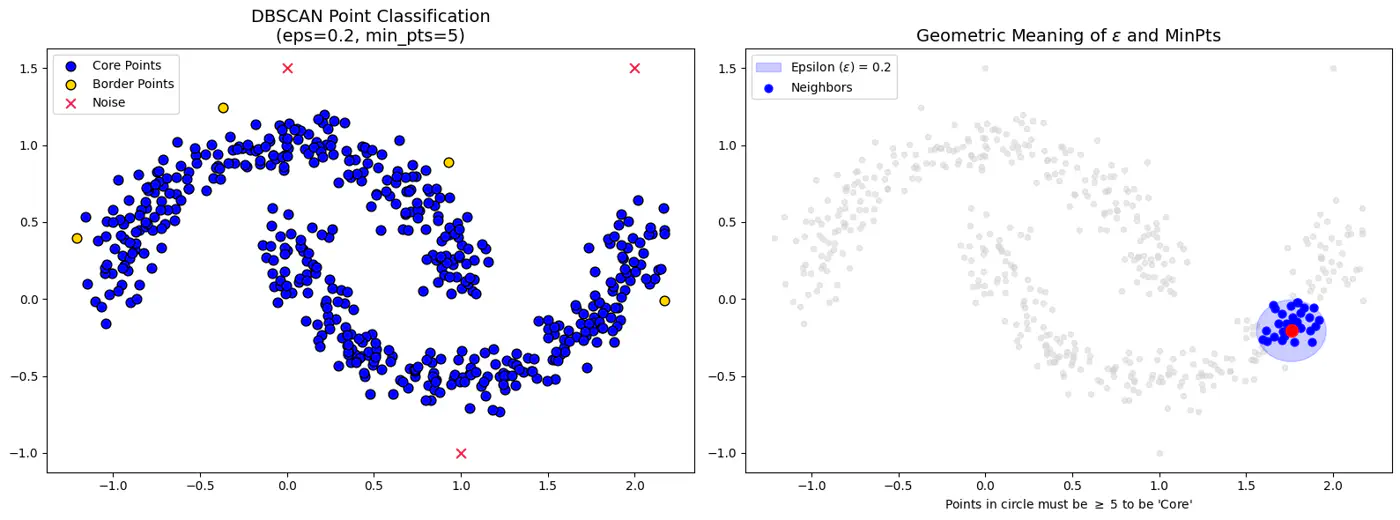
Types of Points
  • Core Point:
    • If it has at least minPts (including itself) within its -neighborhood.
    • Forms the dense backbone of the clusters and can expand them.
  • Border Point:
    • If it has at fewer than minPts within its -neighborhood but falls within the -neighborhood of a core point.
    • Border points belong to a cluster but cannot expand it further.
  • Noise Point (Outlier):
    • If it is neither a core point nor a border point, i.e., it is not density-reachable from any core point.
    • Not assigned to any cluster.
DBSCAN Algorithm
  1. Random Start:
  • Mark all points as unvisited; pick an arbitrary unvisited point ‘P’ from the dataset.
  1. Density Check:
  • Check the point P’s ϵ-neighborhood.
  • If ‘P’ has at least minPts, it is identified as a core point, and a new cluster is started.
  • If it has fewer than minPts, the point is temporarily labeled as noise (it might become a border point later).
  1. Cluster Expansion:
  • Recursively visit all points in P’s ϵ-neighborhood.
  • If they are also core points, their neighbors are added to the cluster.
  1. Iteration :
  • This ‘density-reachable’ logic continues until the cluster is fully expanded.
  • The algorithm then picks another unvisited point and repeats the process, discovering new clusters or marking more points as noise until all points are processed.

DBSCAN can correctly detect non-spherical clusters.

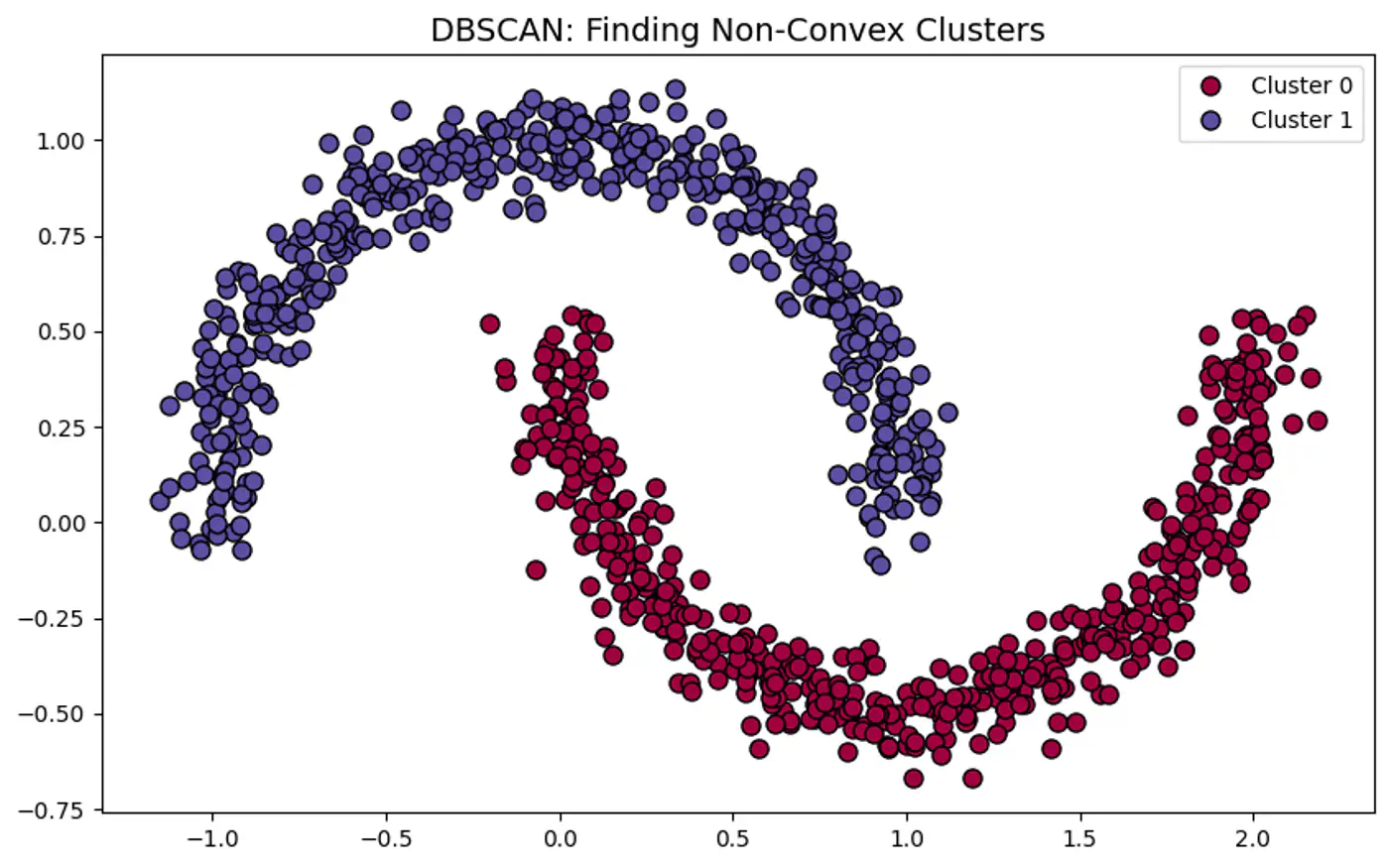
images/machine_learning/unsupervised/dbscan/dbscan/slide_11_01.png

DBSCAN Points and Epsilon-Neighborhood.

images/machine_learning/unsupervised/dbscan/dbscan/slide_12_01.png
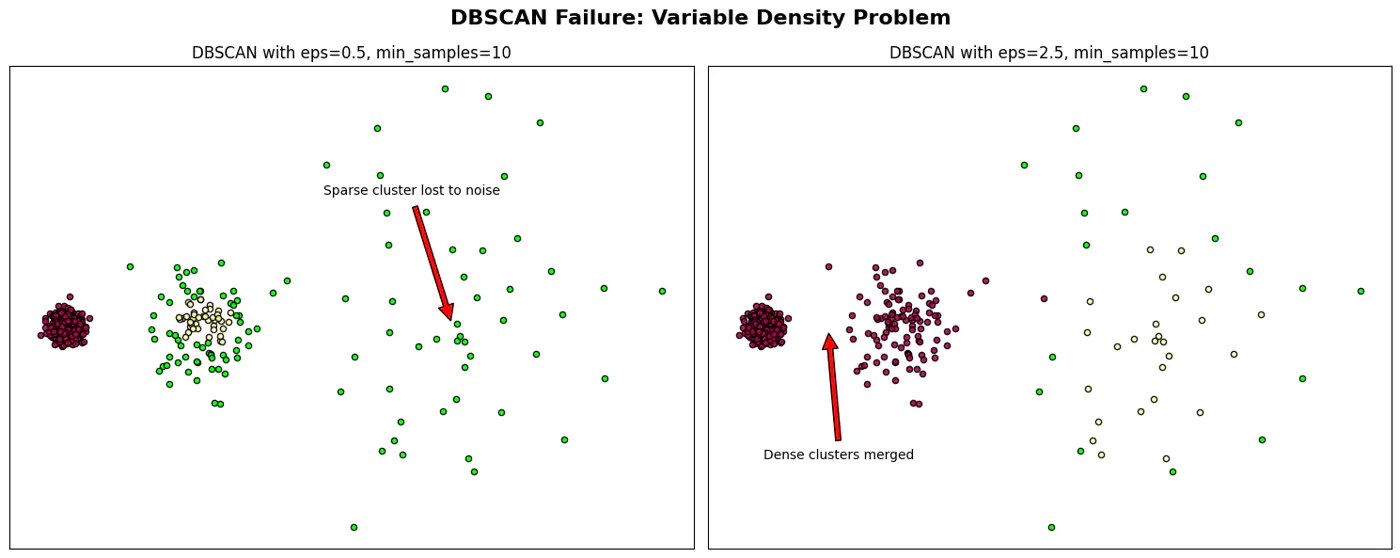
When DBSCAN Fails ?
  • Varying Density Clusters:
    • Say A cluster is very dense and B is sparse, a single cannot satisfy both clusters.
  • High Dimensional Data:
    • ‘Curse of Dimensionality’ - In high-dimensional space, the distance between any two points converge.

Note: Sensitive to parameter eps and minPts; tricky to get it work.

DBSCAN Failure and Epsilon ((\epsilon)

images/machine_learning/unsupervised/dbscan/dbscan/slide_14_01.png
When to use DBSCAN ?

  • Arbitrary Cluster Shapes:

    • When clusters are intertwined, nested, or ‘moon-shaped’; where K-Means would fail by splitting them.

  • Presence of Noise and Outliers:

    • Robust to noise and outliers because it explicitly identifies low-density points as noise (labeled as -1) rather than forcing them into a cluster.
    images/machine_learning/unsupervised/dbscan/dbscan/snake_shape.png
Video DBSCAN : Density- Based Spatial Clustering of Applications with Noise | Explained with Example

End of Section