End of Section
This is the multi-page printable view of this section. Click here to print.
Gaussian Mixture Model
1 - Gaussian Mixture Models
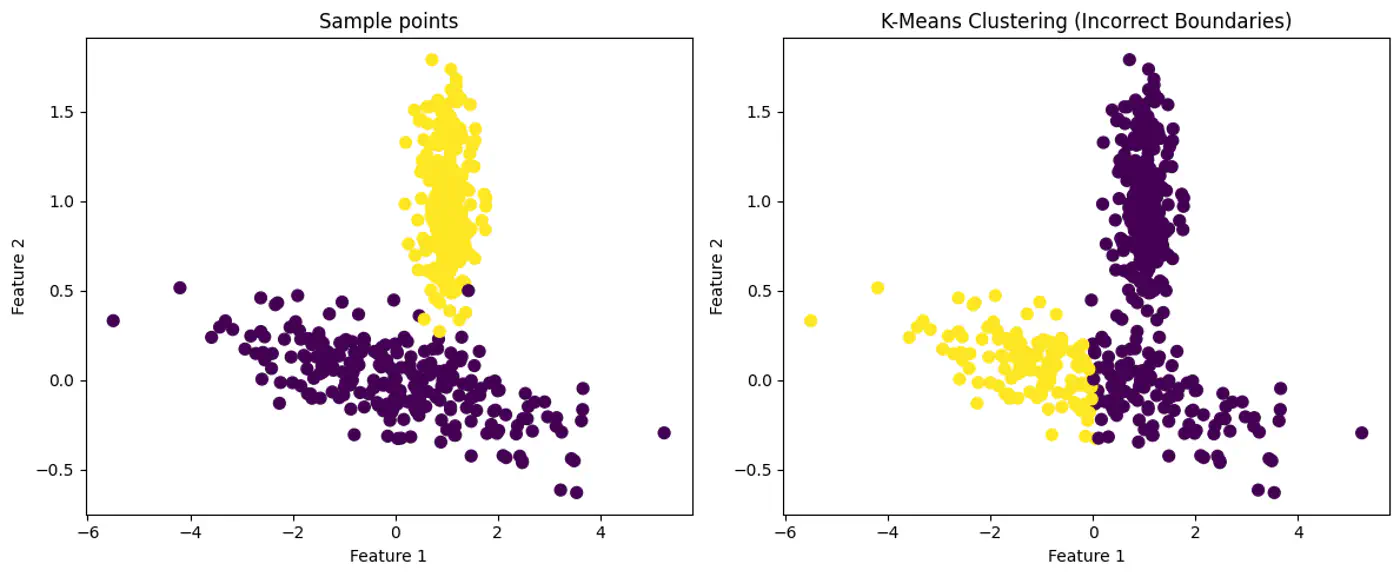
- K-means uses Euclidean distance and assumes that clusters are spherical (isotropic) and have the same variance across all dimensions.
- Places a circle or sphere around each centroid.
- What if the clusters are elliptical ? 🤔
👉K-Means Fails with Elliptical Clusters.
💡GMM: ‘Probabilistic evolution’ of K-Means
⭐️ GMM provides soft assignments and can model elliptical clusters by accounting for variance and correlation between features.
Note: GMM assumes that all data points are generated from a mixture of a finite number of Gaussian Distributions with unknown parameters.
👉GMM can Model Elliptical Clusters.
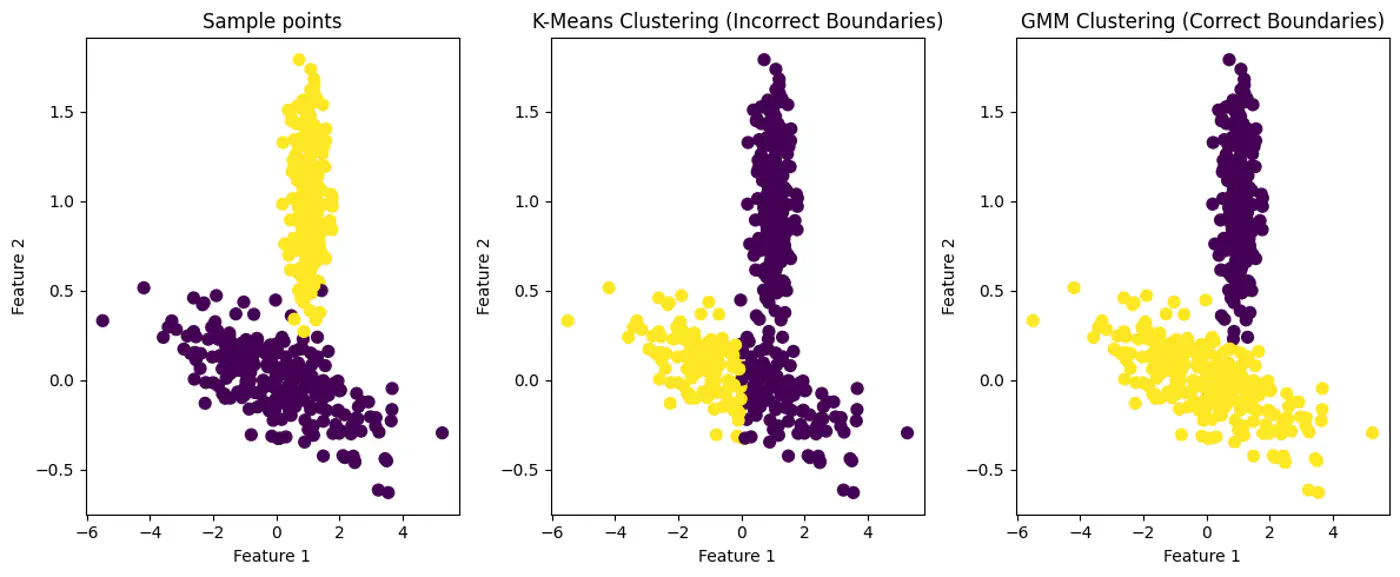
💡‘Combination of probability distributions’.
👉Soft Assignment: Instead of a simple ‘yes’ or ’no’ for cluster membership, a data point is assigned a set of probabilities, one for each cluster.
e.g: A data point might have a 60% probability of belonging to cluster ‘A’, 30% probability for cluster ‘B’, and 10% probability for cluster ‘C’.
👉Gaussian Mixture Model Example:
Note: The term \(1/(\sqrt{2\pi \sigma ^{2}})\) is a normalization constant to ensure the total area under the curve = 1.
👉Multivariate Gaussian Example:
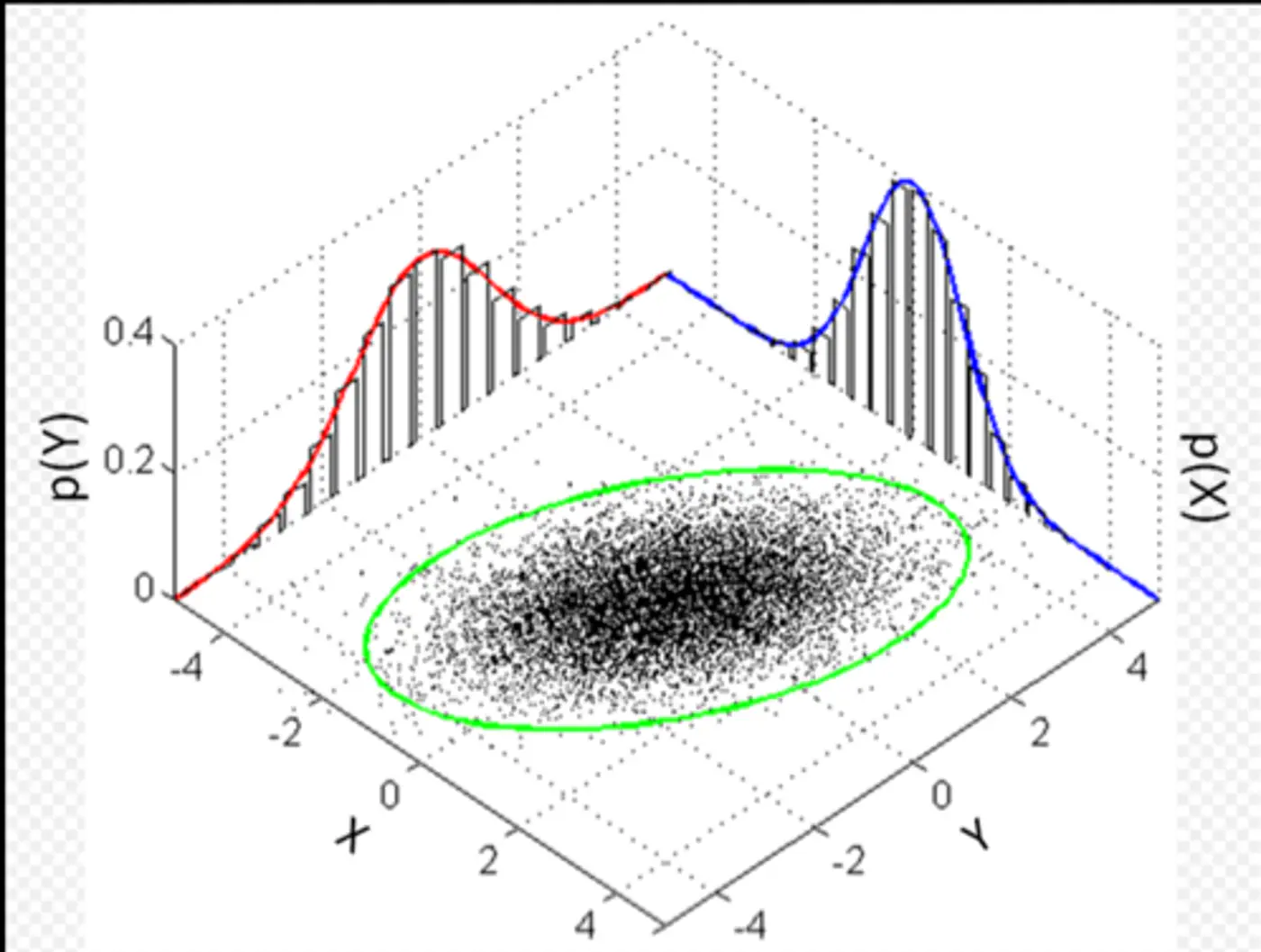
Whenever we have multivariate Gaussian, then the variables may be independent or correlated.
👉Feature Covariance:
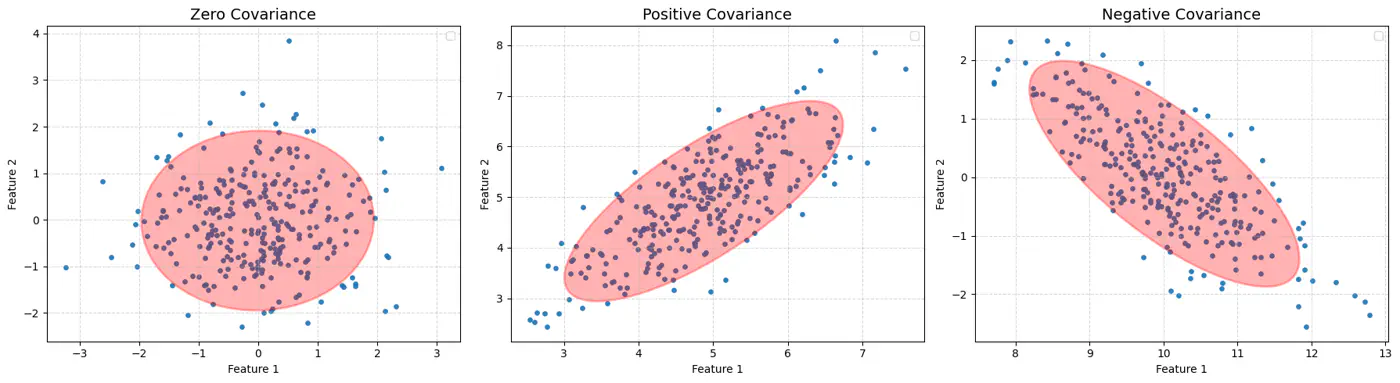
👉Gaussian Mixture with PDF
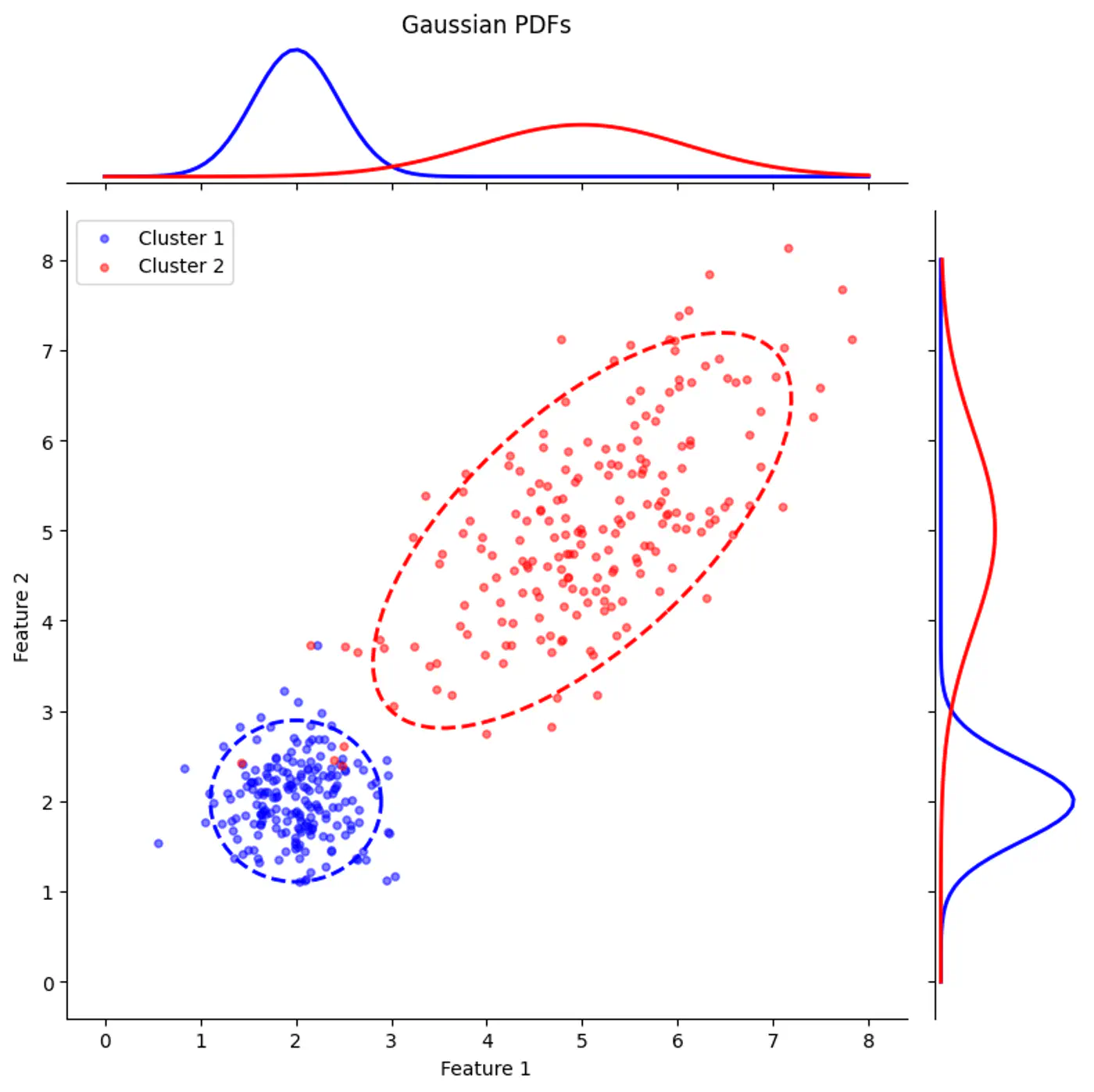
👉Gaussian Mixture (2D)
End of Section
2 - Latent Variable Model
⭐️Probabilistic model that assumes data is generated from a mixture of several Gaussian (normal) distributions with unknown parameters.
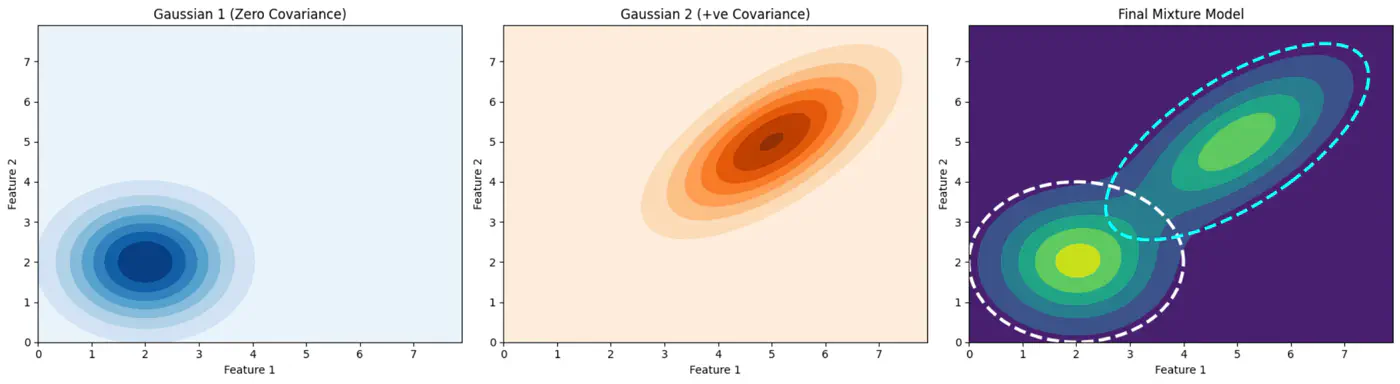
🎯GMM represents the probability density function of the data as a weighted sum of ‘K’ component Gaussian densities.
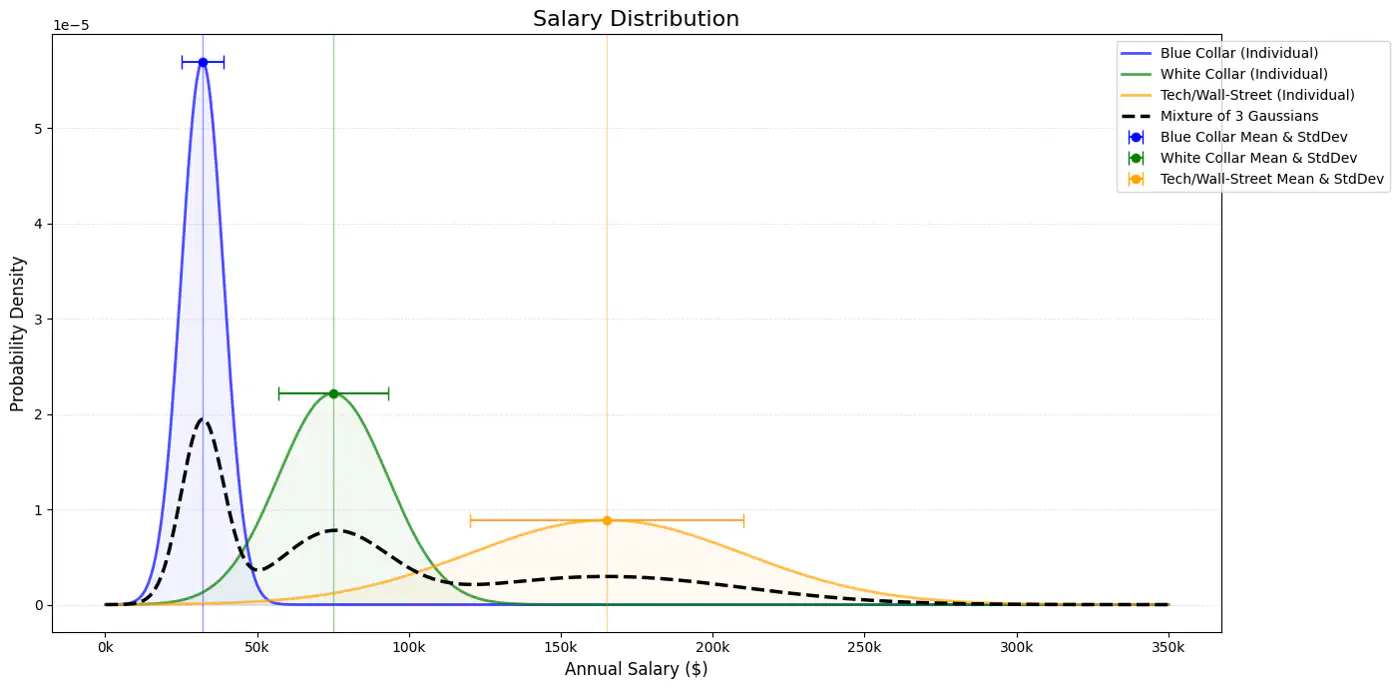
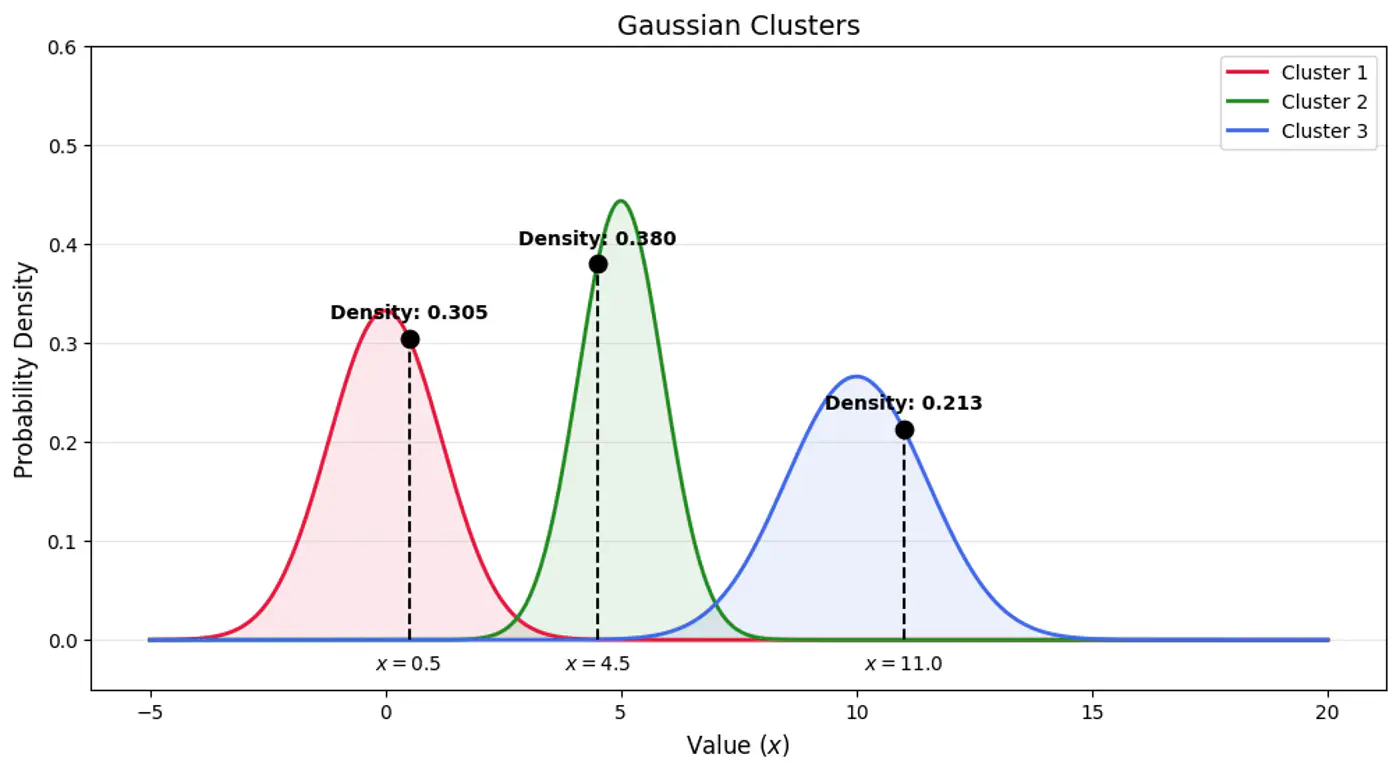
👉Below plot shows the probability of a point being generated by 3 different Gaussians.
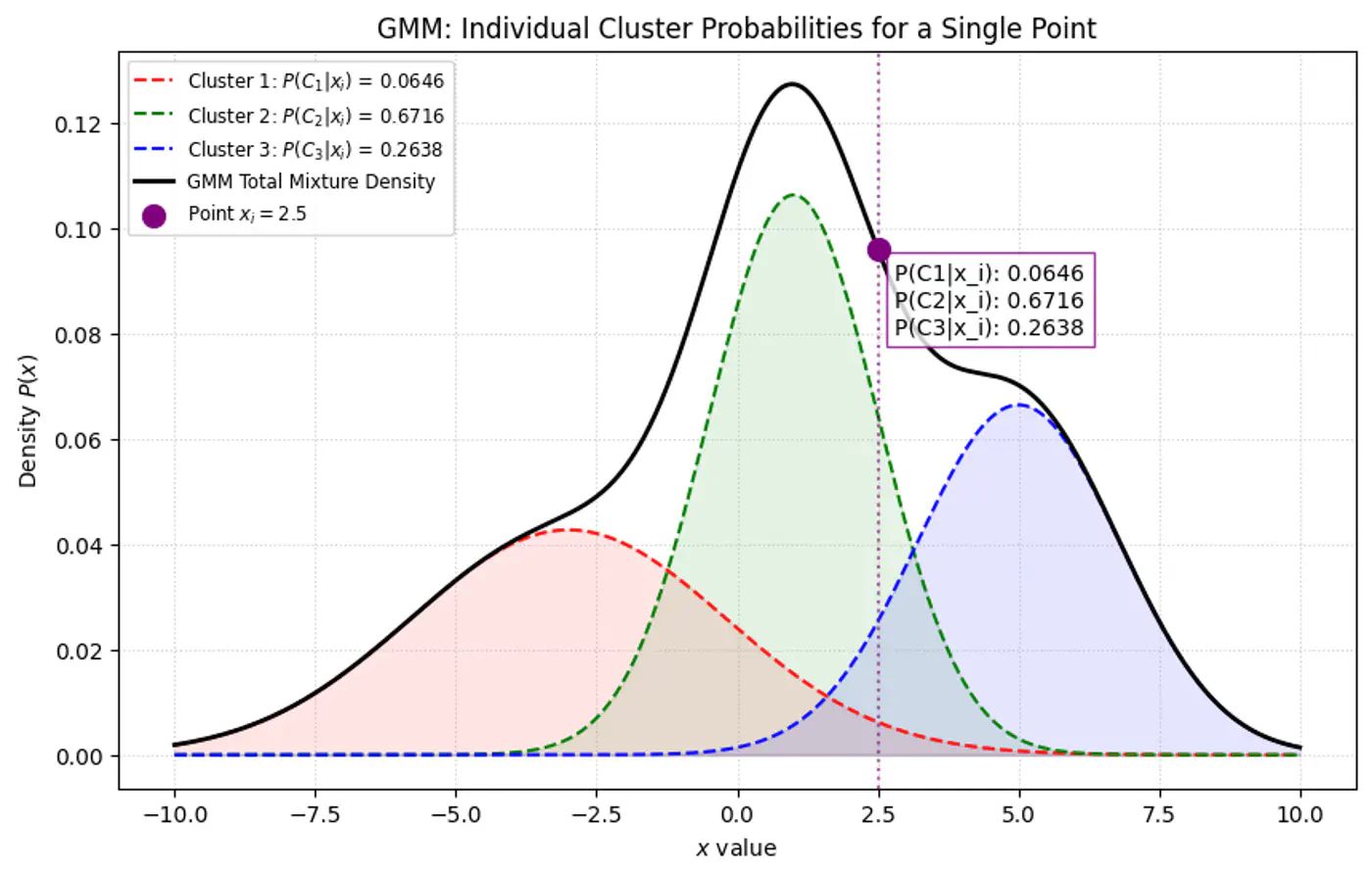
Overall density \(p(x_i|\mathbf{\theta })\) for a data point ‘\(x_i\)’:
\[p(x_i|\mathbf{\mu},\mathbf{\Sigma} )=\sum _{k=1}^{K}\pi _{k}\mathcal{N}(x_i|\mathbf{\mu }_{k},\mathbf{\Sigma }_{k})\]- K: number of component Gaussians.
- \(\pi_k\): mixing coefficient (weight) of the k-th component, such that, \(\pi_k \ge 0\) and \(\sum _{k=1}^{K}\pi _{k}=1\).
- \(\mathcal{N}(x_i|\mathbf{\mu }_{k},\mathbf{\Sigma }_{k})\): probability density function of the k-th Gaussian component with mean \(\mu_k\) and covariance matrix \(\Sigma_k\).
- \(\mathbf{\theta }=\{(\pi _{k},\mathbf{\mu }_{k},\mathbf{\Sigma }_{k})\}_{k=1}^{K}\): complete set of parameters to be estimated.
Note: \(\pi _{k}\approx \frac{\text{Number\ of\ points\ in\ cluster\ }k}{\text{Total\ number\ of\ points\ }(N)}\)
👉 Weight of the cluster is proportional to the number of points in the cluster.
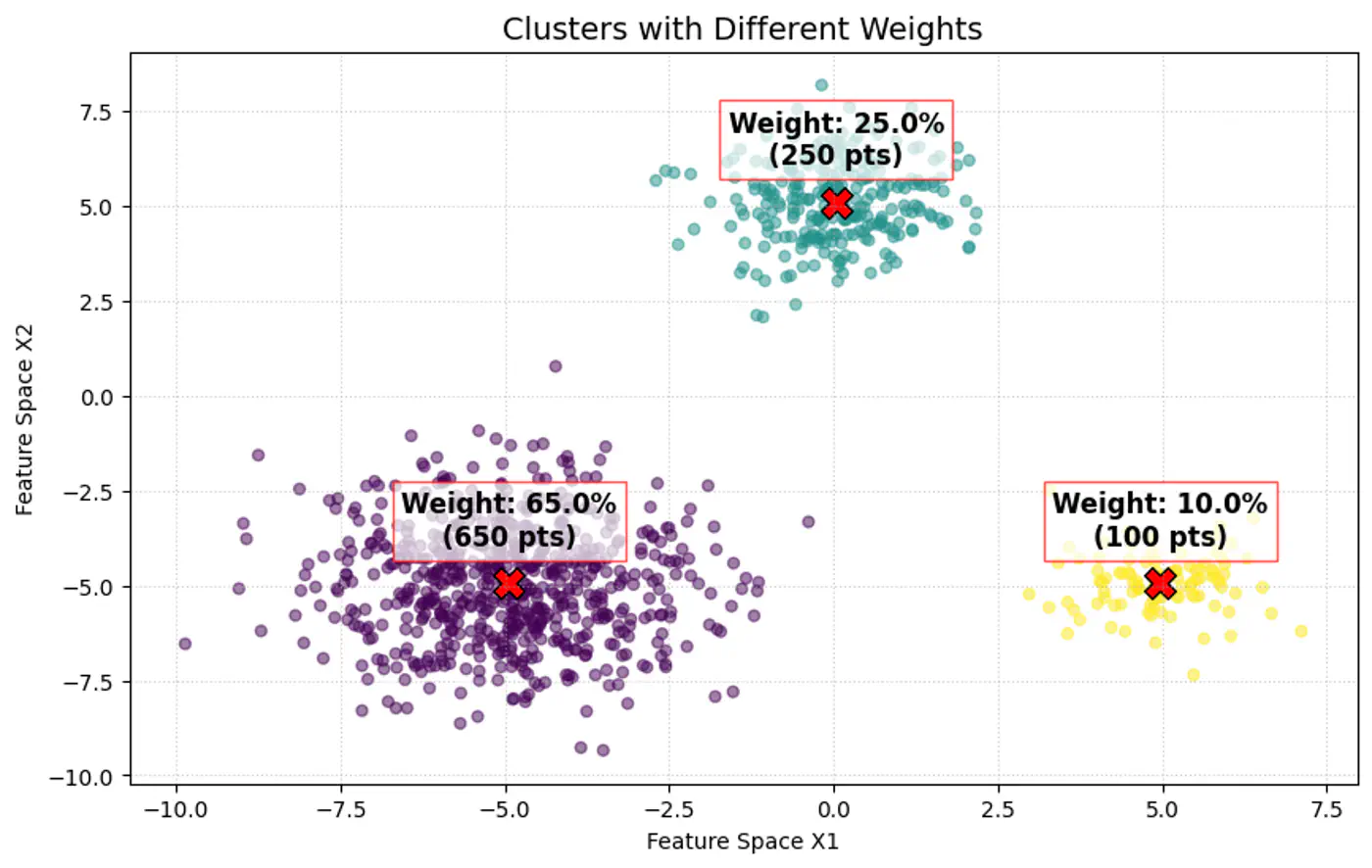
👉Below image shows the weighted Gaussian PDF, given the weights of clusters.
🎯 Goal of a GMM optimization is to find the set of parameters \(\Theta =\{(\pi _{k},\mu _{k},\Sigma _{k})\mid k=1,\dots ,K\}\) that maximize the likelihood of observing the given data.
\[L(\Theta |X)=\sum _{i=1}^{N}\log P(x_i|\Theta )=\sum _{i=1}^{N}\log \left(\sum _{k=1}^{K}\pi _{k}\mathcal{N}(x_i|\mu _{k},\Sigma _{k})\right)\]- 🦀 \(\log (A+B)\) cannot be simplified.
- 🦉So, is there any other way ?
⭐️Imagine we are measuring the heights of people in a college.
- We see a distribution with two peaks (bimodal).
- We suspect there are two underlying groups:
- Group A (Men) and Group B (Women).
Observation:
- Observed Variable (X): Actual height measurements.
- Latent Variable (Z): The ‘label’ (Man or Woman) for each person.
Note: We did not record gender, so it is ‘hidden’ or ‘latent’.
⭐️GMM is a latent variable model, meaning each data point \(\mathbf{x}_{i}\) is assumed to have an associated unobserved (latent) variable \(z_{i}\in \{1,\dots ,K\}\) indicating which component generated it.
Note: We observe the data point, but we do not observe which cluster it belongs to (\(z_i\)).
👉If we knew the value of \(z_i\) (component indicator) for every point, estimating the parameters of each Gaussian component would be straightforward.
Note: The challenge lies in estimating both the parameters of the Gaussians and the values of the latent variables simultaneously.
- With ‘z’ unknown:
- maximize: \[ \log \sum _{k}\pi _{k}\mathcal{N}(x_{i}|\mu _{k},\Sigma _{k}) = \log \Big(\pi _{1}\mathcal{N}(x_{i}\mid \mu _{1},\Sigma _{1})+\pi _{2}\mathcal{N}(x_{i}\mid \mu _{2},\Sigma _{2})+ \dots + \pi _{k}\mathcal{N}(x_{i}\mid \mu _{k},\Sigma _{k})\Big)\]
- \(\log (A+B)\) cannot be simplified.
- maximize: \[ \log \sum _{k}\pi _{k}\mathcal{N}(x_{i}|\mu _{k},\Sigma _{k}) = \log \Big(\pi _{1}\mathcal{N}(x_{i}\mid \mu _{1},\Sigma _{1})+\pi _{2}\mathcal{N}(x_{i}\mid \mu _{2},\Sigma _{2})+ \dots + \pi _{k}\mathcal{N}(x_{i}\mid \mu _{k},\Sigma _{k})\Big)\]
- With ‘z’ known:
- The log-likelihood of the ‘complete data’ simplifies into a sum of logarithms:
\[\sum _{i}\log (\pi _{z_{i}}\mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}}))\]
- Every point is assigned to exactly one cluster, so the sum disappears because there is only one cluster responsible for that point.
- The log-likelihood of the ‘complete data’ simplifies into a sum of logarithms:
\[\sum _{i}\log (\pi _{z_{i}}\mathcal{N}(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}}))\]
Note: This allows the logarithm to act directly on the exponential term of the Gaussian, leading to simple linear equations.
👉When ‘z’ is known, every data point is ‘labeled’ with its parent component.
To estimate the parameters (mean \(\mu_k\) and covariance \(\Sigma_k\)) for a specific component ‘k’ :
- Gather all data points \(x_i\), where \(z_i\)= k.
- Calculate the standard Maximum Likelihood Estimate.(MLE) for that single Gaussian using only those points.
⭐️ Knowing ‘z’ provides exact counts and component assignments, leading to direct formulae for the parameters:
- Mean (\(\mu_k\)): Arithmetic average of all points assigned to component ‘k’.
- Covariance (\(\Sigma_k\)): Sample covariance of all points assigned to component ‘k’.
- Mixing Weight (\(\pi_k\)): Fraction of total points assigned to component ‘k’.
End of Section
3 - Expectation Maximization
- If we knew the parameters (\(\mu, \Sigma, \pi\)) we could easily calculate which cluster ‘z’ each point belongs to (using probability).
- If we knew the cluster assignments ‘z’ of each point, we could easily calculate the parameters for each cluster (using simple averages).
🦉But we do not know either of them, as the parameters of the Gaussians - we aim to find and cluster indicator latent variable is hidden.
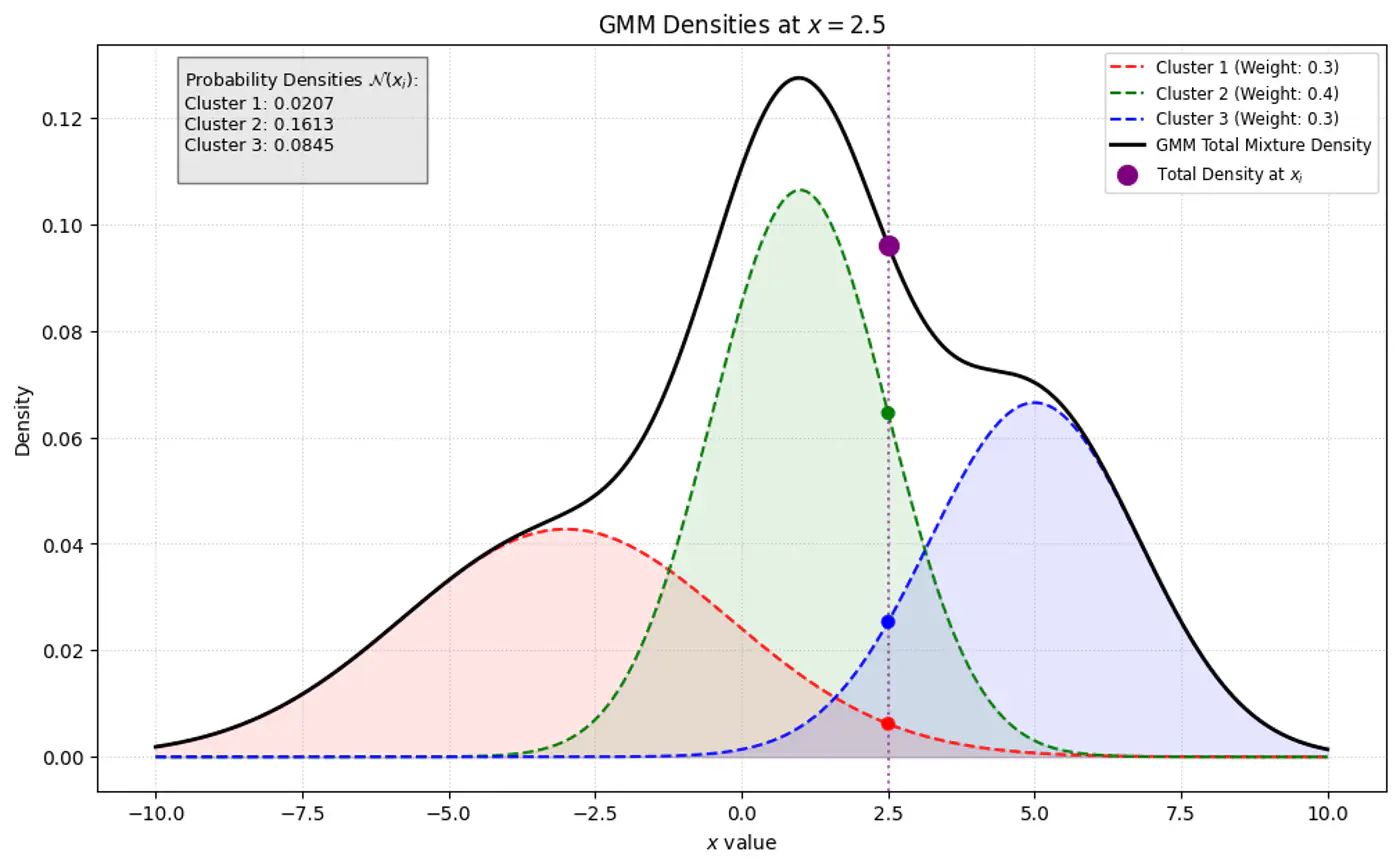
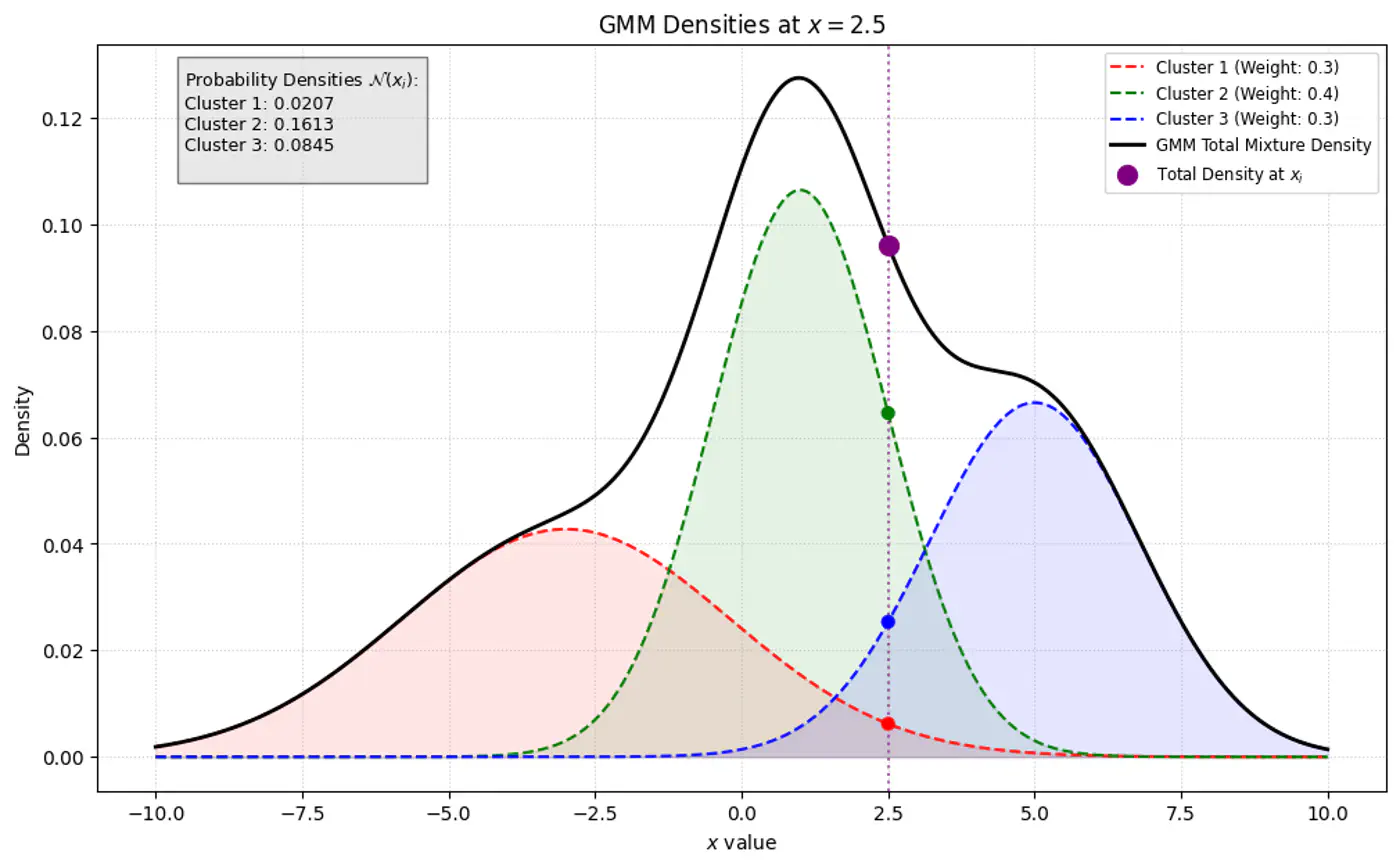
⛳️ Find latent cluster indicator variable \(z_{ik}\).
But \(z_{ik}\) is a ‘hard’ assignment’ (either ‘0’ or ‘1’).
- 🦆 Because we do not observe ‘z’, we use another variable ‘Responsibility’ (\(\gamma_{ik}\)) as a ‘soft’ assignment (value between 0 and 1).
- 🐣 \(\gamma_{ik}\) is the expected value of the latent variable \(z_{ik}\), given the observed data \(x_{i}\) and parameters \(\Theta\). \[\gamma _{ik}=E[z_{ik}\mid x_{i},\theta ]=P(z_{ik}=1\mid x_{i},\theta )\]
Note: \(\gamma_{ik}\) is the posterior probability (or ‘responsibility’) that cluster ‘k’ takes for explaining data point \(x_{i}\).
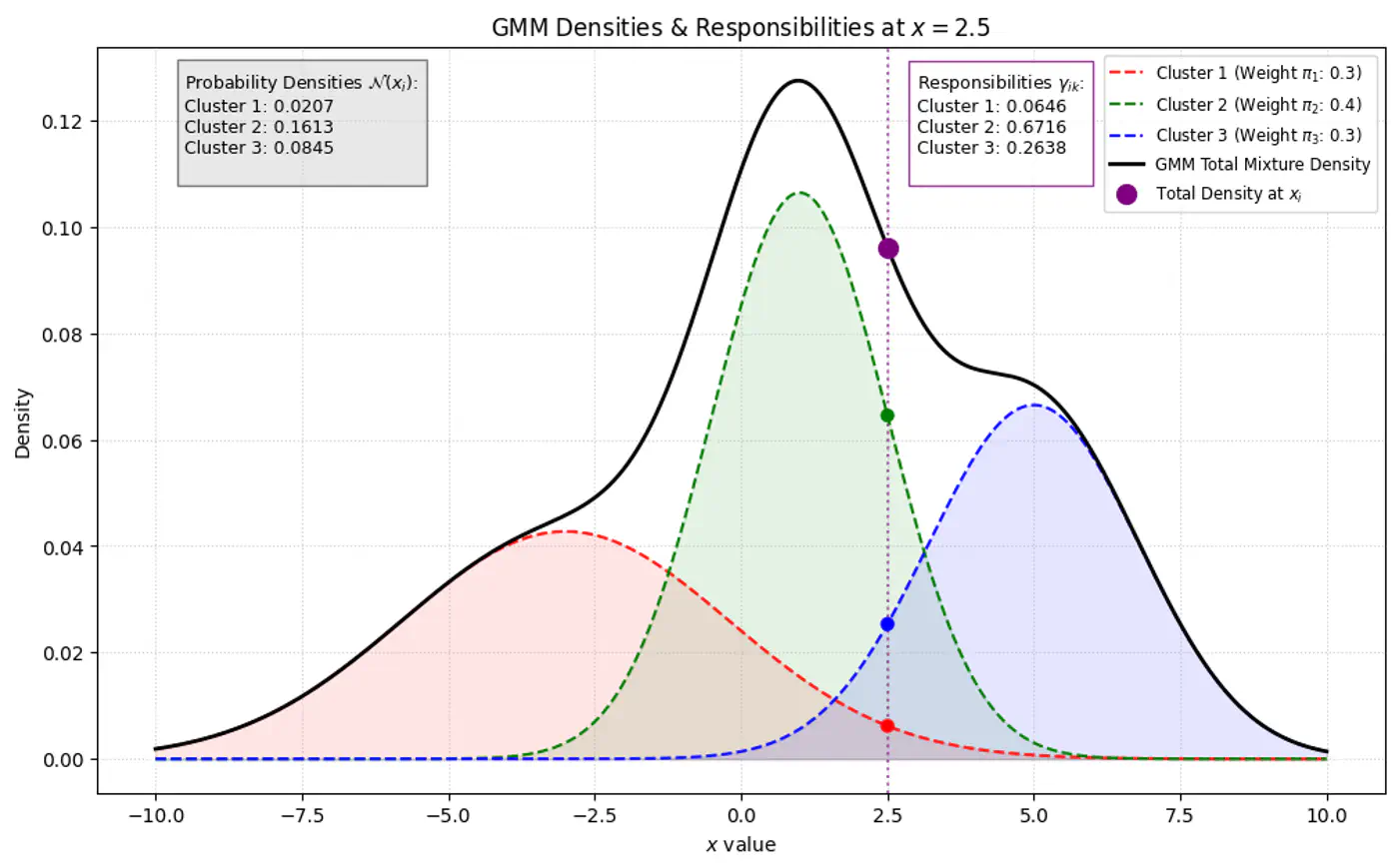
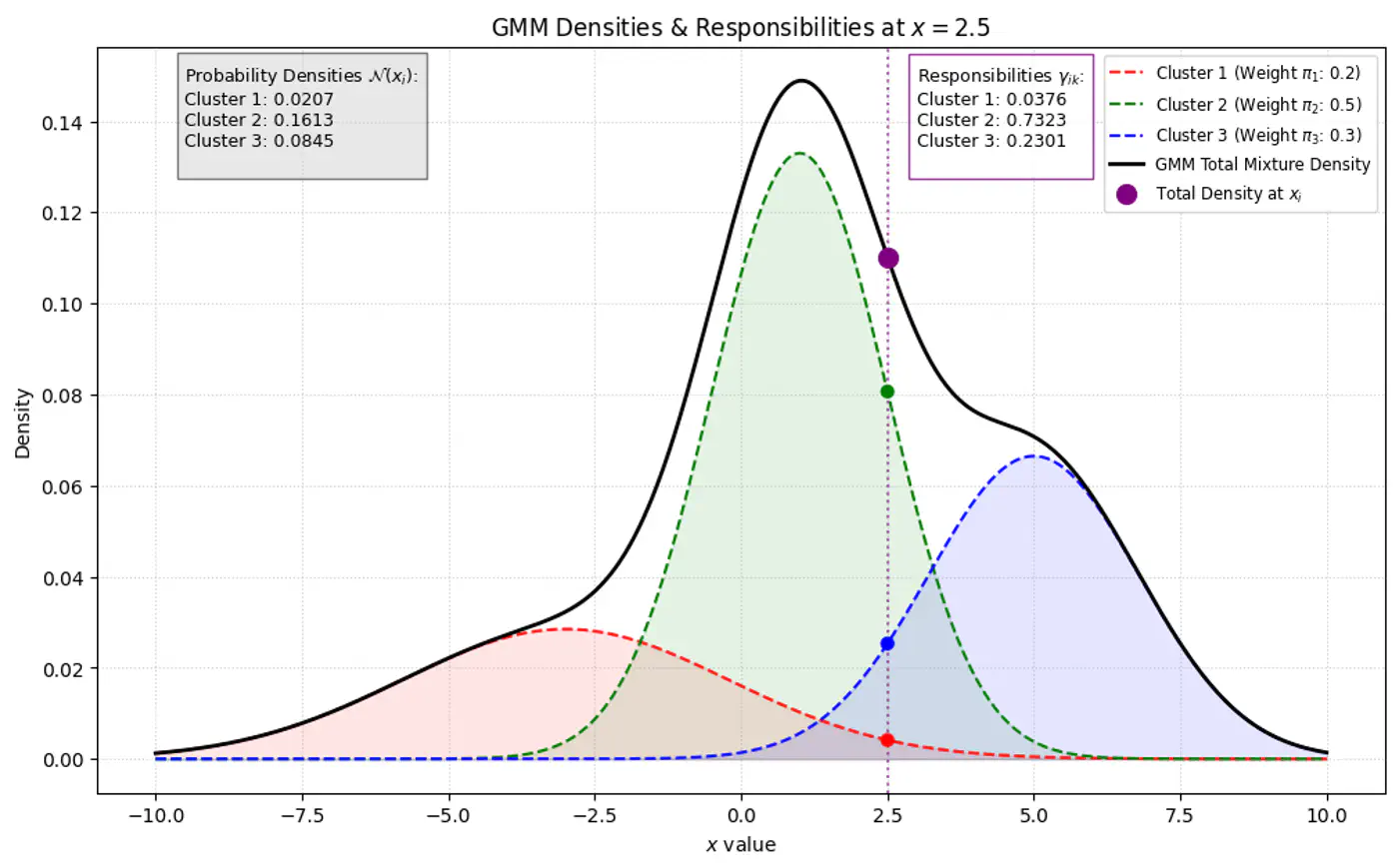
⭐️Using Bayes’ Theorem, we derive responsibility (posterior probability that component ‘k’ generated data point \(x_i\)) by combining the prior/weights (\(\pi_k\)) and the likelihood (\(\mathcal{N}(x_{i}\mid \mu _{k},\Sigma _{k})\)).
\[\gamma _{ik}= P(z_{ik}=1\mid x_{i},\theta ) = \frac{P(z_{ik}=1)P(x_{i}\mid z_{ik}=1)}{P(x_{i})}\]\[\gamma _{ik}=\frac{\pi _{k}\mathcal{N}(x_{i}\mid \mu _{k},\Sigma _{k})}{\sum _{j=1}^{K}\pi _{j}\mathcal{N}(x_{i}\mid \mu _{j},\Sigma _{j})}\]👉Bayes’ Theorem: \(P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}\)
👉 GMM Densities at point
👉GMM Densities at point (different cluster weights)
- Initialization: Assign initial values to parameters (\(\mu, \Sigma, \pi\)), often using K-Means results.
- Expectation Step (E): Calculate responsibilities; provides ‘soft’ assignments of points to clusters.
- Maximization Step (M): Update parameters using responsibilities as weights to maximize the expected log-likelihood.
- Convergence: Repeat ‘E’ and ‘M’ steps until the change in log-likelihood falls below a threshold.
👉Given our current guess of the clusters, what is the probability that point \(x_i\) came from cluster ‘k’ ?
\[\gamma (z_{ik})=p(z_{i}=k|\mathbf{x}_{i},\mathbf{\theta }^{(\text{old})})=\frac{\pi _{k}^{(\text{old})}\mathcal{N}(\mathbf{x}_{i}|\mathbf{\mu }_{k}^{(\text{old})},\mathbf{\Sigma }_{k}^{(\text{old})})}{\sum _{j=1}^{K}\pi _{j}^{(\text{old})}\mathcal{N}(\mathbf{x}_{i}|\mathbf{\mu }_{j}^{(\text{old})},\mathbf{\Sigma }_{j}^{(\text{old})})}\]\(\pi_k\) : Probability that a randomly selected data point \(x_i\) belongs to the k-th component before we even look at the specific value of \(x_i\), such that \(\pi_k \ge 0\) and \(\sum _{k=1}^{K}\pi _{k}=1\).
👉Update the parameters (\(\mu, \Sigma, \pi\)) by calculating weighted versions of the standard MLE formulas using responsibilities as weight 🏋️♀️.
\[ \begin{align*} &\bullet \mathbf{\mu }_{k}^{(\text{new})}=\frac{1}{N_{k}}\sum _{i=1}^{N}\gamma (z_{ik})\mathbf{x}_{i} \\ &\bullet \mathbf{\Sigma }_{k}^{(\text{new})}=\frac{1}{N_{k}}\sum _{i=1}^{N}\gamma (z_{ik})(\mathbf{x}_{i}-\mathbf{\mu }_{k}^{(\text{new})})(\mathbf{x}_{i}-\mathbf{\mu }_{k}^{(\text{new})})^{\top } \\ &\bullet \pi _{k}^{(\text{new})}=\frac{N_{k}}{N} \end{align*} \]- where, \(N_{k}=\sum _{i=1}^{N}\gamma (z_{ik})\) is the effective number of points assigned to component ‘k'.
End of Section