End of Section
This is the multi-page printable view of this section. Click here to print.
Hierarchical Clustering
Hierarchical Clustering
1 - Hierarchical Clustering
Hierarchical Clustering
Issues with K-Means
- 🤷 We might not know in advance the number of distinct clusters ‘k’ in the dataset.
- 🕸️ Also, sometimes the dataset may contain a nested structure or some inherent hierarchy, such as, file system, organizational chart, biological lineages, etc.
Hierarchical Clustering
⭐️ Method of cluster analysis that seeks to build a hierarchy of clusters, resulting in a tree like structure called dendrogram.
👉Hierarchical clustering allows us to explore different possibilities (of ‘k’) by cutting the dendrogram at various levels.
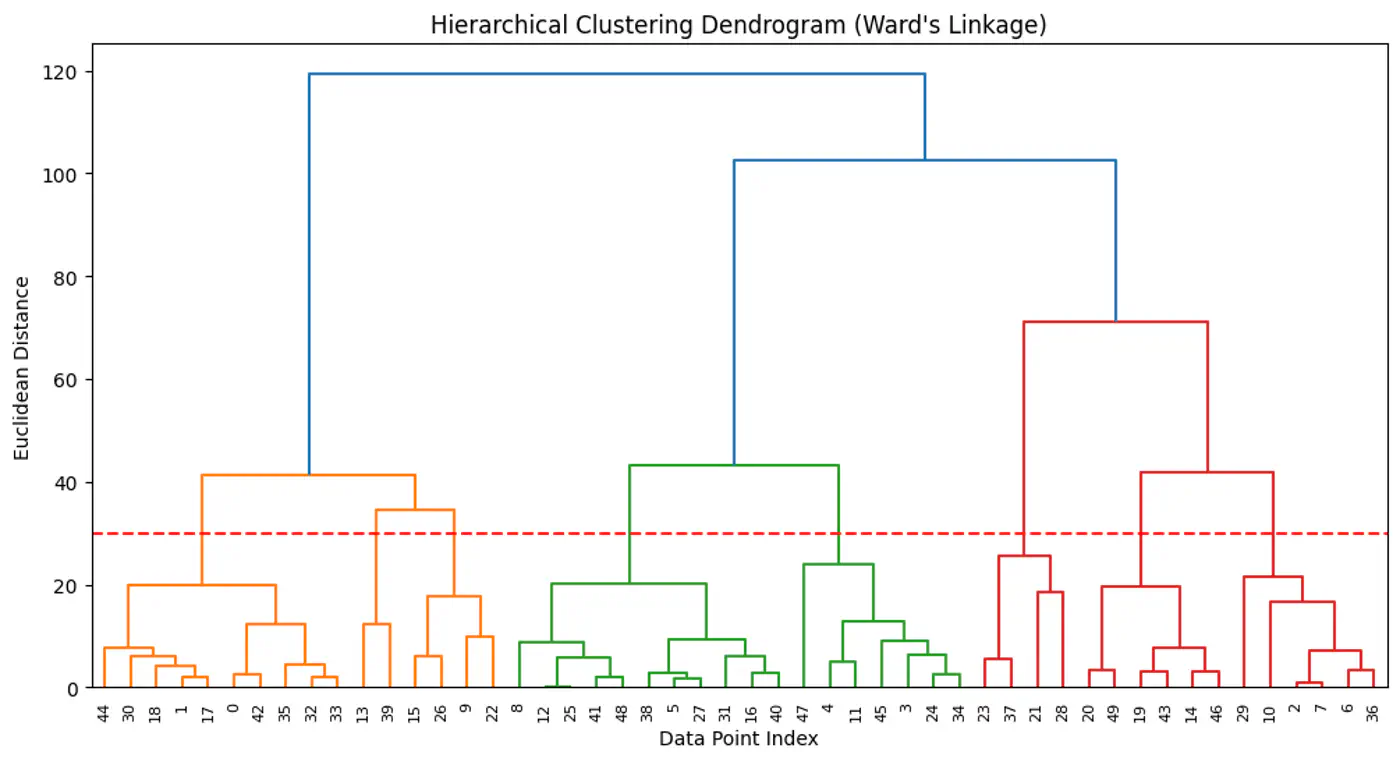
2 Philosophies
Agglomerative (Bottom-Up):
Most common, also known as Agglomerative Nesting (AgNes).
- Every data point starts as its own cluster.
- In each step, merge the two ‘closest’ clusters.
- Repeat step 2, until all points are merged in a single cluster.
Divisive (Top-Down):
- All data points start in one large cluster.
- In each step, divide the cluster into two halves.
- Repeat step 2, until every point is its own cluster.
Agglomerative Clustering Example:
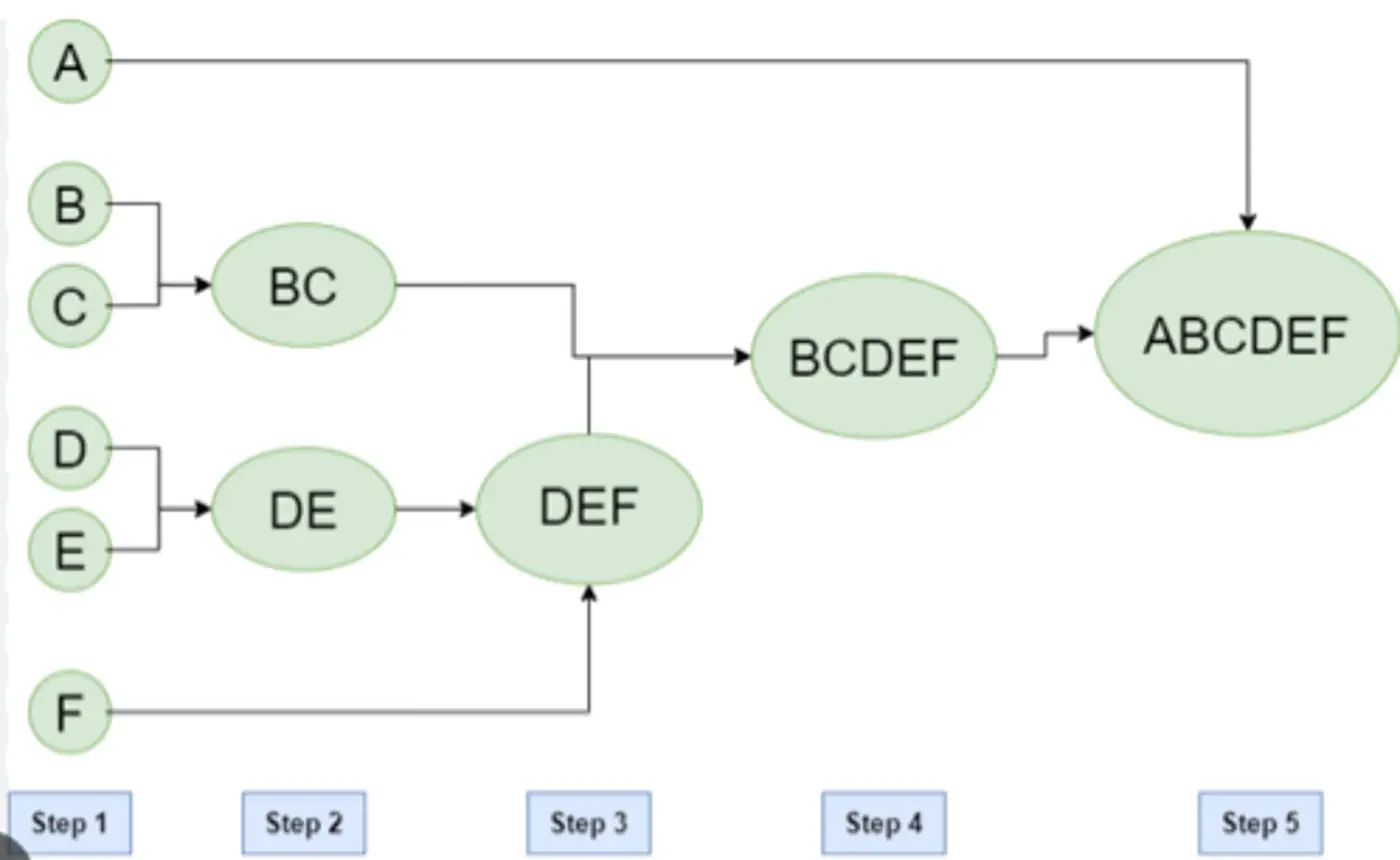
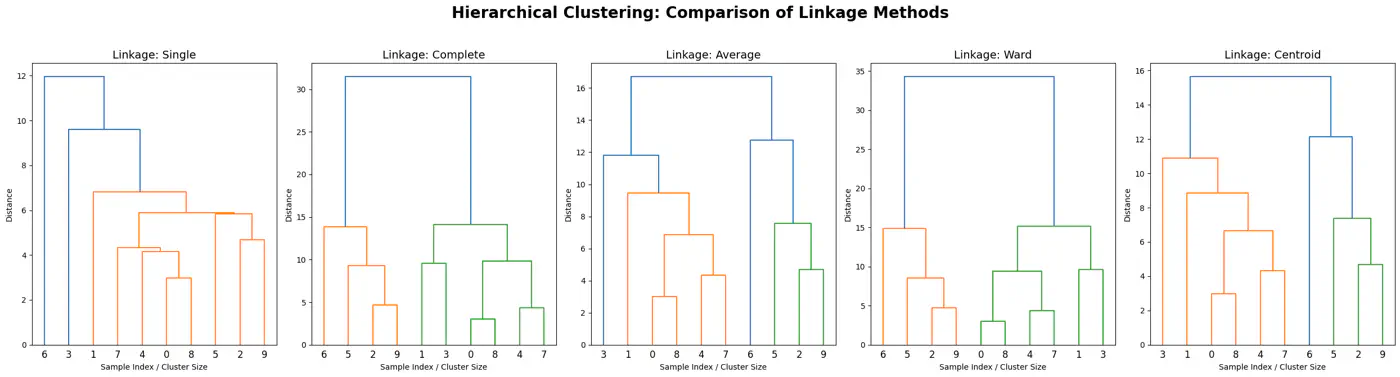
Closeness of Clusters
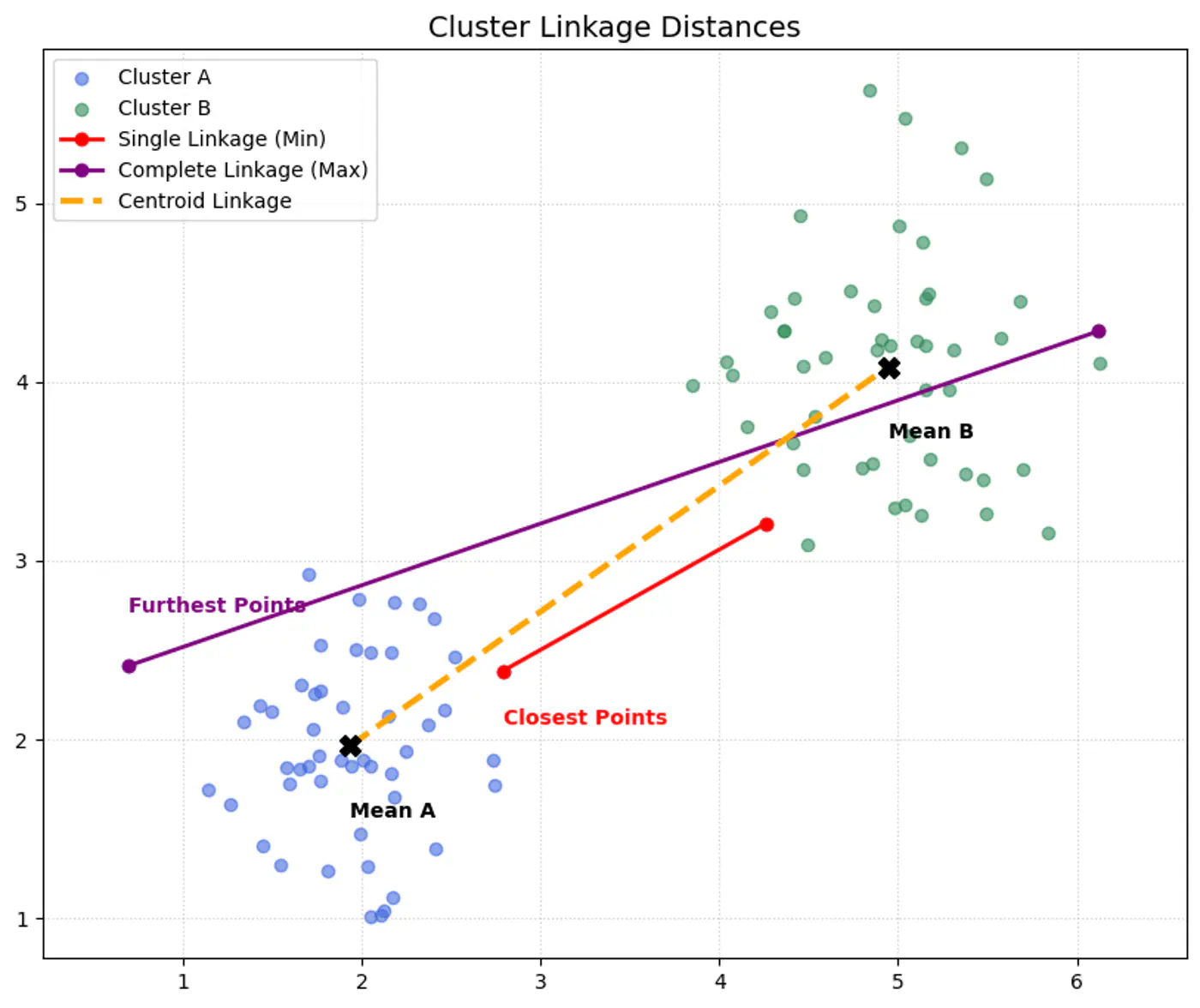
- Ward’s Method:
- Merges clusters to minimize the increase in the total within-cluster variance (sum of squared errors), resulting in compact, equally sized clusters.
- Single Linkage (MIN):
- Uses the minimum distance between any two points in different clusters.
- Prone to creating long, ‘chain-like’ 🔗 clusters, sensitive to outliers.
- Complete Linkage (MAX):
- Uses the maximum distance between any two points in different clusters.
- Forms tighter, more spherical clusters, less sensitive to outliers than single linkage.
- Average Linkage:
- Combines clusters by the average distance between all points in two clusters, offering a compromise between single and complete linkage.
- A good middle ground, often overcoming limitations of single and complete linkage.
- Centroid Method:
- Merges clusters based on the distance between their centroids (mean points).
👉Single Linkage is more sensitive to outlier than Complete Linkage, as Single Linkage can keep linking to the closest point forming a bridge to outlier.
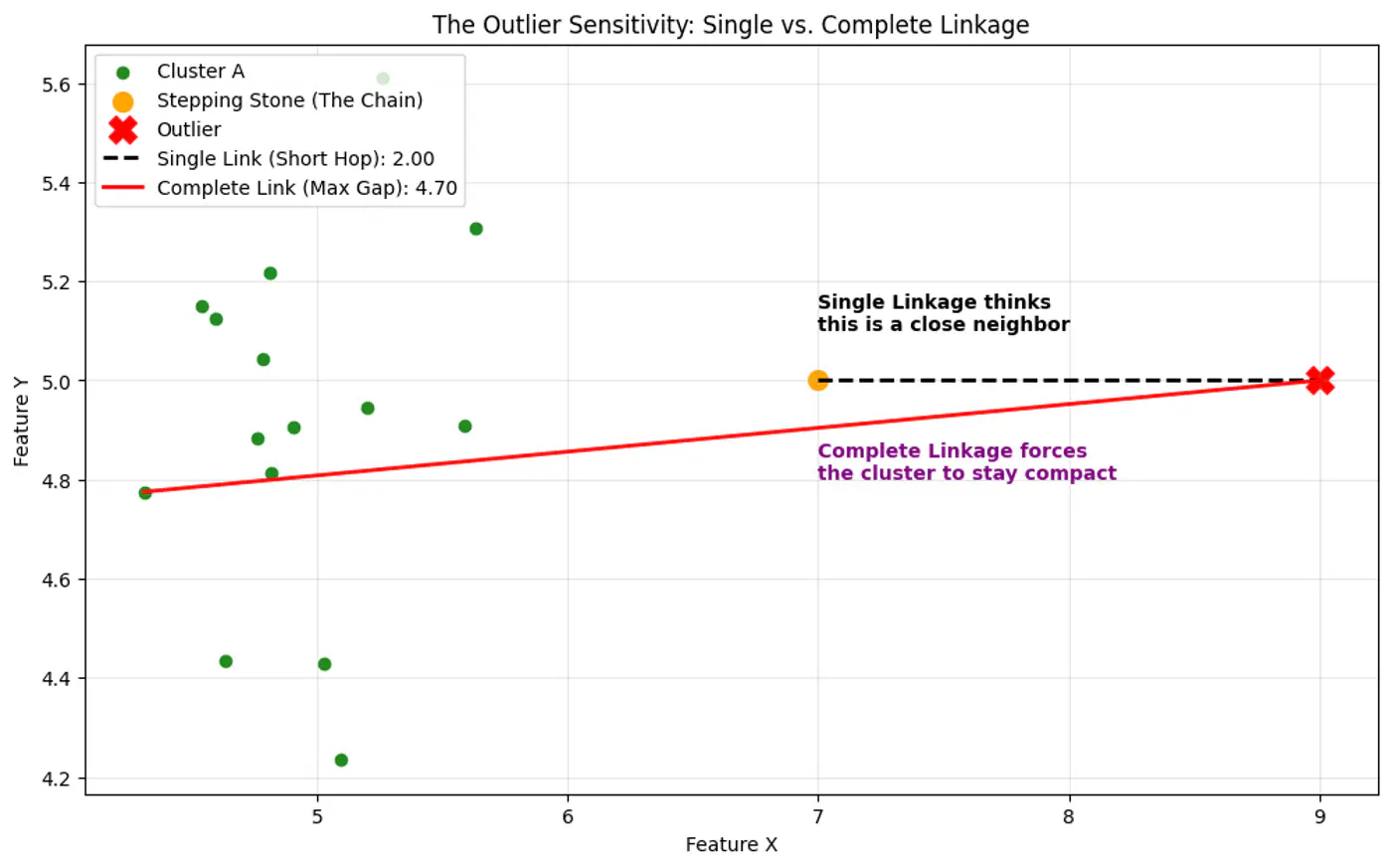
👉All cluster linkage distances.
👉We get different clustering using different linkages.
End of Section