Maths for AI & ML
This sheet contains all the topics that will be covered for Maths for AI & ML.
This is the multi-page printable view of this section. Click here to print.
This sheet contains all the topics that will be covered for Maths for AI & ML.
This sheet contains all the topics that will be covered for Probability for AI & ML.
For example:
\(P(\Omega) = 1\)
graph TD
A[Sample Space] --> |Discrete| B(Finite)
A --> C(Infinite)
C --> |Discrete| D(Countable)
C --> |Continuous| E(Uncountable)For example:
Note: If we know that event \(A\) has occurred, then we can say for sure that the event \(B\) did NOT occur.
For example:
Note: If we know that event \(A\) has occurred, then that gives us NO new information about the event \(B\).
Let’s understand this answer with an example.
Probability of choosing exactly one point on the number line or a real number, say 2.5,
from the interval \([2,3]\) is almost = 0, because there are infinitely many points between 2 and 3.
Also, we can NOT say that choosing exactly 2.5 is impossible, because it exists there on the number line.
But, for all practical purposes, \(P(2.5) = 0\).
Therefore, we say that \(P=0\) means “Highly Unlikely” and NOT “Impossible”.
Extending this line of reasoning, we can say that probability of NOT choosing 2.5, \(P(!2.5) = 1\).
Theoretically yes, because there are infinitely many points between 2 and 3.
But, we cannot say for sure that we cannot choose 2.5 exactly.
There is some probability of choosing 2.5, but it is very small.
Therefore, we say that \(P=1\) means “Almost Sure” and NOT “Certain”.
Here, in this case we can say that \(P(7)=0\) and that means Impossible.
Similarly, we can say that \(P(get ~any ~number ~between ~1 ~and ~6)=1\) and \(P=1 => \) Certain.
End of Introduction
Conditional Probability:
It is the probability of an event occurring, given that another event has already occurred.
Allows us to update probability when additional information is revealed.
For example:
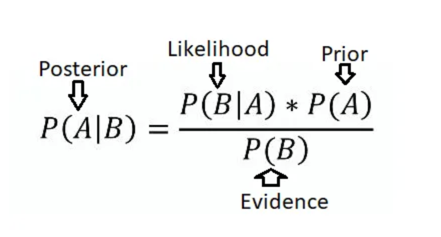
Bayes’ Theorem:
It is a formula that uses conditional probability.
It allows us to update our belief about an event’s probability based on new evidence.
We know from conditional probability and chain rule that:
Combining all the above equations gives us the Bayes’ Theorem:
$$ \begin{aligned} P(A \mid B) = \frac{P(A)*P(B \mid A)}{P(B)} \end{aligned} $$
For example:
\(P(B \mid A) = 1\) = Probability of getting an odd number given that we have rolled a 5.
Now, let’s understand another concept called Law of Total Probability.
Here, we can say that the sample space \(\Omega\) is divided into 2 parts - \(A\) and \(A ^ \complement \)
So, the probability of an event \(B\) is given by:
$$ B = B \cap A + B \cap A ^ \complement \\ P(B) = P(B \cap A) + P(B \cap A ^ \complement ) \\ By ~Chain ~Rule: P(B) = P(A)*P(B \mid A) + P(A ^ \complement )*P(B \mid A ^ \complement ) $$Law of Total Probability:
Overall probability of an event B, considering all the different, mutually exclusive ways it can occur.
If A₁, A₂, …, Aₙ are a set of events that partition the sample space, such that they are -
Now, we can also generalize the Bayes’ Theorem using the Law of Total Probability.
End of Section
Independence of Events:
Two events are independent if the occurrence of one event does not affect the probability of the other event.
There are 3 types of independence of events:
Mutual Independence:
Joint probability of two events is equal to the product of the individual probabilities of the two events.
\(P(A \cap B) = P(A)*P(B)\)
Joint probability: The probability of two or more events occurring simultaneously.
\(P(A \cap B)\) or \(P(A, B)\)
For example:
=> A and B are mutually independent.
For example:
Now, pair-wise independence of the above events A & B is - \(P(A \cap B)\)
\(P(A \cap B)\) => Outcomes of first and second toss are same &
outcomes of second and third toss are same.
=> Outcomes of all the three tosses are same.
Total number of outcomes = 8
Desired outcomes = \(\{HHH, TTT\}\) = 2
=> \(P(A \cap B) = 2/8 = 1/4 = P(A) * P(B) = 1/2 * 1/2 = 1/4\)
Therefore, \(A\) and \(B\) are pair-wise independent.
Similarly, we can also prove that \(A\) and \(C\) and \(B\) and \(C\) are also pair-wise independent.
Now, let’s check for mutual independence of the above events A, B & C.
\(P(A \cap B \cap C) = P(A)*P(B)*P(C)\)
\(P(A \cap B \cap C)\) = Outcomes of all the three tosses are same i.e \(\{HHH, TTT\}\)
Total number of outcomes = 8
Desired outcomes = \(\{HHH, TTT\}\) = 2
So, \(P(A \cap B \cap C)\) = 2/8 = 1/4
But, \(P(A)*P(B)*P(C) = 1/2*1/2*1/2 = 1/8\)
Therefore \(P(A \cap B \cap C)\) ≠ \(P(A)*P(B)*P(C)\)
=> \(A, B, C\) are NOT mutually independent but only pair wise independent.
=> A & B are NOT independent.
Now, let’s check for conditional independence of A & B given C.
Therefore, A & B are conditionally independent given C.
End of Section
Depending upon the nature of output, random variables are of 2 types - Discrete and Continuous.
Now, that we have understood that how random variable can be used to map outcomes of abstract random experiment to real
values for mathematical analysis, we will understand its applications.
2. Continuous random variable - Consider a line segment/interval from \(\Omega = [0,2] \)
Random variable \(X(\omega) = \omega\)
i.e \(X(1) = 1 ~and~ X(1.1) = 1.1 \)
End of Section

Binomial Distribution:
It extends the Bernoulli distribution by modeling the number of successes that occur over a fixed number of
independent trials.
n = Number of trials
k = Number of successes
p = Probability of success
Mean = np
Variance = np(1-p)
\(PMF, P(x=k) = \binom{n}{k}p^k(1-p)^{n-k}\), where \(k \in \{0,1,2,3,...,n\}\)
\(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) i.e number of ways to achieve ‘k’ successes in ‘n’ independent trials.
Note: Bernoulli is a special case of Binomial distribution where n = 1.
Also read about Multinomial distribution i.e where number of possible outcomes is > 2.
Total number of outcomes in 3 coin tosses = 2^3 = 8
Desired outcomes i.e 2 heads in 3 coin tosses = \(\{HHT, HTH, THH\}\) = 3
Probability of getting exactly 2 heads in 3 coin tosses = \(\frac{3}{8}\) = 0.375
Now lets solve the question using the binomial distribution formula.
Number of successes, k = 1
Number of trials, n = 10
Probability of success, p = 1/3
Probability of winning lottery, P(k=1) =
Poisson Distribution:
It expresses the probability of an event happening a certain number of times ‘k’ within a fixed interval of time.
Given that:
PMF = Probability of occurrence of ‘k’ events in the same interval
Note: Useful to count data where total population size is large but the probability of an individual event is small.
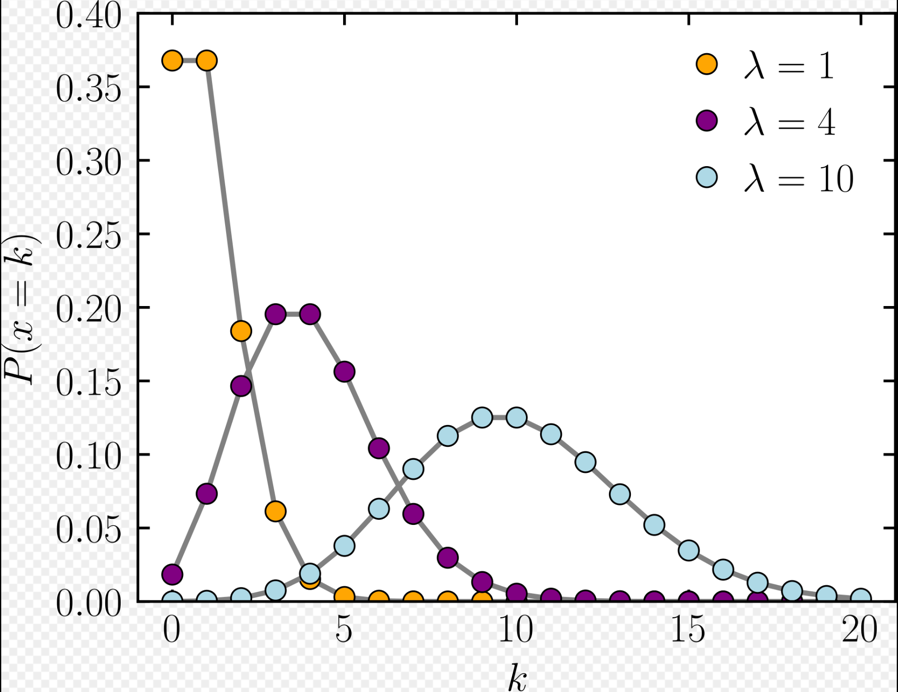
Expected (average) number of emails per hour, \(\lambda\) = 5
Probability of receiving exactly k=3 emails in the next hour =
End of Section
Probability Density Function(PDF):
This is a function used for continuous random variables to describe the likelihood of the variable taking on a value
within a specific range or interval.
Since, at any given point the probability of a continuous random variable is zero,
we find the probability within a given range.
Note: Called ‘density’ because probability is spread continuously over a range of values
rather than being concentrated at a single point as in PMF.
e.g: Uniform, Gaussian, Exponential, etc.
Note: PDF is a continuous function \(f(x)\).
It is also the derivative of Cumulative Distribution Function (CDF) \(F_X(x)\)
\(PDF = f(x) = F'(X) = \frac{dF_X(x)}{dx} \)
For example:
Consider a line segment/interval from \(\Omega = [0,2] \)
Random variable \(X(\omega) = \omega\)
i.e \(X(1) = 1 ~and~ X(1.1) = 1.1 \)
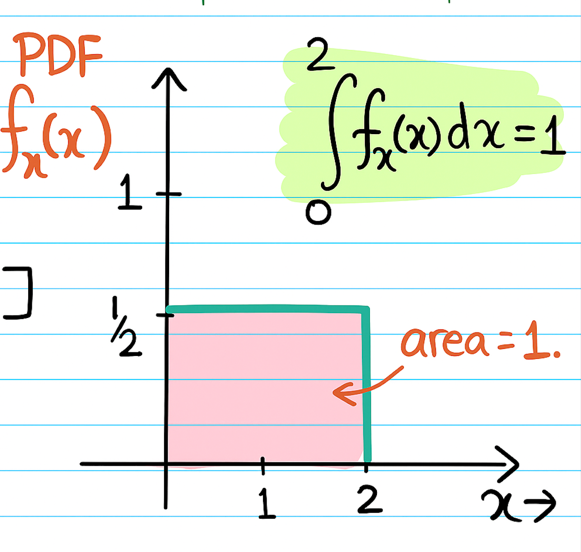
Note: If we know the PDF of a continuous random variable, then we can find the probability of any given region/interval
by calculating the area under the curve.
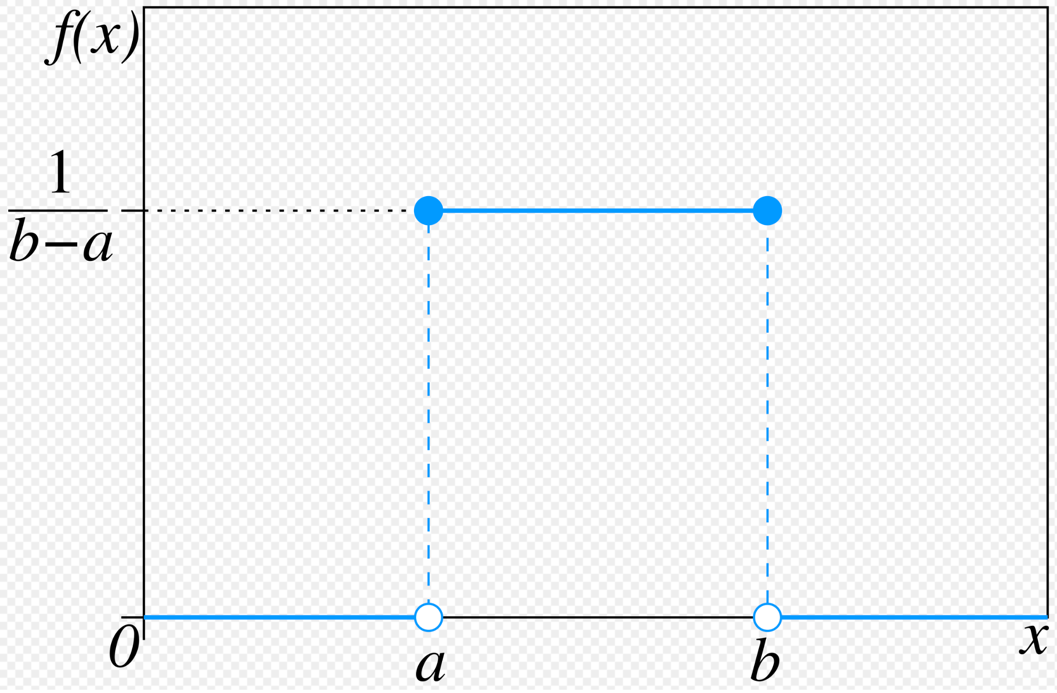
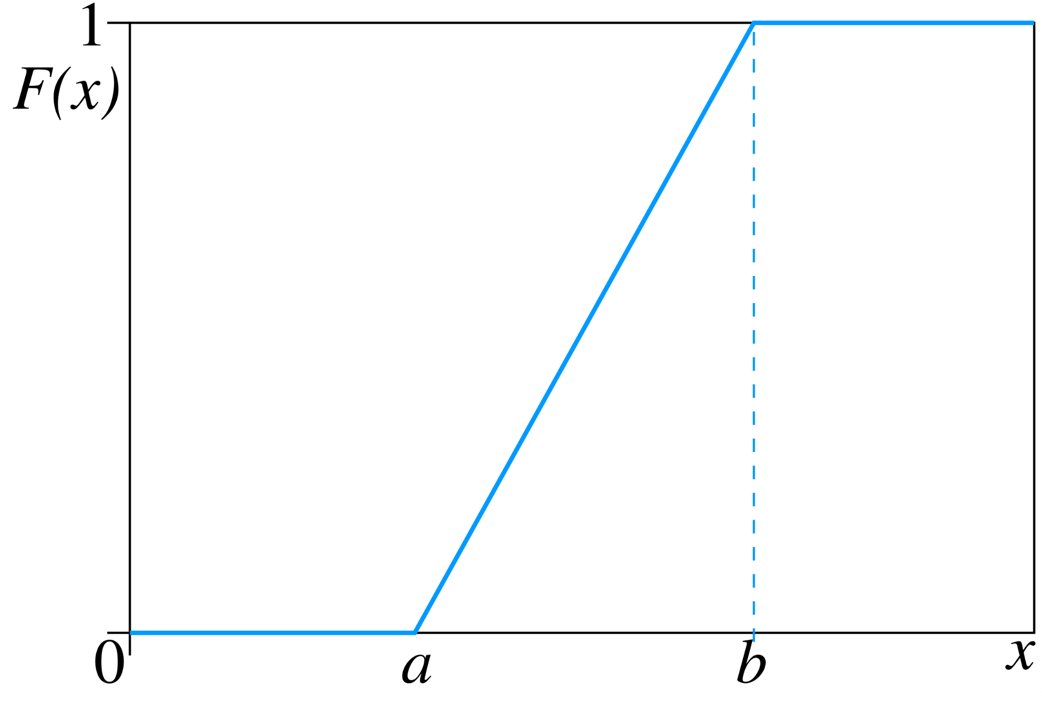
Uniform Distribution:
All the outcomes within the given range are equally likely to occur.
Also known as ‘fair’ distribution.
Note: This is a natural starting point to understand randomness in general.
Mean = Median = \( \frac{a+b}{2} ~if~ x \in [a,b] \)
Variance = \( \frac{(b-a)^2}{12} \)
Standard uniform distribution: \( X \sim U(0,1) \)
PDF in terms of mean(\(\mu\)) and standard deviation(\(\sigma\)) -
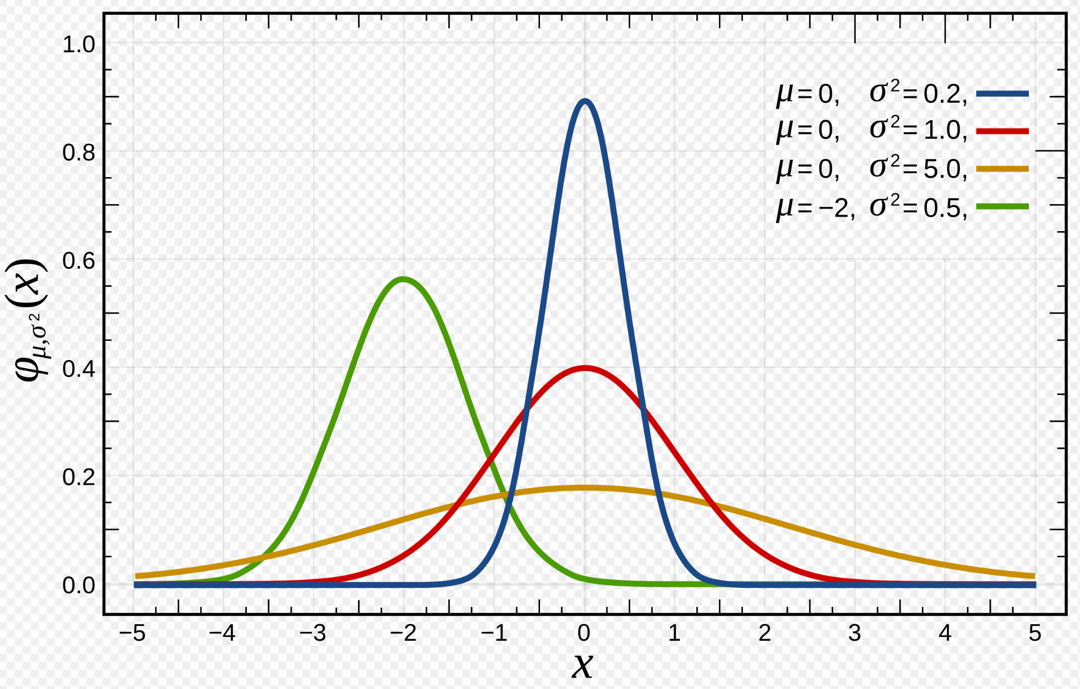
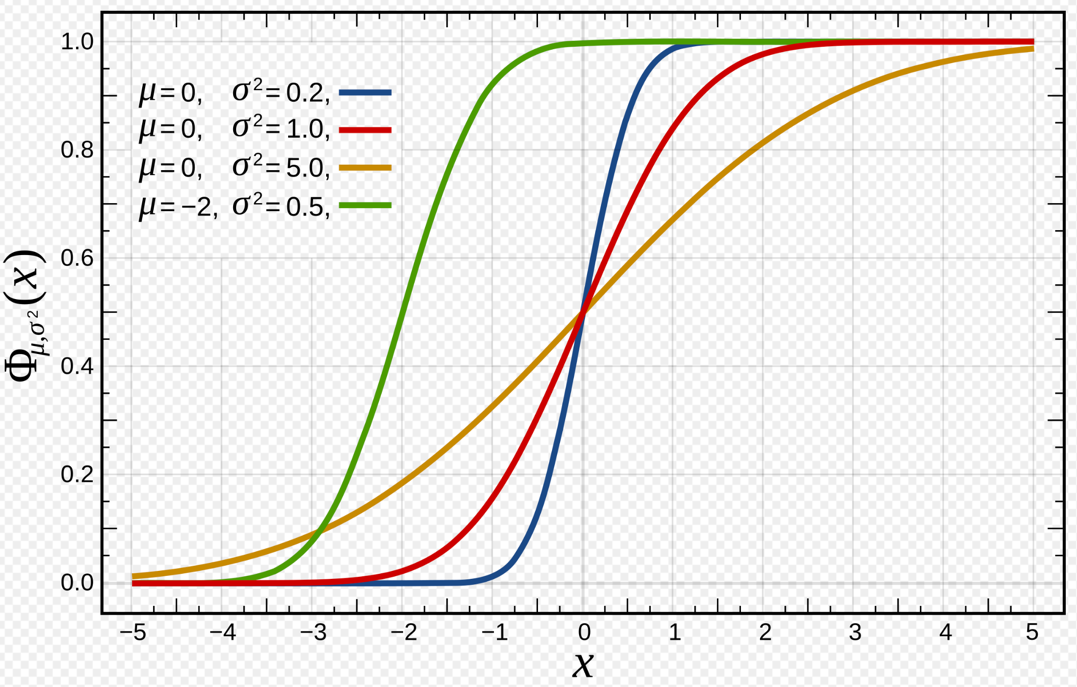
Gaussian(Normal) Distribution:
It is a continuous probability distribution characterized by a symmetrical, bell-shaped curve with
most data clustered around the central average, with frequency of values decreasing as they move away from the center.
Standard normal distribution:
\[ Z \sim N(0,1) ~i.e~ \mu = 0, \sigma^2 = 1 \]
Any normal distribution can be standardized using Z-score transformation:
For example:
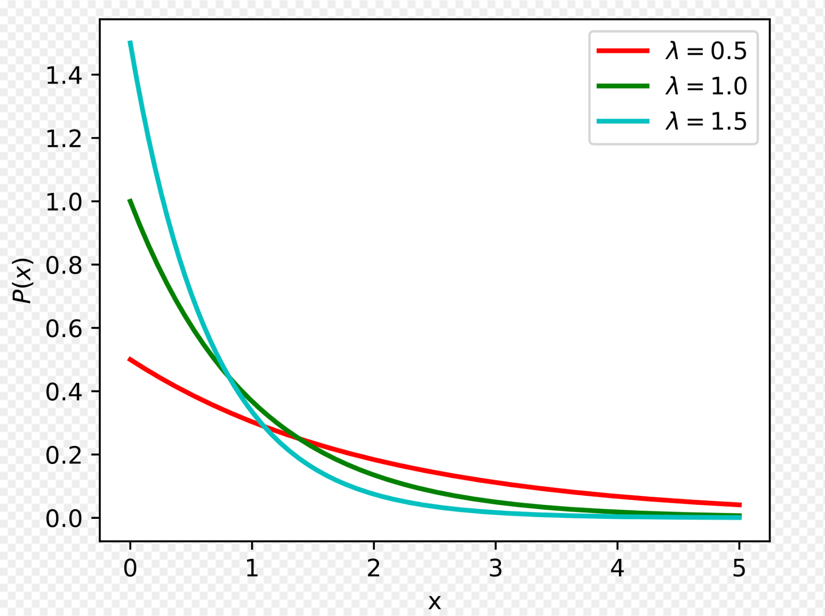
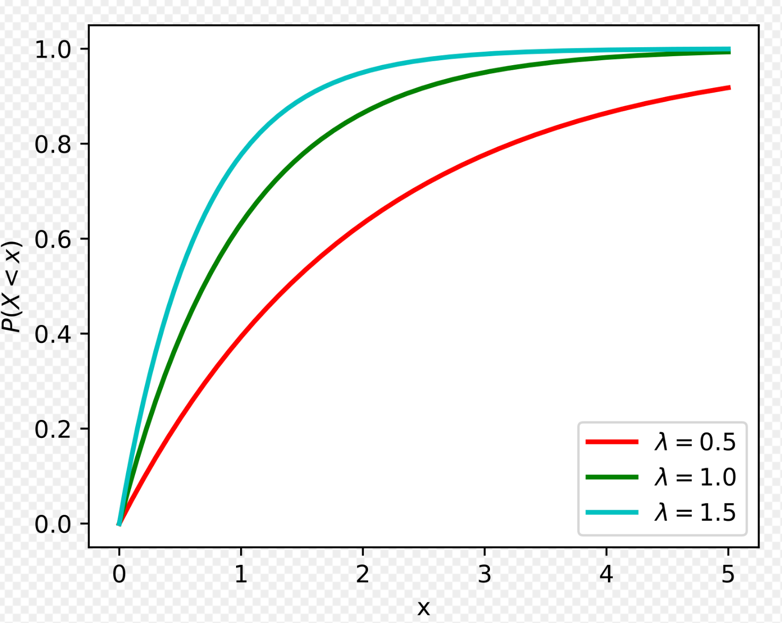
Exponential Distribution:
It is used to model the amount of time until a specific event occurs.
Given that:
Mean time to serve 1 customer = \(\mu\) = 4 minutes
So, \(\lambda\) = average number of customers served per unit time = \(1/\mu\) = 1/4 = 0.25 minutes
Probability to serve a customer in less than 3 minutes can be found using CDF -
So, probability of a customer being served in less than 3 minutes is 53%(approx).
In this case x = 2 minutes, and \(\lambda\) = 0.25 so,
So, probability of a customer being served in greater than 2 minutes is 60%(approx).
Probability of waiting for an additional period of time for an event to occur is independent of
how long you have already waited.
e.g: Lifetime of electronic items follow exponential distribution.
Note: Memoryless property makes exponential distribution particularly useful for -
Task: We want to find the probability of the electronic item lasting for \(x > t+s \) days,
given that it has already lasted for \(x>t\) days.
This is a ‘conditional probability’.
Since,
We want to find: \( P(X > t+s \mid X > t) = ~? \)
Hence, probability that the electronic item will survive for an additional time ’s’ days
is independent of the time ’t’ days it has already survived.
Poisson distribution models the number of events occurring in a fixed interval of time,
given a constant average rate \(\lambda \).
Exponential distribution models the time interval between those successive events.
Note: If the number of events in a given interval follow a Poisson distribution, then the waiting time between those events will necessarily follow an Exponential distribution.
Lets see the proof for the above statement.
Poisson Case:
The probability of observing exactly ‘k’ events in a time interval of length ’t’
with an average rate of \( \lambda \) events per unit time is given by -
The event that waiting time until next event > t, is same as observing ‘0’ events in that interval.
=> We can use the PMF of Poisson distribution with k=0.
Exponential Case:
Now, lets consider exponential distribution that models the waiting time ‘T’ until next event.
The event that waiting time ‘T’ > t, is same as observing ‘0’ events in that interval.
Observation:
Exponential distribution is a direct consequence of Poisson distribution probability of ‘0’ events.
Using Poisson:
Average failure rate, \(\lambda\) = 1/20 = 0.05
Time interval, t = 10 hours
Number of events, k = 0
Average number of events in interval, (\(\lambda t\)) = (1/20) * 10 = 0.5
Probability of having NO failures in the next 10 hours = ?
Using Exponential:
What is the probability that wait time until next failure > 10 hours?
Waiting time, T > t = 10 hours.
Average number of failures per hour, \(\lambda\) = 1/20 per hour
Therefore, we have seen that this problem can be solved using both Poisson and Exponential distribution.
End of Section
Expectation:
Long run average of the outcomes of a random experiment.
When we talk about ‘Expectation’ we mean - on an average.
Note: If the probability of each outcome is different, then we take a weighted average.
Discrete Case:
\(E[X] = \sum_{i=1}^{n} x_i.P(X = x_i) \)
Continuous Case:
\(E[X] = \int_{-\infty}^{\infty} x.f(x) dx \)
Possible outcomes are: \(x_1 = 100 ,~ x_2 = -50 \)
Probability of each outcome is \(P(X = 100) = 0.5,~ P(X = -50) = 0.5 \)
Therefore, the expected value of the amount that you will win per toss is Rs. 25 in the long run.
Variance:
It is the average of the squared differences from the mean.
Variance in terms of expected value, where \(E[X] = \mu\), is given by:
\[ \begin{aligned} Var[X] &= E[(X - E[X])^2] \\ &= E[X^2 + E[X]^2 - 2XE[X]] \\ &= E[X^2] + E[X]^2 - 2E[X]E[X] \\ &= E[X^2] + E[X]^2 - 2E[X]^2 \\ Var[X] &= E[X^2] - E[X]^2 \\ \end{aligned} \]Note: This is the computational formula for variance, as it is easier to calculate than the
average of square distances from mean.
PDF of continuous uniform random variable =
$$ \begin{aligned} f_X(x) &= \begin{cases} \dfrac{1}{b-a}, & x \in [a,b] \\ 0, & \text{otherwise.} \end{cases} \\ \end{aligned} $$\[ \begin{aligned} \text{Expected value = mean } = \\[0.5em] E[X] = \dfrac{b+a}{2} \\[0.5em] Var[X] = E[X^2] - E[X]^2 \end{aligned} \]We know \(E[X]\) already, now we will calculate \(E[X^2]\):
\[ \begin{aligned} E[X] &= \int_{-\infty}^{\infty} x.f(x) dx \\ E[X^2] &= \int_{-\infty}^{\infty} x^2.f(x) dx \\ &= \int_{-\infty}^{a} x^2f(x) dx + \int_{a}^{b} x^2f(x) dx + \int_{b}^{\infty} x^2f(x) dx\\ &= 0 + \int_{a}^{b} x^2f(x) dx + 0 \\ &= \int_{a}^{b} x^2f(x) dx \\ &= \dfrac{1}{b-a} \int_{a}^{b} x^2 dx \\ &= \dfrac{1}{b-a} * \{\frac{x^3}{3}\}_{a}^{b} \\ &= \dfrac{1}{b-a} * \{\frac{b^3 - a^3}{3}\} \\ &= \dfrac{1}{b-a} * \{\frac{(b-a)(b^2+ab+a^2)}{3}\} \\ E[X^2] &= \dfrac{b^2+ab+a^2}{3} \end{aligned} \]Now, we know both \(E[X]\) and \(E[X^2]\), so we can calculate \(Var[X]\):
\[ \begin{aligned} Var[X] &= E[X^2] - E[X]^2 \\ &= \dfrac{b^2+ab+a^2}{3} - \dfrac{(b+a)^2}{4} \\ &= \dfrac{b^2+ab+a^2}{3} - \dfrac{b^2+2ab+a^2}{4} \\ &= \dfrac{4b^2+4ab+4a^2-3b^2-6ab-3a^2}{12} \\ &= \dfrac{b^2-2ab+a^2}{12} \\ Var[X]&= \dfrac{(b-a)^2}{12} \end{aligned} \]Co-Variance:
It is the measure of how 2 variables X & Y vary together.
It gives the direction of the relationship between the variables.
Note: For both direction as well as magnitude, we use Correlation.
Let’s use expectation to compute the co-variance of two random variables X & Y:
Note:
End of Section
Moments:
They are statistical measures that describe the characteristics of a probability distribution,
such as its central tendency, spread/variability, and asymmetry.
Note: We will discuss ‘raw’ and ‘central’ moments.
Important moments:
Moment Generating Function:
It is a function that simplifies computation of moments, such as, the mean, variance, skewness, and kurtosis,
by providing a compact way to derive any moment of a random variable through differentiation.
Not all probability distributions have MGFs; sometimes, integrals may not converge and moment may not exist.
Since, \(MGF = M_X(t) = E[e^{tX}] \), we can write the MGF as:
Say, \( E[X^n] = m_n \), where \(m_n\) is the \(n^{th}\) moment of the random variable, then:
\[ M_X(t) = 1 + \frac{t}{1!}m_1 + \frac{t^2}{2!}m_2 + \frac{t^3}{3!}m_3 + \cdots + \frac{t^n}{n!}m_n + \cdots \\ \]Important: Differentiating \(M_X(t)\) with respect to \(t\), \(i\) times, and setting \((t =0)\) gives us the \(i^{th}\) moment of the random variable.
\[ \frac{dM_X(t) }{dt} = M'_X(t) = 0 + m_1 + \frac{2t}{2!}m_2 + \frac{3t^2}{3!}m_3 + \cdots + \frac{nt^n-1}{n!}m_n + \cdots \\ \]Set \(t=0\), to get the first moment:
\[ \frac{dM_X(t) }{dt} = M'_X(t) = m_1 \]Similarly, second moment = \(M''_X(t) = m_2 = E[X^2]\)
And, \(n^{th}\) derivative = \(M^{(n)}_X(t) = m_n = E[X^n]\)
e.g: \( Var[X] = M''_X(0) - (M'_X(0))^2 \)
Note: If we know the MGF of a random variable, then we do NOT need to do integration or summation to find the moments.
Continuous:
Discrete:
\[ M_X(t) = E[e^{tX}] = \sum_{i=1}^{\infty} e^{tx} P(X=x) \]End of Section
Joint Probability Distribution:
It describes the probability of 2 or more random variables occurring simultaneously.
Joint CDF:
Discrete Case:
Continuous Case:
Joint PMF:
Key Properties:
Joint PDF:
Key Properties:
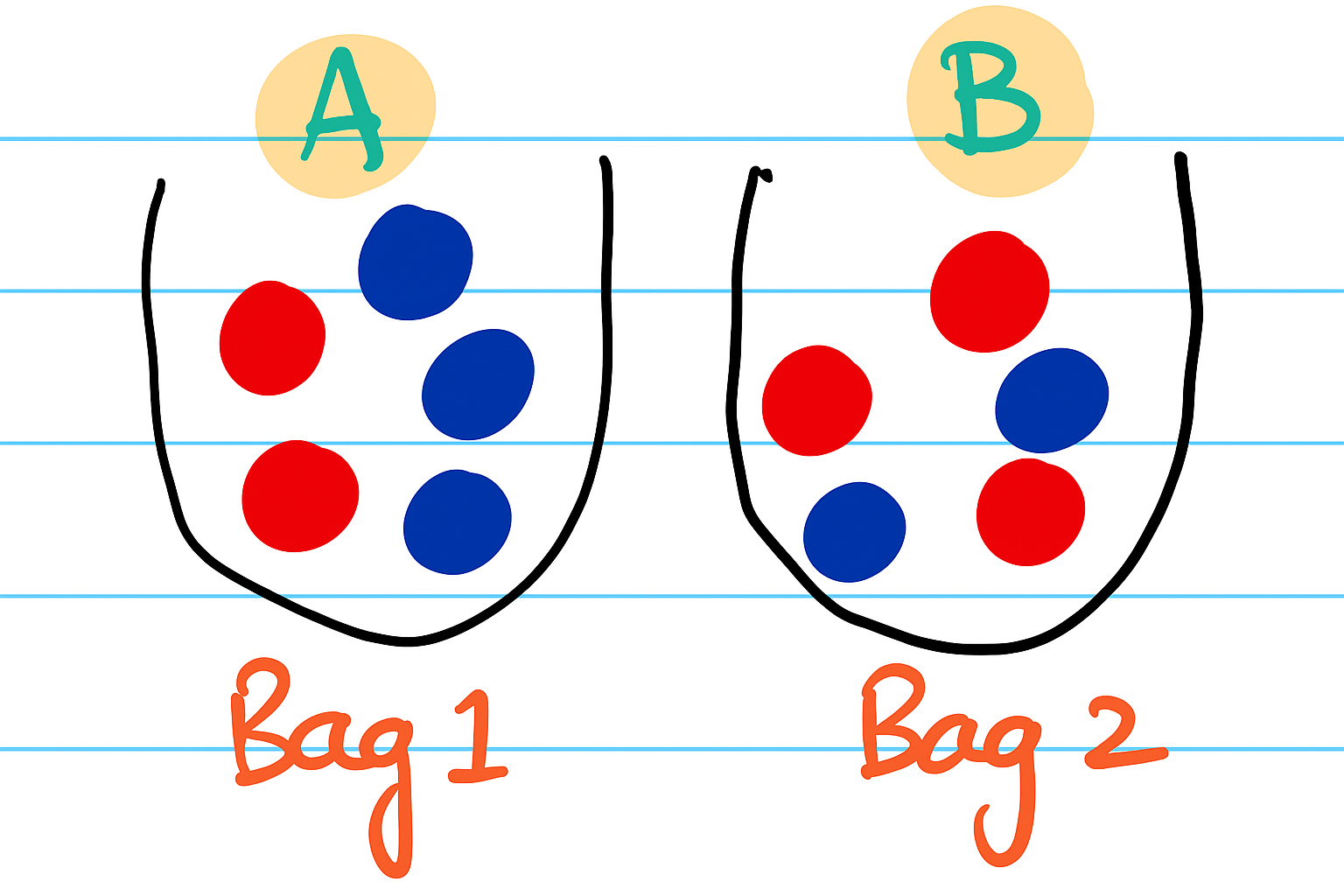
Let A & B be discrete random variables associated with the outcome of the ball drawn from first and second bags
respectively.
| A = Red | A = Blue | |
|---|---|---|
| B = Red | 2/5*3/5 = 6/25 | 3/5*3/5 = 9/25 |
| B = Blue | 2/5*2/5 = 4/25 | 3/5*2/5 = 6/25 |
Since, the draws are independent, joint probability = P(A) * P(B)
Each of the 4 cells in above table shows the probability of combination of results from 2 draws or joint probability.
Marginal Probability Distribution:
It describes the probability distribution of an individual random variable in a joint distribution,
without considering the outcomes of other random variables.
Marginal CDF:
We know that Joint CDF =
Marginal CDF =
\[ F_X(a, \infty) = P(X \le a, Y < \infty) = P(X \le a) \]Discrete Case:
Continuous Case:
Law of Total Probability
We know that Joint Probability Distribution =
The events \((Y=y)\) partition the sample space, such that:
From Law of Total Probability, we get:
Marginal PMF:
Marginal PDF:
Joint PMF = \( P_{X,Y}(x,y) = P(X=x, Y=y) = 1/6*1/2 = 1/12\)
Marginal PMF of X = \( P_X(x) =\sum_{y \in \mathbb{\{H,T\}}} P_{X,Y}(x,y) = = 1/12+1/12 = 1/6\)
=> Marginally, X is uniform over 1-6 i.e a fair die.
Marginal PMF of Y = \( P_Y(y) = \sum_{1}^6 P_{X,Y}(x,y) = 6*(1/12) = 1/2 \)
=> Marginally, Y is uniform over H,T i.e a fair coin.
Marginal PDF = \(f_X(x) = \int_{-\infty}^{\infty} f_{X,Y}(x,y) dy \)
Joint PDF =
Marginal PDF =
\[ \begin{aligned} f_X(x) &= \int_{0}^{1} f_{X,Y}(x,y) dy \\ &= \int_{0}^{1} 1 dy \\ &= 1 \\ f_X(x) &= \begin{cases} 1 & \text{if } x \in [0,1] \\ 0 & \text{otherwise } \end{cases} \end{aligned} \]
Let A & B be discrete random variables associated with the outcome of the ball drawn from first and second bags
respectively.
| A = Red | A = Blue | P(B) (Marginal) | |
|---|---|---|---|
| B = Red | 2/5*3/5 = 6/25 | 3/5*3/5 = 9/25 | 6/25 + 9/25 = 15/25 = 3/5 |
| B = Blue | 2/5*2/5 = 4/25 | 3/5*2/5 = 6/25 | 4/25 + 6/25 = 10/25 = 2/5 |
| P(A) (Marginal) | 6/25 + 4/25 = 10/25 = 2/5 | 9/25 + 6/25 = 15/25 = 3/5 |
We can see from the table above - P(A=Red) is the sum of joint distribution over all possible values of B i.e Red & Blue.
Conditional Probability:
It measures the probability of an event occurring given that another event has already happened.
P(A, B) = Joint Probability of A and B
P(B) = Marginal Probability of B
=> Conditional Probability = Joint Probability / Marginal Probability
Conditional CDF:
Discrete Case:
Continuous Case:
Conditional PMF:
Conditional PDF:
Application:

Let A & B be discrete random variables associated with the outcome of the ball drawn from first and second bags
respectively.
A = Red ball in first draw
B = Blue ball in second draw.
| A = Red | A = Blue | P(B) (Marginal) | |
|---|---|---|---|
| B = Red | 6/25 | 9/25 | 3/5 |
| B = Blue | 4/25 | 6/25 | 2/5 |
| P(A) (Marginal) | 2/5 | 3/5 |
Therefore, probability of drawing a red ball in the first draw, given that a blue ball is drawn in second draw = 2/5.
Conditional Expectation:
This gives us the conditional expectation of a random variable X, given another random variable Y=y.
Discrete Case:
Continuous Case:
For example:
Applications:
Conditional Variance:
This gives us the variance of a random variable calculated after taking into account the value(s) of another related variable.
For example:
Note: Models that take into account the change in variance or heteroscedasticity tend to be more accurate.
End of Section
There are 2 parts in I.I.D, “Independent” and “Identically Distributed”.
Let’s revisit and understand the independence of random variables first.
Independence of Random Variables
It means that the knowing the outcome of one random variable does not impact the probability of the other random variable.
Two random variables X & Y are independent if:
Here, clearly, X and Y are independent.
X, Y are NOT independent, but mutually exclusive, because if we know about one, then we automatically know about the other.
Let’s check for independence of \(X\) and \(Y\) i.e \(E[XY] = E[X]E[Y]\) or not?
Now, lets calculate the value of \(E[XY]\):
From (1) and (2), we can say that:
\[ E[XY] ⍯ E[X]E[Y] \\ \]Hence, \(X\) and \(Y\) are NOT independent.
Read more about Integration
Independent & Identically Distributed(I.I.D)
I.I.D assumption for samples(data points) in a dataset means that the samples are:
End of Section
Convergence in Probability:
A sequence of random variables \(X_1, X_1, \dots, X_n\) is said to converge in probability
to a known random variable \(X\),
if for every number \(\epsilon >0 \), the following is true:
where,
\(X_n\): is the estimator or sample based random variable.
\(X\): is the known or limiting or target random variable.
\(\epsilon\): is the tolerance level or margin of error.
For example:
Say, tolerance level \(\epsilon = 0.1\).
Then,
If n=5;
So, if n=5, then \(|X_n - X| > (\epsilon = 0.1)\).
=> \(P(|X_n - X| \ge (\epsilon=0.1)) = 1\).
if n=20;
So, if n=20, then \(|X_n - X| < (\epsilon=0.1)\).
=> \(P(|X_n - X| \ge (\epsilon=0.1)) = 0\).
=> \(P(|X_n - X| \ge (\epsilon=0.1)) = 0 ~\forall ~n \ge 10\)
Therefore,
Similarly, we can prove that if \(\epsilon = 0.01\), then the probability will be equal to 0 for \( n\ge 100 \).
Note: Task is to check whether the sequence of randome variables \(X_1, X_2, \dots, X_n\) converges in probability to a known random variable \(X\) as \(n\rightarrow\infty\).
So, we can conclude that, if \(n > \frac{1}{\epsilon}\), then:
Almost Sure Convergence:
A sequence of random variables \(X_1, X_2, \dots, X_n\) is said to almost surely converge to a known random variable \(X\),
for \(n \ge 1\), if the following is true:
where,
\(X_n\): is the estimator or sample based random variable.
\(X\): is the known or limiting or target random variable.
If, \(X_n \xrightarrow{Almost ~ Sure} X \), => \(X_n \xrightarrow{Probability} X \)
But, converse is NOT true.
*Note: Almost Sure convergence is hardest to satisfy amongst all convergence, such as, convergence in probability,
convergence in distribution, etc.
Read more about Limits
End of Section
Weak Law of Large Numbers (WLLN):
This law states that given a sequence of independent and identically distributed (IID) samples \(X_1, X_1, \dots, X_n\)
from a random variable with finite mean, the sample mean (\(\bar{X_n}\)) converges in probability to
the expected value \(E[X]\) or population mean (\( \mu \)).
Note: Does NOT guarantee that sample mean will be close to population mean,
but instead says that - the probability of sample mean being far away from the population mean is low.
Read more about Limits
Strong Law of Large Numbers (SLLN):
This law states that given a sequence of independent and identically distributed (IID) samples \(X_1, X_1, \dots, X_n\)
from a random variable with finite mean, the sample mean (\(\bar{X_n}\)) converges almost surely to
the expected value \(E[X]\) or population mean (\( \mu \)).
Note:
Application:
End of Section
Markov’s Inequality:
It gives an upper bound for the probability that a non-negative random variable will NOT exceed, based on its expected value.
Note: It gives a very loose upper bound.
Read more about Expectation
Hence, a 25% chance of serving more than 200 customers.
Hence, there is a 78% chance that a randomly selected student gets a score of 90 marks or more.
Chebyshev’s Inequality:
It states that the probability of a random variable deviating from its mean is small if its variance is small.
Note: It gives a tighter upper bound than Markov’s Inequality.
Given, the standard deviation of the test score \(\sigma\) = 10 marks.
=> Variance = \(\sigma^2\) = 100
Hence, Chebyshev’s Inequality gives a far tighter upper bound of 25% than Markov’s Inequality of 78%(approx).
Chernoff Bound:
It is an upper bound on the probability that a random variable deviates from its expected value.
It’s an exponentially decreasing bound on the “tail” of a random variable’s distribution,
which can be calculated using its moment generating function.
Proof:
For the sum of ’n’ independent random variables,
Note: Used to compute how far the sum of independent random variables deviate from their expected value.
Read more about Moment Generating Function
End of Section
Surprise Factor:
It is a measure of the amount of information gained when a specific, individual event occurs, and is defined based on
the probability of that event.
It is defined as the negative logarithm of the probability of the event.
Note: Logarithm(for base > 1) is a monotonically increasing function, so as x increases, log(x) also increases.
Units:
Entropy:
It conveys how much ‘information’ we expect to gain from a random event.
Case 1:
Toss a fair coin; \(P(H) = P(T) = 0.5 = 2^{-1}\)
Surprise factor (Heads or Tails) = \(-log(P(x)) = -log_2(0.5) = -log_2(2^{-1}) = 1~bit\)
Entropy = \( \sum_{x \in X} P(x)log(-P(x)) = 0.5*1 + 0.5*1 = 1 ~bit \)
Case 2:
Toss a biased coin; \(P(H) = 0.9 P(T) = 0.1 \)
Surprise factor (Heads) = \(-log(P(x)) = -log_2(0.9) \approx 0.15 ~bits \)
Surprise factor (Tails) = \(-log(P(x)) = -log_2(0.1) \approx 3.32 ~bits\)
Entropy = \( \sum_{x \in X} P(x)log(-P(x)) = 0.9*0.15 + 0.1*3.32 \approx 0.47 ~bits\)
Therefore, a biased coin is less surprising on an average than a fair coin, hence lower entropy.
Cross Entropy:
It is a measure of the average ‘information gain’ or ‘surprise’ when using an imperfect model \(Q\) to encode events
from a true model \(P\).
A model is trained to classify images as ‘cat’ or ‘dog’. Say, for an input image the true label is ‘cat’,
so the true distribution:
\(P = [1.0 ~(cat), 0.0 ~(dog)]\).
Let’s calculate the cross-entropy for the outputs of 2 models A & B.
Model A:
\(Q_A = [0.8 ~(cat), 0.2 ~(dog)]\)
Cross Entropy = \(H(P, Q_A) = -\sum_{i=1}^n P(x_i)log(Q_A(x_i)) \)
\(= -[1*log_2(0.8) + 0*log_2(0.2)] \approx 0.32 ~bits\)
Note: This is very low cross-entropy, since the predicted value is very close to actual, i.e low surprise.
Model B:
\(Q_B = [0.2 ~(cat), 0.8 ~(dog)]\)
Cross Entropy = \(H(P, Q_B) = -\sum_{i=1}^n P(x_i)log(Q_B(x_i)) \)
\(= -[1*log_2(0.2) + 0*log_2(0.8)] \approx 2.32 ~bits\)
Note: Here the cross-entropy is very high, since the predicted value is quite far from the actual truth, i.e high surprise.
Kullback Leibler (KL) Divergence:
It measures the information lost when one probability distribution \(Q\) is used to approximate another distribution \(P\).
It quantifies the ‘extra cost’ in bits needed to encode data using the approximate distribution \(Q\) instead of
the true distribution \(P\).
KL Divergence = Cross Entropy(P,Q) - Entropy(P)
\[ \begin{aligned} D_{KL}(P \parallel Q) &= H(P, Q) - H(P) \\ &= -\sum_{i=1}^n P(x_i)log(Q(x_i)) - [-\sum_{i=1}^n P(x_i)log(P(x_i))] \\[10pt] &= \sum_{i=1}^n P(x_i)[log(P(x_i)) - log(Q(x_i)) ] \\[10pt] D_{KL}(P \parallel Q) &= \sum_{i=1}^n P(x_i)log(\frac{P(x_i)}{Q(x_i)}) \\[10pt] \text{ For continuous case: } \\ D_{KL}(P \parallel Q) &= \int_{-\infty}^{\infty} p(x)log(\frac{p(x)}{q(x)})dx \end{aligned} \]Note:
Using the same cat, dog classification problem example as mentioned above.
A model is trained to classify images as ‘cat’ or ‘dog’. Say, for an input image the true label is ‘cat’,
so the true distribution:
\(P = [1.0 ~(cat), 0.0 ~(dog)]\).
Let’s calculate the KL divergence for the outputs of the 2 models A & B.
Let’s calculate entropy first, and we can reuse the cross-entropy values calculated above already.
Entropy: \(H(P) = -\sum_{x \in X} P(x)log(P(x)) = -[1*log_2(1) + 0*log_2(0)] = 0 ~bits\)
Note: \(0*log_2(0) = 0\), is an approximation hack, since \(log(0)\) is undefined.
Model A:
\( D_{KL}(P \parallel Q) = H(P, Q) - H(P) = 0.32 - 0 = 0.32 ~bits \)
Model A incurs an additional 0.32 bits of surprise due to its imperfect prediction.
Model B:
\( D_{KL}(P \parallel Q) = H(P, Q) - H(P) = 2.32 - 0 = 2.32 ~bits \)
Model B has much more ‘information loss’ or incurs higher ‘penalty’ of 2.32 bits as its prediction was from from the truth.
Jensen-Shannon Divergence:
It is a smoothed and symmetric version of the Kullback-Leibler (KL) divergence and is calculated by averaging the
KL divergences between each of the two distributions and their combined average distribution.
Let’s continue the cat and dog image classification example discussed above.
A model is trained to classify images as ‘cat’ or ‘dog’. Say, for an input image the true label is ‘cat’,
so the true distribution:
\(P = [1.0 ~(cat), 0.0 ~(dog)]\).
Step 1: Calculate the average distribution M.
Step 2: Calculate \(D_{KL}(P \parallel M)\).
Step 3: Calculate \(D_{KL}(Q \parallel M)\).
Step 4: Finally, lets put all together to calculate \(D_{JS}(P \parallel Q)\).
Therefore, lower JS divergence value => P and Q are more similar.
End of Section
Parametric Model Estimation:
It is the process of finding the best-fitting finite set of parameters \(\Theta\) for a model that assumes a
specific probability distribution for the data.
It involves using the dataset to estimate the parameters (like the mean and standard deviation of a normal distribution)
that define the model.
\(P(X \mid \Theta) \) : Probability of seeing data \(X: (X_1, X_2, \dots, X_n) \), given the parameters \(\Theta\) of the
underlying probability distribution from which the data is assumed to be generated.
Goal of estimation:
We observed data, \( D = \{X_1, X_2, \dots, X_n\} \), and we want to infer the the unknow parameters \(\Theta\)
of the underlying probability distribution, assuming that the data is generated I.I.D.
Read more for I.I.D
Note: Most of the time, from experience, we know the underlying probability distribution of data, such as, Bernoulli, Gaussian, etc.
Maximum Likelihood Estimation:
It is the most popular frequentist approach to estimate the parameters of a model.
This method helps us find the parameters \(\Theta\) that make the data most probable.
Likelihood Function:
Say, we have data, \(D = X_1, X_2, \dots, X_n\) are I.I.D discrete random variable with PMF = \(P_{\Theta}(.)\)
Then, the likelihood function is the probability of observing the data, \(D = \{X_1, X_2, \dots, X_n\}\),
given the parameters \(\Theta\).
Task:
Find the value of parameter \(\Theta_{ML}\) that maximizes the likelihood function.
In order to find the parameter \(\Theta_{ML}\) that maximises the likelihood function,
we need to take the first derivative of the likelihood function with respect to \(\Theta\) and equate it to zero.
But, taking derivative of a product is challenging, so we will take the logarithm on both sides.
Note: Log is a monotonically increasing function, i.e, as x increases, log(x) increases too.
Let us denote the log-likelihood function as \(\bar{L}\).
\[ \begin{aligned} \mathcal{\bar{L}_{X_1, X_2, \dots ,X_n}}(\Theta) &= log [\prod_{i=1}^{n} P_{\Theta}(X_i)] \\ &= \sum_{i=1}^{n} log P_{\Theta}(X_i) \\ \end{aligned} \]Therefore, Maximum Likelihood Estimation is the parameter \(\Theta_{ML}\) that maximises the log-likelihood function.
\[ \Theta_{ML}(X_1, X_2, \dots, X_n) = \underset{\Theta}{\mathrm{argmax}}\ \bar{L}_{X_1, X_2, \dots ,X_n}(\Theta) \]Given \(X_1, X_2, \dots, X_n\) are I.I.D. Bernoulli random variable with PMF as below:
Estimate the parameter \(\theta\) using Maximum Likelihood Estimation.
Let, \(n_1 = \) number of 1’s in the dataset.
Likelihood Function:
Log-Likelihood Function:
Maximum Likelihood Estimation:
In order to find the parameter \(\theta_{ML}\), we need to take the first derivative of the log-likelihood function
with respect to \(\theta\) and equate it to zero.
Read more about Derivative
Say, e.g., we have 10 observations for the Bernoulli random variable as: 1,0,1,1,0,1,1,0,1,0.
Then, the parameter \(\Theta_{ML} = \frac{6}{10} = 0.6\) i.e proportion of 1’s.
Likelihood Function:
Log-Likelihood Function:
Note: Here, the first term \( -\frac{n}{2} log (2\pi) \) is a constant wrt both \(\mu\) and \(\sigma\), so we can ignore the term.
Maximum Likelihood Estimation:
Instead of finding \(\mu\) and \(\sigma\) that maximises the log-likelihood function,
we can find \(\mu\) and \(\sigma\) that minimises the negative of the log-likelihood function.
Now, lets differentiate the log likelihood function wrt \(\mu\) and \(\sigma\) separately to get \(\mu_{ML}, \sigma_{ML}\).
Lets, calculate \(\mu_{ML}\) first by taking the derivative of the log-likelihood function wrt \(\mu\) and equating it to 0.
Read more about Derivative
Similarly, we can calculate \(\sigma_{ML}\) by taking the derivative of the log-likelihood function wrt \(\sigma\)
and equating it to 0.
Note: In general MLE is biased, i.e does NOT give an unbiased estimate => divides by \(n\) instead of \((n-1)\).
Bayesian Statistics:
Bayesian statistics model parameters by updating initial beliefs (prior probabilities) with observed data to form
a final belief (posterior probability) using Bayes’ Theorem.
Instead of a single point estimate, it provides a probability distribution over possible parameter values,
which allows to quantify uncertainty and yields more robust models, especially with limited data.
Bayes’ Theorem:
Read more about Bayes’ Theorem
\(P(\Theta)\): Prior: Initial distribution of \(\Theta\) before seeing the data.
\(P(X \mid \Theta)\): Likelihood: Conditional distribution of data \(X\), given the parameter \(\Theta\).
\(P(\Theta \mid X)\): Posterior: Conditional distribution of parameter \(\Theta\), given the data \(X\).
\(P(X)\): Evidence: Probability of seeing the data \(X\).
Let, \(n_1 = \) number of 1’s in the dataset.
Prior: \(P(\Theta)\) : \(\Theta \sim U(0, 1) \), i.e, parameter \(\Theta\) comes from a continuos uniform
distribution in the range [0,1].
\(f_{\Theta}(\theta) = 1, \theta \in [0, 1] \)
Likelihood: \(P_{X \mid \Theta}(x \mid \theta) = \theta^{n_1} (1 - \theta)^{n - n_1} \).
Posterior:
\[ f_{\Theta \mid X} (\theta \mid x) = \frac{f_{\Theta}(\theta) P_{X \mid \Theta}(x \mid \theta)}{f_{X}(x)} \\ \]Note: The most difficult part is to calculate the denominator \(f_{X}(x)\).
So, either we try NOT to compute it all together, or we try to map it to some known functions to make calculations easier.
We know that we can get the marginal probability by integrating the joint probability over another variable.
Also from conditional probability, we know:
\[ \tag{2} f_{X \mid Y}(x \mid y) = \frac{f_{X,Y}(x,y)}{f_{Y}(y)} \\ => f_{X,Y}(x,y) = f_{Y}(y) f_{X \mid Y}(x \mid y) \]From equations 1 and 2, we have:
\[ \tag{3} f_{X}(x) = \int_{Y}f_{Y}(y) f_{X \mid Y}(x \mid y)dy \]Now let’s replace the value of \(f_{X}(x) \) in the posterior from equation 3:
Posterior:
Beta Function:
It is a special mathematical function denoted by B(a, b) or β(a, b) that is defined by the integral formula:
Note: We can see that the denominator of the posterior is of the form of Beta function.
Posterior:
Suppose, in the above example, we are told that the parameter \(\Theta\) is closer to 1 than 0.
How will we incorporate this useful information (apriori knowledge) into our parameter estimation?
Since, we know apriori that \(\Theta\) is closer to 1 than 0, we should take this initial belief into account
to do our parameter estimation.
Prior:
Posterior:
\[ \begin{aligned} f_{\Theta \mid X} (\theta \mid x) &= \frac{f_{\Theta}(\theta) P_{X \mid \Theta}(x \mid \theta)}{f_{X}(x)} \\[10pt] &= \frac{f_{\Theta}(\theta) P_{X \mid \Theta}(x \mid \theta)}{\int_{\Theta}f_{\Theta}(\theta) P_{X \mid \Theta}(x \mid \theta)d\theta} \\[10pt] &= \frac{f_{\Theta}(\theta) P_{X \mid \Theta}(x \mid \theta)}{\int_{0}^1f_{\Theta}(\theta) P_{X \mid \Theta}(x \mid \theta)d\theta} \\[10pt] \text{ We know that: } f_{\Theta}(\theta) = 2\Theta, \theta \in [0, 1] \\ &= \frac{2\Theta * P_{X \mid \Theta}(x \mid \theta)}{\int_{0}^1 2\Theta* P_{X \mid \Theta}(x \mid \theta)d\theta} \\[10pt] & = \frac{2\Theta * \theta^{n_1} (1 - \theta)^{n - n_1}}{\int_{0}^1 2\Theta * \theta^{n_1} (1 - \theta)^{n - n_1}} \\[10pt] => f_{\Theta \mid X} (\theta \mid x) &= \frac{\theta^{n_1+1} (1 - \theta)^{n - n_1}}{β(n_1+2, n-n_1+1)} \end{aligned} \]Note: If we do NOT have enough data, then we should NOT ignore our intial belief.
However, if we have enough data, then the data will override our initial belief and the posterior will be dominated by data.
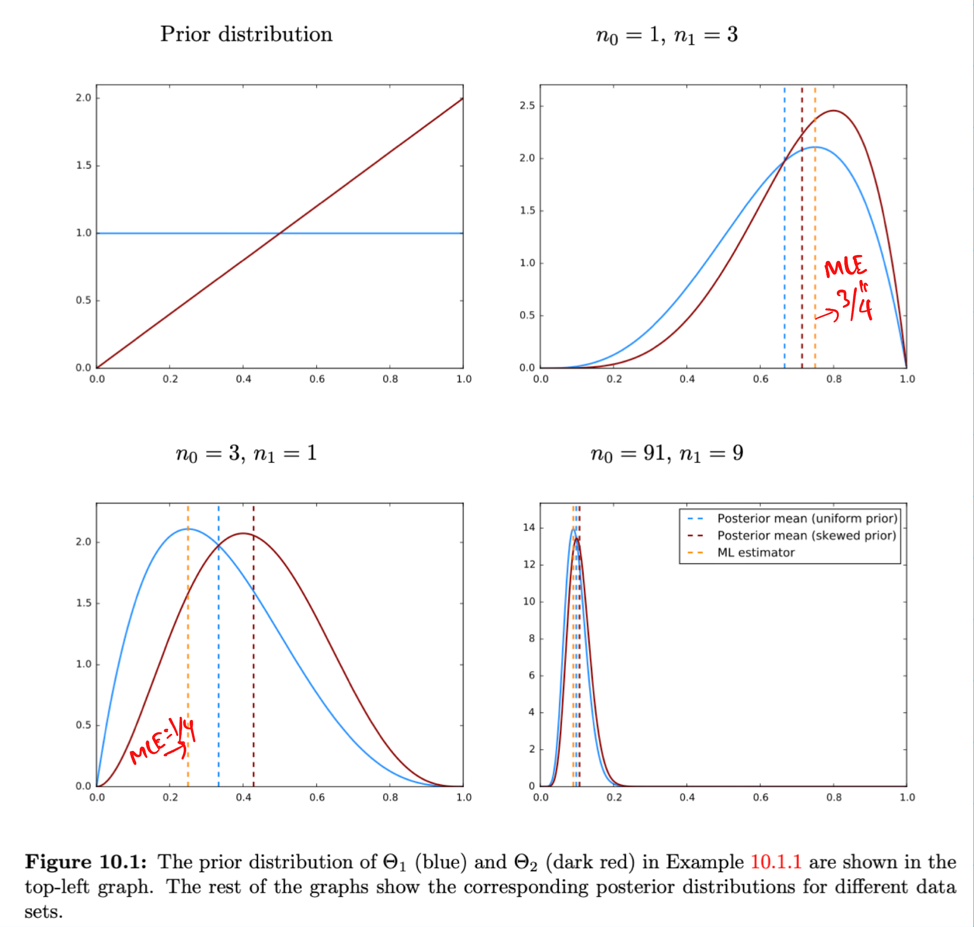
Note: Bayesian approach gives us a probability distribution of parameter \(\Theta\).
We can use Bayesian Point Estimators, after getting the posterior distribution, to summarize it with a single value for
practical use, such as,
Maximum A Posteriori (MAP) Estimator:
It finds the mode(peak) of the posterior distribution.
Given that :
\(\Theta\) is discrete, with probability 0.5 for both 0 and 1.
=> The Gaussian distribution is equally likely to be centered at 0 or 1.
Variance: \(\sigma^2 = 1\)
Prior:
Likelihood:
Posterior:
We need to find:
\[ \underset{\Theta}{\mathrm{argmax}}\ P_{\Theta \mid X} (\theta \mid x) \]Taking log on both sides:
Let’s calculate the log-likelihood function first -
\[ \begin{aligned} \log f_{X \mid \Theta}(x \mid \theta) &= \log \prod_{i=1}^n \frac{1}{\sqrt{2\pi}} e^{-\frac{(x_i-\theta)^2}{2}} \\ &= log(\frac{1}{\sqrt{2\pi}})^n + \sum_{i=1}^n \log (e^{-\frac{(x_i-\theta)^2}{2}}), \text{ since \(\sigma = 1\)} \\ &= n\log(\frac{1}{\sqrt{2\pi}}) + \sum_{i=1}^n -\frac{(x_i-\theta)^2}{2} \\ => \tag{2} \log f_{X \mid \Theta}(x \mid \theta) &= n\log(\frac{1}{\sqrt{2\pi}}) - \sum_{i=1}^n \frac{(x_i-\theta)^2}{2} \end{aligned} \]Here computing \(f_{X}(x)\) is difficult.
So, instead of differentiating above equation wrt \(\Theta\), and equating to 0,
we will calculate the above expression for \(\theta=0\) and \(\theta=1\) and compare the values.
This way we can get rid of the common value \(f_{X}(x)\) in both expressions that is not dependent on \(\Theta\).
When \(\theta=1\):
Similarly, when \(\theta=0\):
So, we can say that \(\theta = 1\) only if :
the value of the above expression for \(\theta = 1\) > the value of the above expression for \(\theta = 0\)
From equation 3 and 4:
Note: If the prior is uniform then \(\Theta_{MAP} = \Theta_{MLE}\), because uniform prior does NOT give any information about the initial bias, and all possibilities are equally likely.
What if, in the above example, we know that the initial belief is not uniform but biased towards 0?
Prior:
Now, let’s compare the log-posterior for both the cases i.e \(\theta=0\) and \(\theta=1\) as we did earlier.
But, note that this time the probabilities for \(\theta=0\) and \(\theta=1\) are different.
So, we can say that \(\theta = 1\) only if :
the value of the above expression for \(\theta = 1\) > the value of the above expression for \(\theta = 0\)
From equation 3 and 4 above:
Therefore, we can see that \(\Theta_{MAP}\) is extra biased towards 0.
Note: For a non-uniform prior \(\Theta_{MAP}\) estimate will be pulled towards the prior’s mode.
Minimum Mean Square Error (MMSE) Estimation:
Minimizes the expected value of squared error.
Mean of the posterior distribution is the conditional expectation of parameter \(\Theta\), given the data.
\(\hat\Theta(X)\): Predicted value.
\(\Theta\): Actual value.
Let’s revisit the above examples that we used for MLE.
Case 1: Uniform Continuous Prior for parameter \(\Theta\) of Bernoulli distribution
Prior:
Posterior:
Let’s calculate the \(\Theta_{MMSE}\):
Similarly, for the second case where the prior is biased towards 1.
Case 2: Prior is biased towards 1 for parameter \(\Theta\) of Bernoulli distribution
Prior:
Posterior:
So, here in this case our \(\Theta_{MMSE}\) is:
End of Section
This sheet contains all the topics that will be covered for Statistics for AI & ML.
Measures of Central Tendency:
A single number that describes the central, typical, or representative value of a dataset, e.g, mean, median, and mode.
The mean is the average, the median is the middle value in a sorted list, and the mode is the most frequently occurring value.
Mean:
The artihmetic average of a set of numbers i.e sum all values and divide by the number of values.
\(mean = \frac{1}{n}\sum_{i=1}^{n}x_i\)
Pros:
Cons:
For example:
Median:
The middle value of a sorted list of numbers. It divides the dataset into 2 equal halves.
Calculation:
Pros:
Cons:
For example:
Mode:
The most frequently occurring value in a dataset.
Pros:
Cons:
Range:
The difference between the largest and smallest values in a dataset. Simplest measure of dispersion
\(range = max - min\)
Pros:
Cons:
Variance:
The average of the squared distance of each value from the mean.
Measures the spread of data points.
\(sample ~ variance = s^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2\)
\(population ~ variance = \sigma^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \mu)^2\)
Cons:
Standard Deviation:
The square root of the variance, measures average distance of data points from the mean.
\(s = sample ~ standard ~ deviation \)
\(\sigma = population ~ standard ~ deviation \)
For example:
Mean Absolute Deviation:
It is the average of absolute deviation or distance of all data points from mean.
\( mad = \frac{1}{n}\sum_{i=1}^{n}|x_i - \bar{x}| \)
Pros:
For example:
Skewness:
It measures the asymmetry of a data distribution.
Tells us whether the data is concentrated on one side of mean and is there a long tail stretching on the other side.
Positive Skew:
Negative Skew:
Zero Skew:
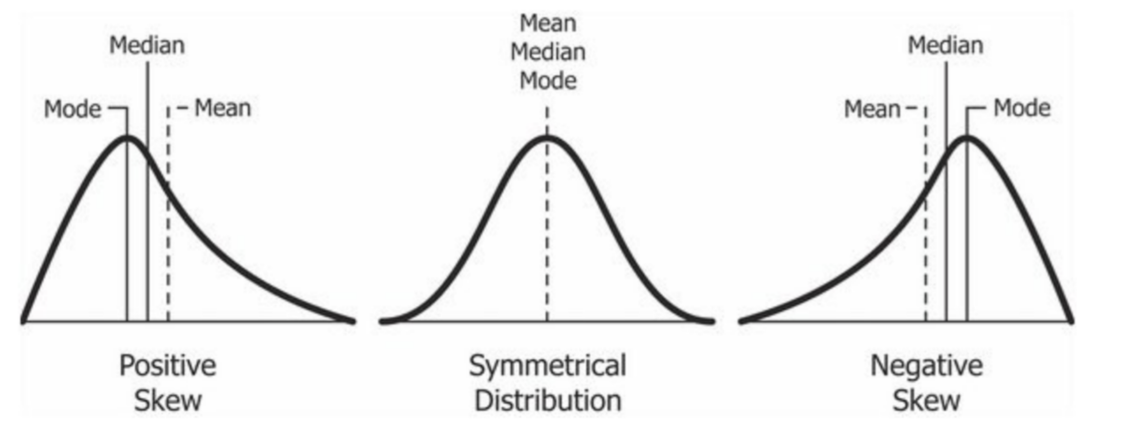
For example:
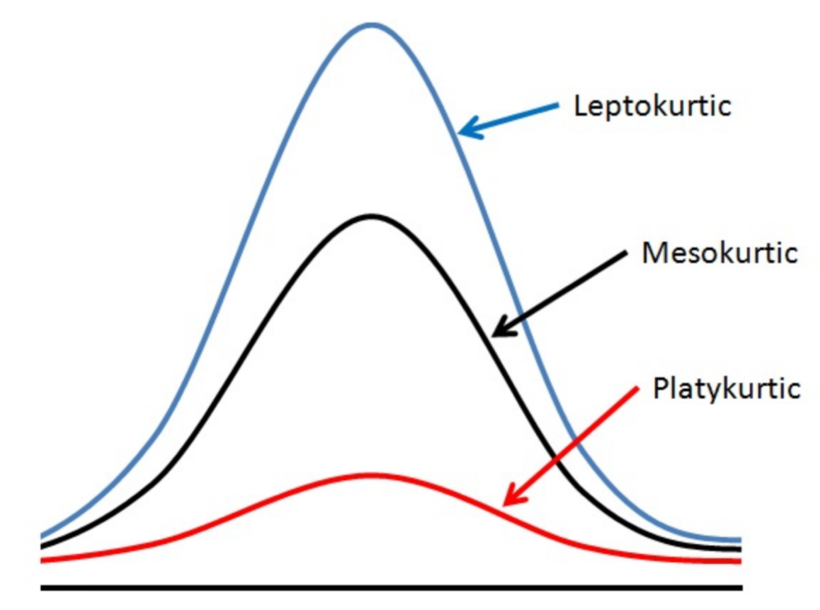
Kurtosis:
It measures the “tailedness” of a data distribution.
It describes how much the data is concentrated in tails (fat or thin) versus the center.
Excess Kurtosis:
Excess kurtosis is calculated by subtracting 3 from standard kurtosis in order to compare with normal distribution.
Normal distribution has kurtosis = 3.
Mesokurtic:
Leptokurtic:
Platykurtic:
Percentile:
It indicates the percentage of scores in a dataset that are equal to or below a specific value.
Here, the complete dataset is divided into 100 equal parts.
Quartile:
They are special percentiles that divide the complete dataset into 4 equal parts.
Q1 => 25th percentile, value below which 25% of the data falls.
Q2 => 50th percentile, value below which 50% of the data falls; median.
Q3 => 75th percentile, value below which 75% of the data falls.
For example:
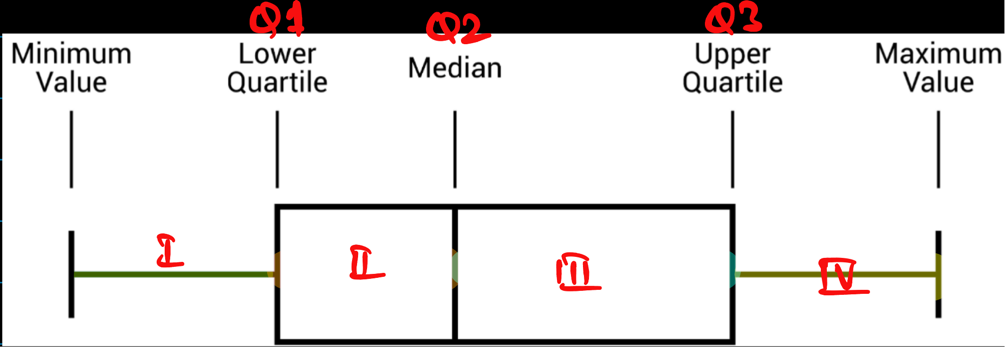
Inter Quartile Range(IQR):
It is the single number that measures the spread of middle 50% of the data, i.e Q1-Q3.
IQR = Q3 - Q1
For example:
Therefore, IQR = Q3-Q1 = 9-3 = 6
IQR is a standard tool for detecting outliers.
Values that fall outside the ‘fences’ can be considered as potential outliers.
Lower fence = Q1 - 1.5 * IQR
Upper fence = Q3 + 1.5 * IQR
IQR = Q3-Q1 = 9-3 = 6
Lower fence = Q1 - 1.5 * IQR = 3 - 9 = -6
Upper fence = Q3 + 1.5 * IQR = 9 + 9 = 18
So, any data point that is less than -6 or greater than 18 is considered as a potential outlier.
As in this example, 100 can be considered as an outlier.
Even though the above metrics give us a good idea of the data distribution,
but still we should always plot the data and visually inspect the data distribution.
As these metrics may not provide the complete picture.
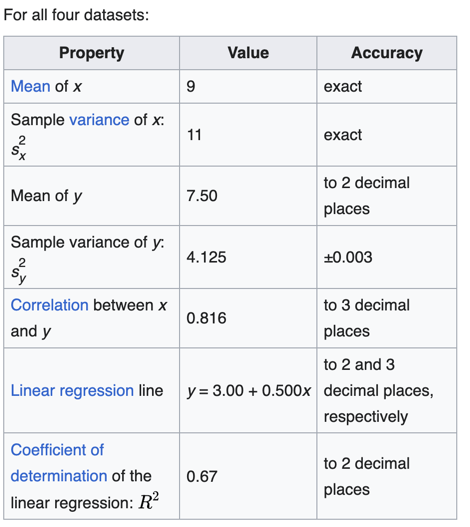
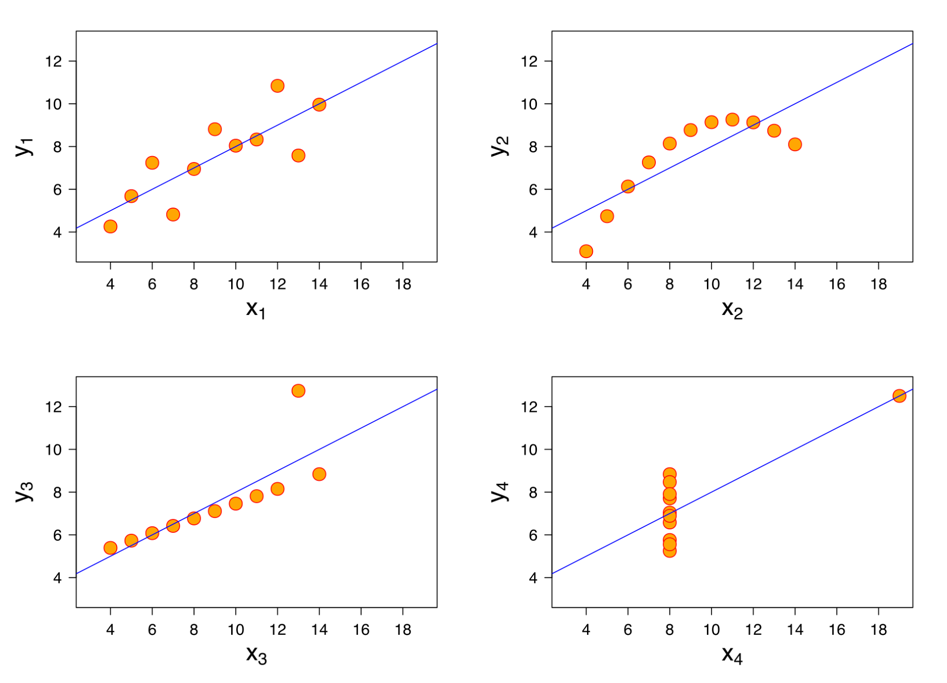
A mathematician called Francis John Anscombe has illustrated this point beautifully in his Anscombe’s Quartet.
Anscombe’s quartet:
It comprises four datasets that have nearly identical simple descriptive statistics,
yet have very different distributions and appear very different when plotted.
End of Section
Covariance:
It measures the direction of linear relationship between two variables \(X\) and \(Y\).
\(N\) = size of population
\(\mu_{x}\) = population mean of \(X\)
\(\mu_{y}\) = population mean of \(Y\)
\(n\) = size of sample
\(\bar{x}\) = sample mean of \(X\)
\(\bar{y}\) = sample mean of \(Y\)
Note: We have a term (n-1) instead of n in the denominator to make it an unbiased estimate, called Bessel’s Correction.
If both \((x_i - \bar{x})\) and \((y_i - \bar{y})\) have the same sign, then the product is positive(+ve).
If both \((x_i - \bar{x})\) and \((y_i - \bar{y})\) have opposite signs, then the product is negative(-ve).
The final value of covariance depends on the sum of the above individual products.
\( \begin{aligned} \text{Cov}(X, Y) &> 0 &&\Rightarrow \text{ } X \text{ and } Y \text{ increase or decrease together} \\ \text{Cov}(X, Y) &= 0 &&\Rightarrow \text{ } \text{No linear relationship} \\ \text{Cov}(X, Y) &< 0 &&\Rightarrow \text{ } \text{If } X \text{ increases, } Y \text{ decreases (and vice versa)} \end{aligned} \)
Limitation:
Covariance is scale-dependent, i.e, units of X and Y impact its magnitude.
This makes it hard to make comparisons of covariance across different datasets.
E.g: Covariance between age and height will NOT be same as the covariance between years of experience and salary.
Note:It only measures the direction of the relationship, but does NOT give any information about the strength of the relationship.
Correlation:
It measures both the strength and direction of the linear relationship between two variables \(X\) and \(Y\).
It is a standardized version of covariance that gives a dimensionless measure of linear relationship.
There are 2 popular ways to calculate correlation coefficient:
Pearson Correlation Coefficient (r):
It is a standardized version of covariance and most widely used measure of correlation.
Assumption: Data is normally distributed.
\(\sigma_{x}\) and \(\sigma_{y}\) are the standard deviations of \(X\) and \(Y\).
Range of \(r\) is between -1 and 1.
\(r = 1\) => perfect +ve linear relationship between X and Y
\(r = -1\) => perfect -ve linear relationship between X and Y
\(r = 0\) => NO linear relationship between X and Y.
Note: A correlation coefficient of 0.9 means that there is a strong linear relationship between X and Y,
irrespective of their units.
Let’s calculate the standard deviation of \(X\) and \(Y\):
\(\sigma_{x} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2} \)
\(= \sqrt{\frac{1}{3-1}[(1-2)^2 + (2-2)^2 + (3-2)^2]}\)
\(= \sqrt{\frac{1+0+1}{2}} =\sqrt{\frac{2}{2}} = 1 \)
Similarly, we can calculate the standard deviation of \(Y\):
\(\sigma_{y} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(y_i - \bar{y})^2} \)
\(= \sqrt{\frac{1}{3-1}[(2-4)^2 + (4-4)^2 + (6-4)^2]}\)
\(= \sqrt{\frac{4+0+4}{2}} =\sqrt{\frac{8}{2}} = 2 \)
Now, we can calulate the pearson correlation coefficient (r):
\(r_{xy} = \frac{Cov(X, Y)}{\sigma_{x} \sigma_{y}}\)
=> \(r_{xy} = \frac{2}{1* 2}\)
=> \(r_{xy} = 1\)
Therefore, we can say that there is a strong +ve linear relationship between X and Y.
Spearman Rank Correlation Coefficient (\(\rho\)):
It is a measure of the strength and direction of the monotonic relationship between two ranked variables \(X\) and \(Y\).
It captures monotonic relationship, meaning the variables move in the same or opposite direction,
but not necessarily a linear relationship.
| Student | Teacher A Rank | Teacher B Rank | \(d_i\) | \(d_i^2\) |
|---|---|---|---|---|
| S1 | 1 | 2 | -1 | 1 |
| S2 | 2 | 1 | 1 | 1 |
| S3 | 3 | 3 | 0 | 0 |
| S4 | 4 | 5 | -1 | 1 |
| S5 | 5 | 4 | 1 | 1 |
\(\sum_{i}d_i^2 = 4 \)
\( n = 5 \)
\(\rho_{xy} = 1 - \frac{6\sum_{i}d_i^2}{n(n^2-1)}\)
=> \(\rho_{xy} = 1 - \frac{6*4}{5(5^2-1)}\)
=> \(\rho_{xy} = 1 - \frac{24}{5*24}\)
=> \(\rho_{xy} = 1 - \frac{1}{5}\)
=> \(\rho_{xy} = 0.8\)
Therefore, we can say that there is a strong +ve correlation between the ranks given by teacher A and teacher B.
Correlation is very useful in feature selection for training machine learning models.
Causation means that one variable directly causes the change in another variable, i.e, direct
cause->effect relationship.
Whereas, correlation means that two variables move together.
E.g: Election results and stock market - there may be some correlation between the two,
but establishing clear causal links is difficult.
End of Section
Population Mean:
It is the true average of the entire group.
It describe the central tendency of the entire population.
\( \mu = \frac{1}{N}\sum_{i=1}^{N}x_i \)
N: Number of data points
Sample Mean:
It is the average of a smaller representative subset (a sample) of the entire population.
It provides an estimate of the population mean.
\( \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i \)
n: size of sample
Central Limit Theorem:
This law states that for a sequence of of I.I.D random variables \( X_1, X_2, \dots, X_n \),
with finite mean and variance, the distribution of the sample mean \( \bar{X} \) approaches a normal distribution
as \( n \rightarrow \infty \), regardless of its original population distribution.
The distribution of the sample mean is : \( \bar{X} \sim N(\mu, \sigma^2/n)\)
Let, \( X_1, X_2, \dots, X_n \) are I.I.D random variables.
Now, let’s calculate the variance of sample means.
We know that:
Let’s apply above 2 rules on the variance of sample means equation above:
\[ \begin{aligned} Var[\bar{X_n}] &= Var[\frac{1}{n}(X_1+ X_2+ \dots+ X_n)] \\ &= \frac{1}{n^2}[Var[X_1+ X_2+ \dots+ X_n]] \\ &= \frac{1}{n^2}[Var[X_1] + Var[X_2] + \dots + Var[X_n]] \\ \text{We know that: } Var[X_i] = \sigma^2 \\ &= \frac{1}{n^2}[\sigma^2 + \sigma^2 + \dots + \sigma^2] \\ &= \frac{n\sigma^2}{n^2} \\ => Var[\bar{X_n}] &= \frac{\sigma^2}{n} \end{aligned} \]Since, standard deviation = \(\sigma = \sqrt{Variance}\)
Therefore, Standard Deviation\([\bar{X_n}] = \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}\)
The standard deviation of the sample means is also known as “Standard Error”.
Note: We can also standardize the sample mean, i.e, mean centering and variance scaling.
Standardisation helps us to use the Z-tables of normal distribution.
We know that, a standardized random variable \(Y_i = \frac{X_i - \mu}{\sigma}\)
Similarly, standardized sample mean:
Note: For practical purposes, \(n \ge 30\) is considered as a sufficient sample size for the CLT to hold.
Note:
The variance must be finite, else, the sample mean will NOT converge to a normal distribution.
If a distribution has a heavy tail, then the expected value calculation diverges.
e.g:
End of Section
Confidence Interval:
It is a range of values that is likely to contain the true population mean, based on a sample.
Instead of giving a point estimate, it gives a range of values with confidence level.
For normal distribution, confidence interval :
\(\bar{X}\): Sample mean
\(Z\): Z-score corresponding to confidence level
\(n\): Sample size
\( \sigma \): Population Standard Deviation
Applications:
95% confidence interval does NOT mean there is a 95% chance that the true mean lies in the specific calculated interval.
For example:
Let’s suppose we want to measure the average weight of a certain species of dog.
We want to estimate the true population
mean \(\mu\) using confidence interval.
Note: True average weight = 30 kg, but this is NOT known to us.
| Sample Number | Sample Mean | 95% Confidence Interval | Did it capture \(\mu\) ? |
|---|---|---|---|
| 1 | 29.8 kg | (28.5, 31.1) | Yes |
| 2 | 30.4 kg | (29.1, 31.7) | Yes |
| 3 | 31.5 kg | (30.2, 32.8) | No |
| 4 | 28.1 kg | (26.7, 29.3) | No |
| - | - | - | - |
| - | - | - | - |
| - | - | - | - |
| 100 | 29.9 kg | (28.6, 31.2) | Yes |
Suggest which company is offering a better salary?
Below is the details of the salaries based on a survey of 50 employees.
| Company | Average Salary(INR) | Standard Deviation |
|---|---|---|
| A | 36 lpa | 7 lpa |
| B | 40 lpa | 14 lpa |
For comparison, let’s calculate the 95% confidence interval for the average salaries of both companies A and B.
We know that:
\( CI = \bar{X} \pm Z\frac{\sigma}{\sqrt{n}} \)
Margin of Error(MoE) \( = Z\frac{\sigma}{\sqrt{n}} \)
Z-Score for 95% CI = 1.96
\(MoE_A = 1.96*\frac{7}{\sqrt{50}} \approx 1.94 \)
=> 95% CI for A = \(36 \pm 1.94 \) = [34.06, 37.94]
\(MoE_B = 1.96*\frac{14}{\sqrt{50}} \approx 3.88\)
=> 95% CI for B = \(40 \pm 3.88 \) = [36.12, 43.88]
We can see that initially company B’s salary looked obviously better,
but after calculating the 95% CI, we can see that there is a significant overlap in the salaries of two companies,
i.e [36.12, 37.94].
End of Section
Hypothesis Testing is used to determine whether a claim or theory about a population is supported by a sample data,
by assessing whether observed difference or patterns are likely due to chance or represent a true effect.
Hypothesis Testing:
It is a statistical inference framework used to make decisions about a population parameter, such as, the mean, variance,
distribution, correlation, etc., based on a sample of data.
It provides a formal method to evaluate competing claims.
Null Hypothesis (\(H_0\)):
Status quo or no-effect or no difference statement; almost always contains a statement of equality.
Alternative Hypothesis (\(H_1 ~or~ H_a\)):
The statement representing an effect, a difference, or a relationship.
It must be true if the null hypothesis is rejected.
Say, the data, D: <patient_id, med_1/med_2, recovery_time(in days)>
We need some metric to compare the recovery times of 2 medicines.
We can use the mean recovery time as the metric, because we know that we can use following techniques for comparison:
Note: Let’s assume the sample size \(n < 30\), because medical tests usually have small sample sizes.
=> We will use the 2-Sample T-Test; we will continue using T-Test throughout the discussion.
Step 1: Define the null and alternative hypotheses.
Null Hypothesis \(H_0\): The mean recovery time of 2 medicines is the same i.e \(Mean_{m1} = Mean_{m2}\) or \(m_{m1} = m_{m2}\).
Alternate Hypothesis \(H_a\): \(m_{m1} < m_{m2}\) (1-Sided T-Test) or \(m_{m1} ⍯ m_{m2}\) (2-Sided T-Test).
Step 2: Select a relevant statistical test for the task with associated test statistic.
Let’s do a 2 sample T-Test, i.e, \(m_{m1} < m_{m2}\)
Step 3: Calculate the test statistic under null hypothesis.
Test Statistic:
For 2 sample T-Test:
s: Standard Deviation
n: Sample Size
Note: If the 2 means are very close then \(t_{obs} \approx 0\).
Step 4: Suppose significance level (\(\alpha\)) = 5% or 0.05.
Step 5: Compute the p-value from the observed value of test-statistic.
P-Value:
p-value = area under curve = probability of observing test statistic \( \ge t_{obs} \) if the null hypothesis is true.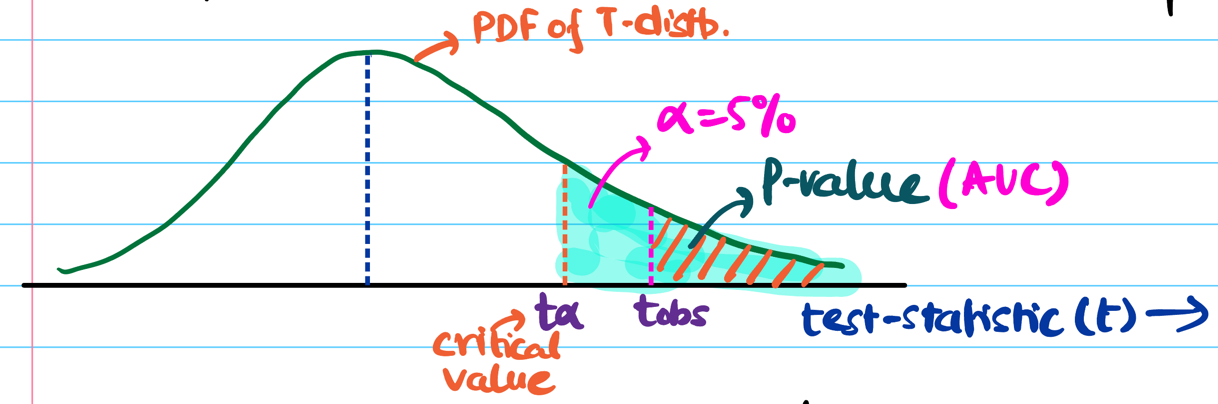
Step 6: Accept or reject the null hypothesis, based on the significance level (\(\alpha\)).
If \(p_{value} < \alpha\), we reject the null hypothesis and accept the alternative hypothesis and vice versa.
Note: In the above example \(p_{value} < \alpha\), so we reject the null hypothesis.
We need to do a left or right sided test, or a 2-sided test, this depends upon our alternate hypothesis and test statistic.
Let’s continue our 2 sample mean T-test to understand the concept:
Left Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 < medicine 2, i.e, \(m_{m_1} < m_{m_2}\)
=> \(m_{m_1} - m_{m_2} < 0\)
Since, the denominator in above equation is always positive.
=> \(t_{obs} < 0\)
Therefore, we need to do a left sided/tailed test.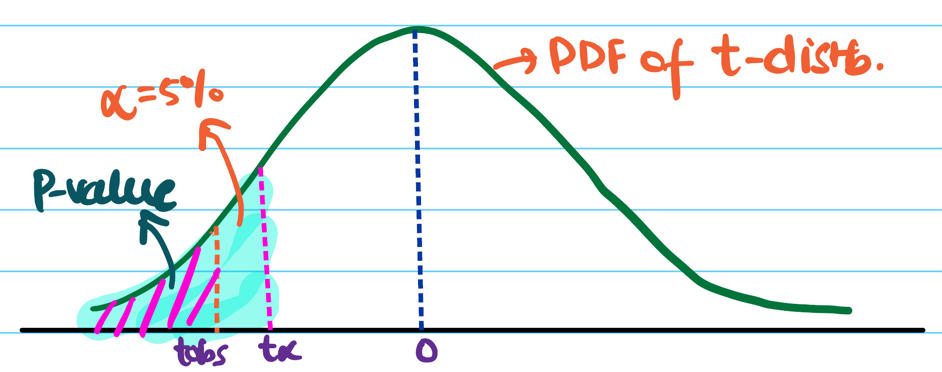
So, we want \(t_{obs}\) to be very negative to confidently conclude that alternate hypothesis is true.
Right Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 > medicine 2, i.e, \(m_{m_1} > m_{m_2}\)
=> \(m_{m_1} - m_{m_2} > 0\)
Similarly, here we need to do a right sided/tailed test.
2 Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 ⍯ medicine 2, i.e, \(m_{m_1} ⍯ ~ m_{m_2}\)
=> \(m_{m_1} - m_{m_2} < 0\) or \(m_{m_1} - m_{m_2} > 0\)
If \(H_a\) is true then \(t_{obs}\) is a large -ve value or a large +ve value.
Since, t-distribution is symmetric, we can divide the significance level \(\alpha\) into 2 equal parts.
i.e \(\alpha = 2.5\%\) on each side.
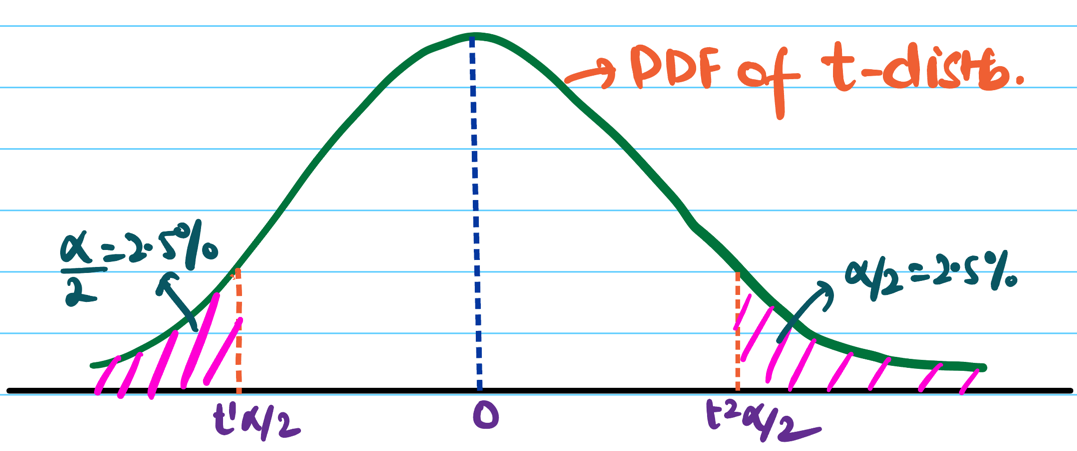
So, we want \(t_{obs}\) to be very negative or very positive to confidently conclude that the alternate hypothesis is true.
We accept \(H_a\) if \(t_{obs} < t^1_{\alpha/2}\) or \(t_{obs} > t^2_{\alpha/2}\).
Note: For critical applications ‘\(\alpha\)’ can be very small i.e. 0.1% or 0.01%, e.g medicine.
Significance Level (\(\alpha\)):
It is the probability of wrongly rejecting a true null hypothesis, known as a Type I error or false +ve rate.
Critical Value:
It is a specific point on the test-statistic distribution that defines the boundaries of the null hypothesis
acceptance/rejection region.
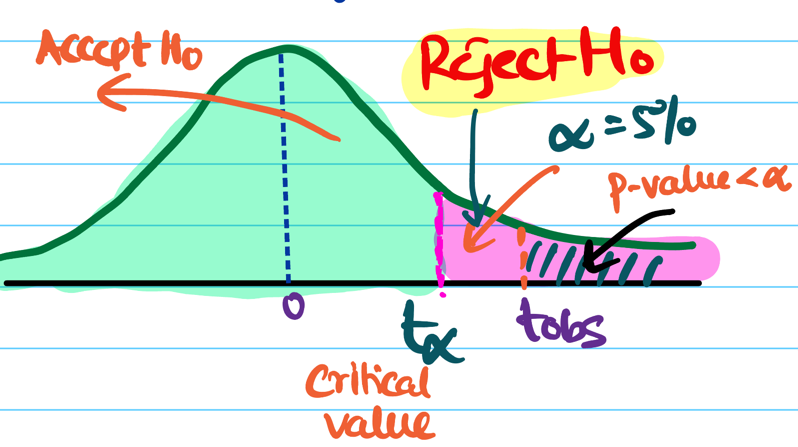
Power of Test:
It is the probability that a hypothesis test will correctly reject a false null hypothesis (\(H_{0}\))
when the alternative hypothesis (\(H_{a}\)) is true.

Yes, having a large sample size makes a hypothesis test more powerful.
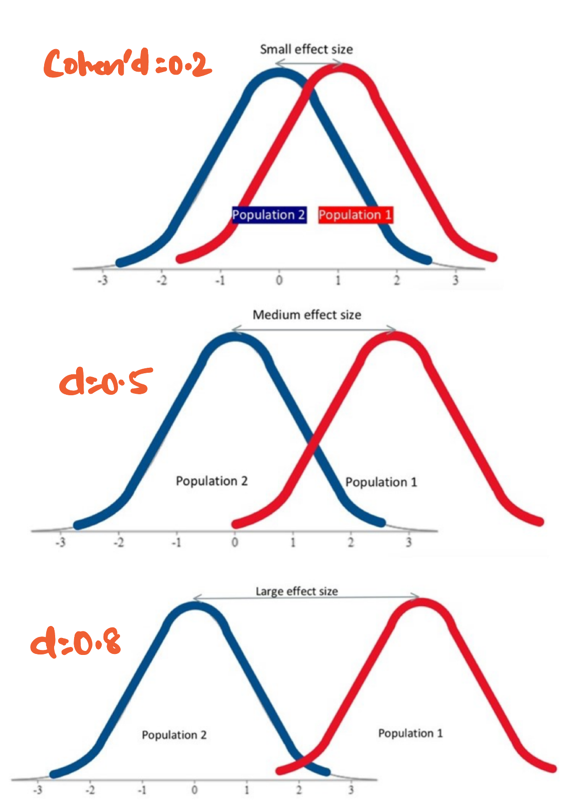
Effect Size:
It is a standardized objective measure that complements p-value by clarifying whether a statistically significant
finding has any real world relevance.
It quantifies the magnitude of relationship between two variables.
Effect size is measured using Cohen’s d formula:
\(\bar{X}\): Sample mean
\(s_p\): Pooled Standard deviation
\(n\): Sample size
\(s\): Standard deviation
Note: Theoretically, Cohen’s d value can range from negative infinity to positive infinity.
but for practical purposes, we use the following value:
small effect (\(d=0.2\)), medium effect (\(d=0.5\)), and large effect (\(d\ge 0.8\)).
End of Section
T-Test:
It is a statistical test that is used to determine whether the sample mean is equal to a hypothesized value or
is there a significant difference between the sample means of 2 groups.
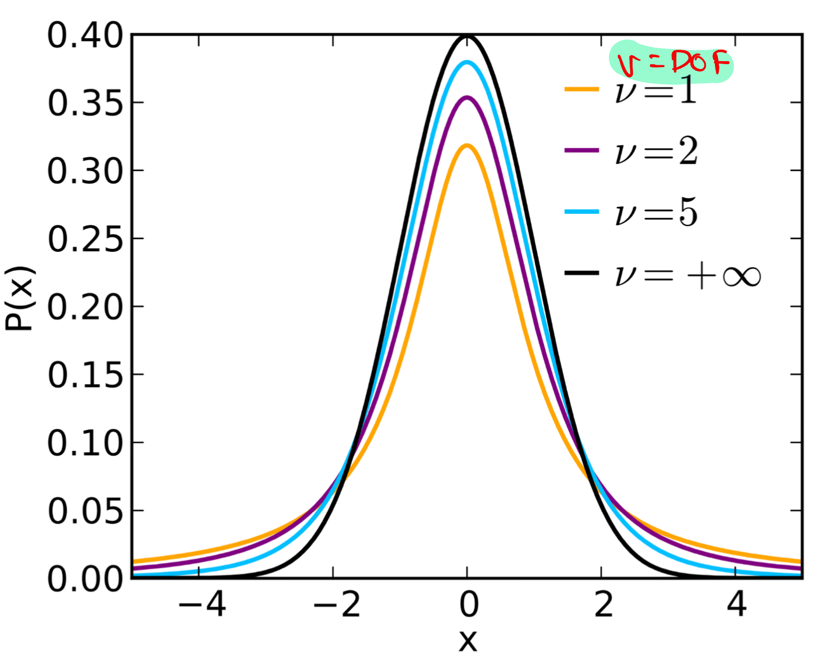
Student’s t-distribution:
It is a continuous probability distribution that is a symmetrical, bell-shaped curve similar
to the normal distribution but with heavier tails.
There are 3 types of T-Test:
1-Sample T-Test:
It is used to test whether the sample mean is equal to a known/hypothesized value.
Test statistic (t):
where,
\(\bar{x}\): sample mean
\(\mu\): hypothesized value
\(s\): sample standard deviation
\(n\): sample size
\(\nu = n-1 \): degrees of freedom
Let’s verify developer’s claim using the tester’s test results using 1 sample t-test.
Null hypothesis: \(H_0\) = The average API response time is 100 ms, i.e, \(\bar{x} = \mu\).
Alternative hypothesis: \(H_a\) = The average API response time > 100 ms, i.e, \(\bar{x} > \mu\) => right tailed test.
Hypothesized mean \(\mu\) = 100 ms
Sample mean \(\bar{x}\) = 115 ms
Sample standard deviation \(s\) = 25 ms
Sample size \(n\) = 20
Degrees of freedom \(\nu\) = 19
\( t_{obs} = \frac{\bar{x} - \mu}{s/\sqrt{n}}\) = \(\frac{115 - 100}{25/\sqrt{20}}\)
= \(\frac{15\sqrt{20}}{25} = \frac{3\sqrt{20}}{5} \approx 2.68\)
Let significance level \(\alpha\) = 5% =0.05.
Critical value \(t_{0.05}\) = 1.729
Important: Find the value of \(t_{\alpha}\) in T-table
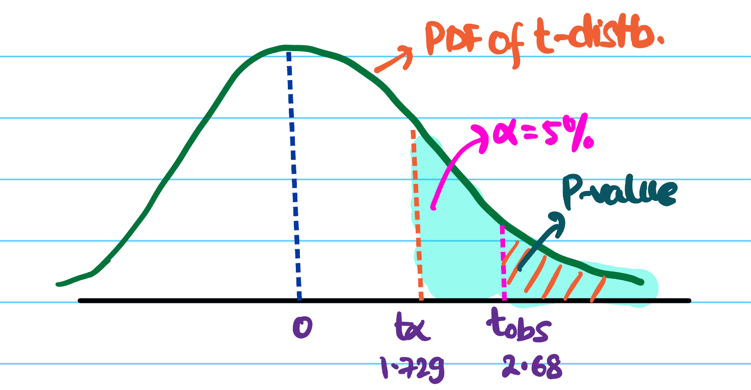
Since \(t_{obs}\) > \(t_{0.05}\), we reject the null hypothesis.
And, accept the alternative hypothesis that the API response time is significantly > 100 ms.
Hence, the developer’s claim is NOT valid.
2-Sample T-Test:
It is used to determine whether there is a significant difference between the means of two independent groups.
There are 2 types of 2-sample t-test:
Unequal Variance:
In this case, the variance of 2 independent groups is not equal.
Also called, Welch’s t-test.
Test statistic (t):
Equal Variance:
In this case, both samples come from equal or approximately equal variance.
Test statistic (t):
Here, degrees of freedom (for equal variance) \(\nu\) = \(n_1 + n_2 - 2\).
\(\bar{x}\): sample mean
\(s\): sample standard deviation
\(n\): sample size
\(\nu\): degrees of freedom
The AI team wants to validate whether the new ML model accuracy is better than the existing model’s accuracy.
Below is the data for the existing model and the new model.
| New Model (A) | Existing Model (B) | |
|---|---|---|
| Sample size (n) | 24 | 18 |
| Sample mean (\(\bar{x}\)) | 91% | 88% |
| Sample std. dev. (s) | 4% | 3% |
Given that the variance of accuracy scores of new and existing models are almost same.
Now, let’s follow our hypothesis testing framework.
Null hypothesis: \(H_0\): The accuracy of new model is same as the accuracy of existing model.
Alternative hypothesis: \(H_a\): The new model’s accuracy is better/greater than the existing model’s accuracy => right tailed test
Let’s solve this using 2 sample T-Test, since the sample size n < 30.
Since the variance of 2 sample are almost equal then we can use the pooled variance method.
Next let’s compute the test statistic, under null hypothesis.
DOF \(\nu\) = \(24+18-2\) = 42 - 2 = 40
Let significance level \(\alpha\) = 5% =0.05.
Critical value \(t_{0.05}\) = 1.684
Important: Find the value of \(t_{\alpha}\) in T-table
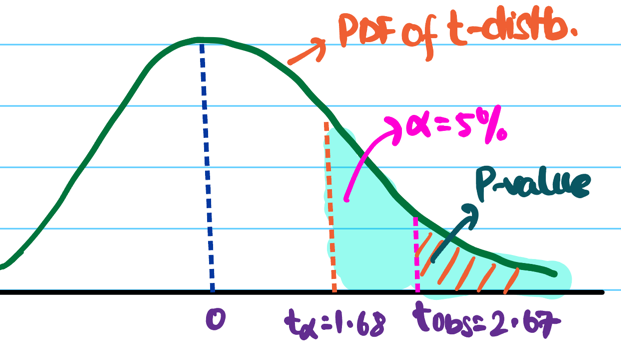
Since \(t_{obs}\) > \(t_{0.05}\), we reject the null hypothesis.
And, accept the alternative hypothesis that the new model has better accuracy than the existing model.
End of Section
Z-Test:
It is a statistical test used to determine whether there is a significant difference between mean of 2 groups or sample and population mean.
There are 2 types of Z-Test:
Z-Score:
It is a standardized score that measures how many standard deviations a particular data point is away from the population mean \(\mu\).
Z-score is calculated as:
\[Z = \frac{x - \mu}{\sigma}\]x: data point
\(\mu\): population mean
\(\sigma\): population standard deviation
e.g:
Z-score helps to define probability areas:
Note:
1-Sample Z-Test:
It is used to test whether the sample mean \(\bar{x}\) is significantly different from a known population mean \(\mu\).
Test Statistic:
\(\bar{x}\): sample mean
\(\mu\): hypothesized population mean
\(\sigma\): population standard deviation
\(n\): sample size
\(\sigma / \sqrt{n}\): standard error of mean
Read more about Standard Error
Note: Test statistic Z follows a standard normal distribution \(Z \sim \mathcal{N}(0, 1)\).
2-Sample Z-Test:
It is used to test whether the sample means \(\bar{x_1}\) and \(\bar{x_2}\) of 2 independent samples are significantly different from each other.
Test Statistic:
\(\bar{x_1}\): sample mean of first sample
\(\bar{x_2}\): sample mean of second sample
\(\sigma_1\): population standard deviation of first sample
\(\sigma_2\): population standard deviation of second sample
\(n_1\): sample size of first sample
\(n_2\): sample size of second sample
Note: Test statistic Z follows a standard normal distribution \(Z \sim \mathcal{N}(0, 1)\).
Null Hypothesis: \(\mu = 120\) seconds, i.e, no change.
Alternative Hypothesis: \(\mu < 120\) seconds => left tailed test.
We will use 1-sample Z-Test to test the hypothesis.
Test Statistic:
Since, significance level \(\alpha\) = 5% =0.05.
Critical value \(Z_{0.05}\) = -1.645
Important: Find the value of \(Z_{\alpha}\) in Z-Score Table
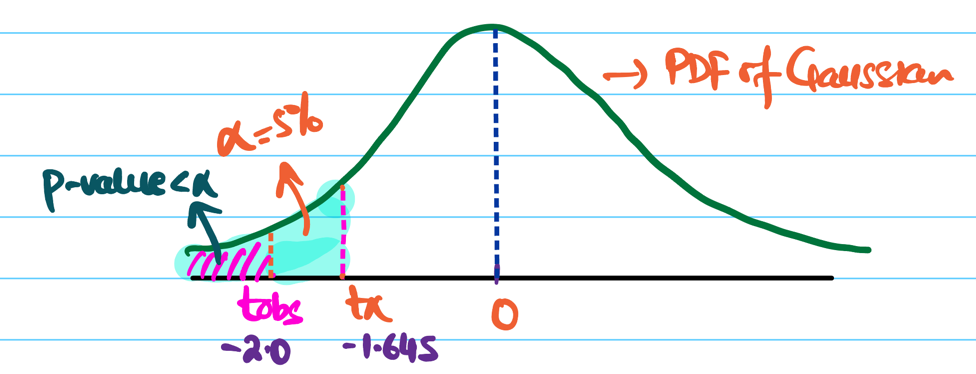
Our \(t_{obs}\) is much more extreme than the the critical value \(Z_{0.05}\), => p-value < 5%.
Hence, we reject the null hypothesis.
Therefore, there is a statistically significant evidence that the new optimisation reduces the runtime of the model.
Z Test of Proportion:
It is a statistical hypothesis test used to determine if there is a significant difference between the proportion
of a characteristic in two independent samples or to compare a sample proportion to a known population value
It is of 2 types:
The categorical data,i.e success/failure, is discrete that can be modeled as Bernoulli distribution.
Let’s understand how this Bernoulli random variable can be approximated as a Gaussian distribution for a very large sample size,
using Central Limit Theorem.
Read more about Central Limit Theorem
Note:We will not prove the complete thing, but we will understand the concept in enough depth for clarity.
\(Y \sim Bernoulli(p)\)
\(X \sim Binomial(n,p)\)
E[X] = mean = np
Var[X] = variance = np(1-p)
X = total number of successes
p = true probability of success
n = number of trials
Proportion of Success in sample = Sample Proportion = \(\hat{p} = \frac{X}{n}\)
e.g.: If n=100 people were surveyed, and 40 said yes, then \(\hat{p} = \frac{40}{100} = 0.4\)
By Central Limit Theorem, we can state that for very large ’n’ Binomial distribution’s mean and variance can be used as an
approximation for Gaussian/Normal distribution:
Since, \(\hat{p} = \frac{X}{n}\)
We can say that:
Mean = \(\mu_{\hat{p}} = p\) = True proportion of success in the entire population
Standard Error = \(SE_{\hat{p}} = \sqrt{Var[\frac{X}{n}]} = \sqrt{\frac{p(1-p)}{n}}\) = Standard Deviation of the sample proportion
Note: Large Sample Condition - Approximation is only valid when the expected number of successes and failures are both > 10 (sometimes 5).
\(np \ge 10 ~and~ n(1-p) \ge 10\)
1-Sample Z-Test of Proportion:
It is used to test whether the observed proportion in a sample differs from hypothesized proportion.
\(\hat{p} = \frac{X}{n}\): Proportion of success observed in a sample
\(p_0\): Specific propotion value under the null hypothesis
\(SE_0\): Standard error of sample proportion under the null hypothesis
Z-Statistic: Measures how many standard errors is the observed sample proportion \(\hat{p}\) away from \(p_0\)
Test Statistic:
2-Sample Z-Test of Proportion:
It is used to compare whether the 2 independent samples differ in their proportions.
A company wants to compare its 2 different website designs A & B.
Below is the table that shows the data:
| Design | # of visitors(n) | # of signups(x) | conversion rate(\(\hat{p} = \frac{x}{n}\)) |
|---|---|---|---|
| A | 1000 | 80 | 0.08 |
| B | 1200 | 114 | 0.095 |
Is the design B better, i.e, design B increases conversion rate or proportion of visitors who sign up?
Consider the significance level of 5%.
Null Hypothesis: \(\hat{p_A} = \hat{p_B}\), i.e, no difference in conversion rates of 2 designs A & B.
Alternative Hypothesis: \(\hat{p_B} > \hat{p_A}\) i.e conversion rate of B > A => right tailed test.
Check large sample condition for both samples A & B.
\(n\hat{p_A} = 80 > 10 ~and~ n(1-\hat{p_A}) = 920 > 10\)
Similarly, we can show for B too.
Pooled proportion:
\[ \bar{p} = \frac{x_A+x_B}{n_A+n_B} = \frac{80+114}{1000+1200} = \frac{194}{2200} \\[10pt] => \bar{p}\approx 0.0882 \]Standard Error(Pooled):
\[ SE=\sqrt{\bar{p}(1-\bar{p})(\frac{1}{n_1} +\frac{1}{n_2})} \\[10pt] = \sqrt{0.0882(1-0.0882)(\frac{1}{1000} +\frac{1}{1200})} \\[10pt] => SE \approx 0.0123 \]Test Statistic(Z):
\[ t_{obs} = \frac{\hat{p_B}-\hat{p_A}}{SE_{\hat{p_A}-\hat{p_B}}} \\[10pt] = \frac{0.095-0.0882}{0.0123} \\[10pt] => t_{obs} \approx 1.22 \]Significance level \(\alpha\) = 5% =0.05.
Critical value \(Z_{0.05}\) = 1.645
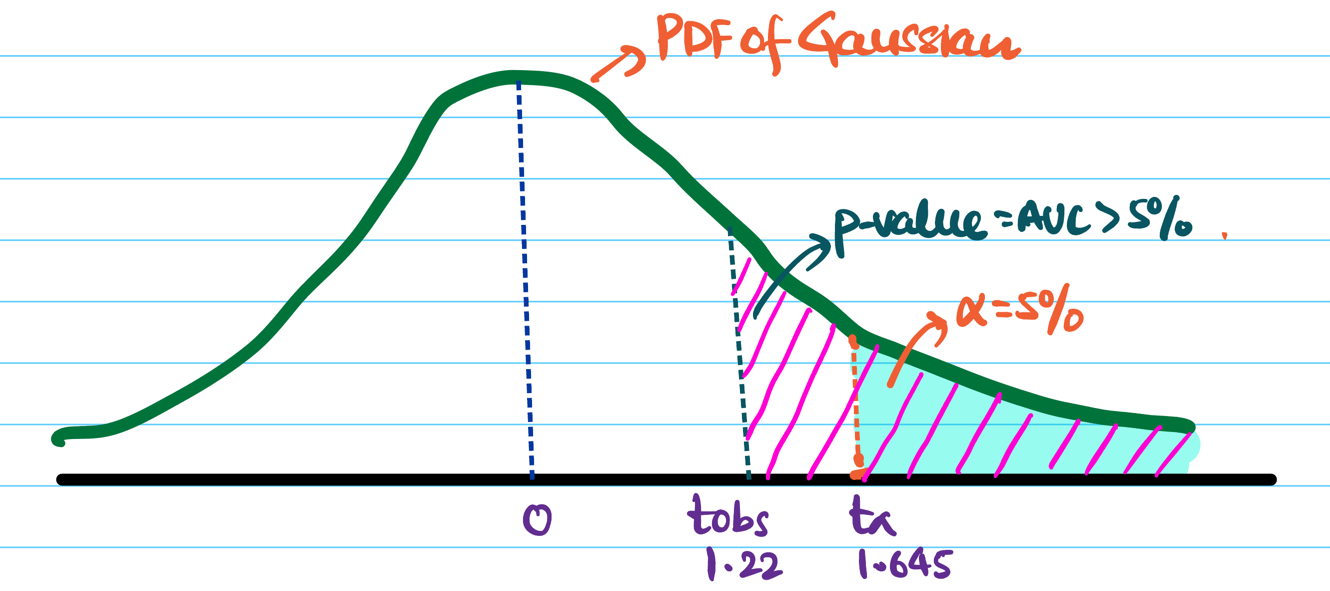
Since, \(t_{obs} < Z_{0.05}\) => p-value > 5%.
Hence, we fail to reject the null hypothesis.
Therefore, the observed conversion rate of design B is due to random chance; thus, B is not a better design.
End of Section
Chi-Square Distribution (\(\chi^2\)):
A random variable Q is said to follow a chi-square distribution with ’n’ degrees of freedom,i.e \(\chi^2(n)\),
if it is the sum of squares of ’n’ independent random variables that follow a standard normal distribution, i.e, \(N(0,1)\).
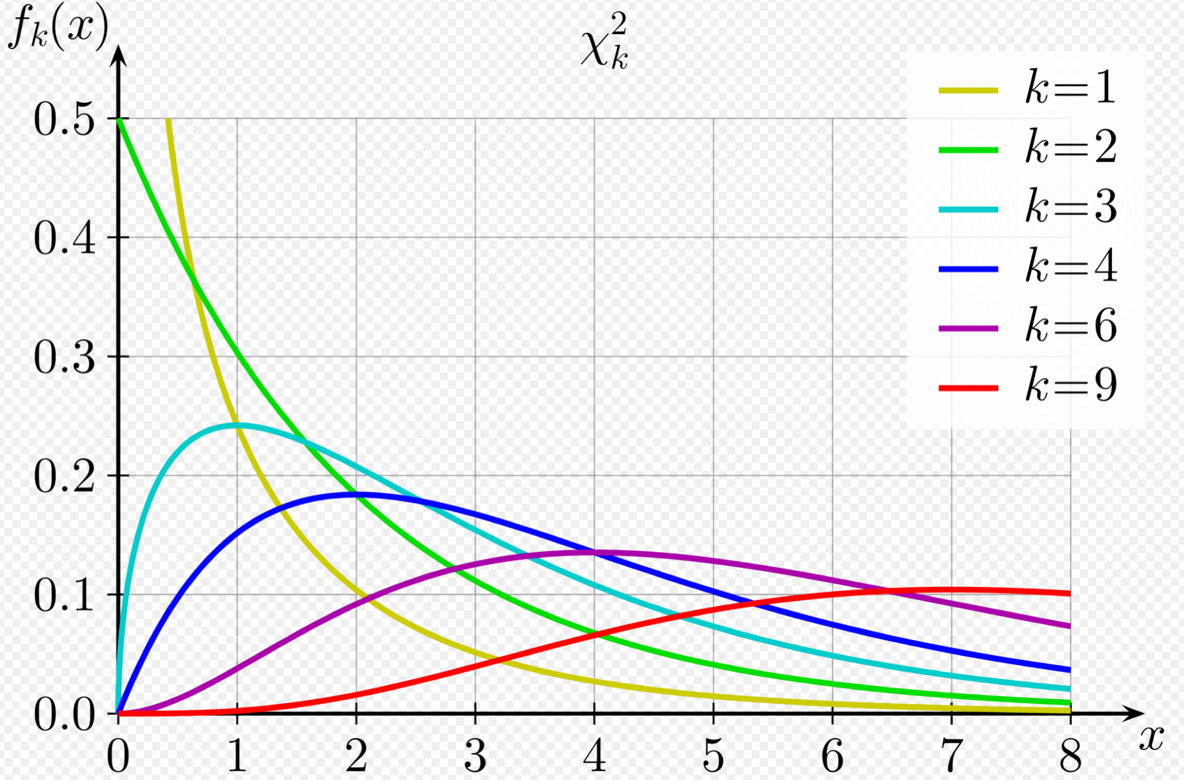
Key Properties:
Note: We are dealing with categorical data, where there is a count associated with each category.
In the context of categorical data, the counts \(O_i\) are governed by multinomial distribution
(a generalisation of binomial distribution).
Multinomial distribution is defined for multiple classes or categories, ‘k’, and multiple trials ’n’.
For \(i^{th}\) category:
Probability of \(i^{th}\) category = \(p_i\)
Mean = Expected count/frequency = \(E_i = np_i \)
Variance = \(Var_i = np_i(1-p_i) \)
By Central Limit Theorem, for very large n, i.e, as \(n \rightarrow \infty\), the multinomial distribution can be approximated as a normal distribution.
The multinomial distribution of count/frequency can be approximated as :
\(O_i \approx N(np_i, np_i(1-p_i))\)
Standardized count (mean centered and variance scaled):
Under Null Hypothesis:
In Pearson’s proof of the chi-square test, the statistic is divided by the expected value (\(E_{i}\)) instead of the variance (\(Var_{i}\)),
because for count data that can be modeled using a Poisson distribution
(or a multinomial distribution where cell counts are approximately Poisson for large samples),
the variance is equal to the expected value (mean).
Therefore, \(Z_i \approx (O_{i}-E_{i})/\sqrt{E_{i}}\)
Note that the denominator is \(\sqrt{E_{i}}\) NOT \(\sqrt{Var_{i}}\).
\(O_{i}\): Observed count for \(i^{th}\) category
\(E_{i}\): Expected count for \(i^{th}\) category
Important: \(E_{i}\): Expected count should be large i.e >= 5 (typically) for a good enough approximation.
Chi-Square (\(\chi^2\)) Test Statistic:
It is formed by squaring the approximately standard normal counts above, and summing them up.
For \(k\) categories, the test statistic is:
Note: For very large ’n’, the Pearson’s chi-square (\(\chi^2\)) test statistic follows a chi-square (\(\chi^2\)) distribution.
Test of Goodness of Fit:
It is used to compare the observed frequency distribution of a single categorical variable to a hypothesized or expected
probability distribution.
It can be used to determine whether a sample taken from a population follows a particular distribution,
e.g., uniform, normal, etc.
Test Statistic:
\(O_{i}\): Observed count for \(i^{th}\) category
\(E_{i}\): Expected count for \(i^{th}\) category, under null hypothesis \(H_0\)
\(k\): Number of categories
\(\nu\): Degrees of freedom = k - 1- m
\(m\): Number of parameters estimated from sample data to determine the expected probability
Note: Typical m=0, since, NO parameters are estimated.
We need to find whether the coin is fair i.e we need to do a goodness of fit test for discrete uniform distribution.
Null Hypothesis \(H_0\): Coin is fair.
Alternative Hypothesis \(H_a\): Coin is biased towards head.
\(O_{H}\): Observed count head = 62
\(O_{T}\): Observed count head = 38
\(E_{i}\): Expected count for \(i^{th}\) category, under null hypothesis \(H_0\) = 50 i.e fair coin
\(k\): Number of categories = 2
\(\nu\): Degrees of freedom = k - 1- m = 2 - 1 - 0 = 1
Test Statistic:
Since, significance level = 5% = 0.05
Critical value = \(\chi^2(0.05,1)\) = 3.84
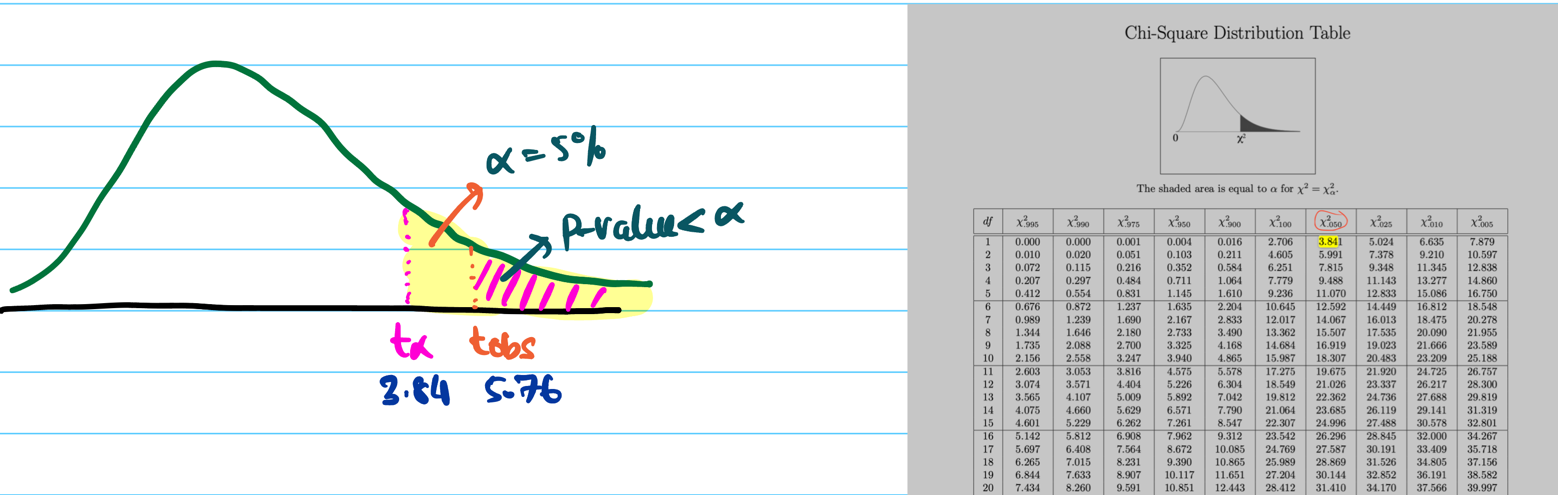
Since, \(t_{obs}\) = 5.76 > 3.84 (critical value), we reject the null hypothesis \(H_0\).
Therefore, the coin is biased towards head.
Test of Independence:
It is used to determine whether an association exists between two categorical variables,
using a contingency(dependency) table.
It is a non-parametric test, i.e, does NOT make any assumption about the underlying distribution of the data.
Test Statistic:
\(O_{ij}\): Observed count for \(cell_{i,j}\)
\(E_{ij}\): Expected count for \(cell_{i,j}\), under null hypothesis \(H_0\)
\(R\): Number of rows
\(C\): Number of columns
\(\nu\): Degrees of freedom = (R-1)*(C-1)
Let’s understand the above test statistic in more detail.
We know that, if 2 random variables A & B are independent, then,
\(P(A \cap B) = P(A, B) = P(A)*P(B)\)
i.e Joint Probability = Product of marginal probabilities.
Null Hypothesis \(H_0\): \(A\) and \(B\) are independent.
Alternative Hypothesis \(H_a\): \(A\) and \(B\) are dependent or associated.
N = Sample size
\(P(A_i) \approx \frac{Row ~~ Total_i}{N}\)
\(P(B_j) \approx \frac{Col ~~ Total_j}{N}\)
\(E_{ij}\) : Expected count for \(cell_{i,j}\) = \( N*P(A_i)*P(B_j)\)
=> \(E_{ij}\) = \(N*\frac{Row ~~ Total_i}{N}*\frac{Col ~~ Total_j}{N}\)
=> \(E_{ij}\) = \(\frac{Row ~~ Total_i * Col ~~ Total_j}{N}\)
\(O_{ij}\): Observed count for \(cell_{i,j}\)
A survey of 100 students was conducted to understand whether there is any relation between gender and beverage preference.
Below is the table that shows the number of students who prefer each beverage.
| Gender | Tea | Coffee | |
|---|---|---|---|
| Male | 20 | 30 | 50 |
| Female | 10 | 40 | 50 |
| 30 | 70 |
Significance level = 5%
Null Hypothesis \(H_0\): Gender and beverage preference are independent.
Alternative Hypothesis \(H_a\): Gender and beverage preference are dependent.
We know that Expected count for cell(i,j) = \(E_{ij}\) = \(\frac{Row ~~ Total_i * Col ~~ Total_j}{N}\)
\(E_{11} = \frac{50*30}{100} = 15\)
\(E_{12} = \frac{50*70}{100} = 35\)
\(E_{21} = \frac{50*30}{100} = 15\)
\(E_{22} = \frac{50*70}{100} = 35\)
Test Statistic:
Degrees of freedom = (R-1)(C-1) = (2-1)(2-1) = 1
Since, significance level = 5% = 0.05
Critical value = \(\chi^2(0.05,1)\) = 3.84
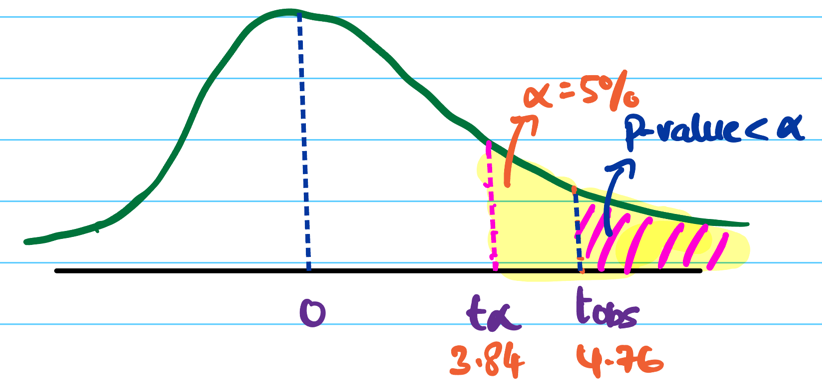
Since, \(t_{obs}\) = 4.76 > 3.84 (critical value), we reject the null hypothesis \(H_0\).
Therefore, the gender and beverage preference are dependent.
End of Section
Confusion Matrix:
It is a table that summarizes model’s predictions against the actual class labels, detailing where the model
succeeded and where it failed.
It is used for binary or multi-class classification problems.
| Predicted Positive | Predicted Negative | |
|---|---|---|
| Actual Positive | True Positive (TP) | False Negative (FN) |
| Actual Negative | False Positive (FP) | True Negative (TN) |
Type-1 Error:
It is the number of false positives.
e.g.: Model predicted that a patient has diabetes, but the patient actually does NOT have diabetes; “false alarm”.
Type-2 Error:
It is the number of false negatives.
e.g.: Model predicted that a patient does NOT have diabetes, but the patient actually has diabetes; “a miss”.
Many metrics are derived from the confusion matrix.
Precision:
It answers the question: “Of all the instances that the model predicted as positive, how many were actually positive?”
It measures exactness or quality of the positive predictions.
Recall:
It answers the question: “Of all the actual positive instances, how many did the model correctly identify?”
It measures completeness or coverage of the positive predictions.
F1 Score:
It is the harmonic mean of precision and recall.
It is used when we need a balance between precision and recall; also helpful when we have imbalanced data.
Harmonic mean penalizes extreme values more heavily, encouraging both metrics to be high.
| Precision | Recall | F1 Score | Mean |
|---|---|---|---|
| 0.5 | 0.5 | 0.50 | 0.5 |
| 0.7 | 0.3 | 0.42 | 0.5 |
| 0.9 | 0.1 | 0.18 | 0.5 |
Trade-Off:
Precision Focus:: Critical when cost of false positives is high.
e.g: Identify a potential terrorist.
A false positive, i.e, wrongly flagging an innocent person as a potential terrorist is very harmful.
Recall Focus:: Critical when cost of false negatives is high.
e.g.: Medical diagnosis of a serious disease.
A false negative, i.e, falsely missing a serious disease can cost someone’s life.
Analyze the performance of an access control system. Below is the data for 1000 access attempts.
| Predicted Authorised Access | Predicted Unauthorised Access | |
|---|---|---|
| Actual Authorised Access | 90 (TP) | 10 (FN) |
| Actual Unauthorised Access | 1 (FP) | 899 (TN) |
When the system allows access, it is correct 98.9% of the time.
The system caught 90% of all authorized accesses.
Receiver Operating Characteristic (ROC) Curve:
It is a graphical plot that shows the discriminating ability of a binary classifier system, as its
discrimination threshold is varied.
Y-axis: True Positive Rate (TPR), Recall, Sensitivity
\(TPR = \frac{TP}{TP + FN}\)
X-axis: False Positive Rate (FPR); (1 - Specificity)
\(FPR = \frac{FP}{FP + TN}\)
Note: A binary classifier model outputs a probability score between 0 and 1.
and a threshold (default=0.5) is applied to the probability score to get the final class label.
\(p \ge 0.5\) => Positive Class
\(p < 0.5\) => Negative Class
Algorithm:
e.g.:
| Patient_Id | True Label \(y_i\) | Predicted Probability Score \(\hat{y_i}\) |
|---|---|---|
| 1 | 1 | 0.95 |
| 2 | 0 | 0.85 |
| 3 | 1 | 0.72 |
| 4 | 1 | 0.63 |
| 5 | 0 | 0.59 |
| 6 | 1 | 0.45 |
| 7 | 1 | 0.37 |
| 8 | 0 | 0.20 |
| 9 | 0 | 0.12 |
| 10 | 0 | 0.05 |
Set the threshold \(\tau_1\) = 0.95, calculate \({TPR}_1, {FPR}_1\)
Set the threshold \(\tau_2\) = 0.85, calculate \({TPR}_2, {FPR}_2\)
Set the threshold \(\tau_3\) = 0.72, calculate \({TPR}_3, {FPR}_3\)
…
…
Set the threshold \(\tau_n\) = 0.05, calculate \({TPR}_n, {FPR}_n\)
Now, we have ’n’ pairs of (TPR, FPR) for all ’n’ data points.
Plot the points on a graph to get the final ROC curve.
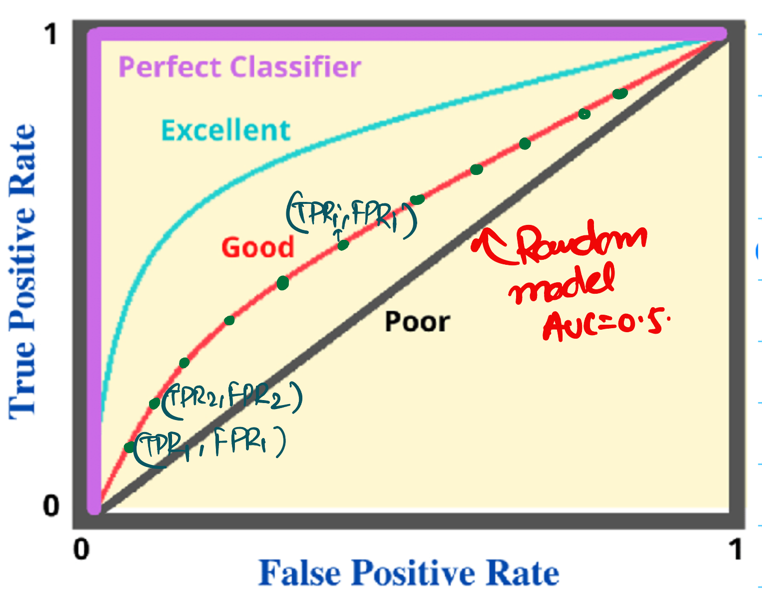
AU ROC = AUC = Area under the ROC curve = Area under the curve
Note:
Let’s understand this with the below fraud detection example.
Below is a dataset from a fraud detection system for N = 10,000 transactions.
Fraud = 100, NOT fraud = 9900
| Predicted Fraud | Predicted NOT Fraud | |
|---|---|---|
| Actual Fraud | 80 (TP) | 20 (FN) |
| Actual NOT Fraud | 220 (FP) | 9680 (TN) |
If we check the location of above (TPR, FPR) pair on the ROC curve, then we can see that it is
very close to the top-left corner.
This means that the model is very good at detecting fraudulent transactions, but that is NOT the case.
This is happening because of the imbalanced data, i.e, count of NOT fraud transactions is 99 times
of fraudulent transactions.
Let’s look at the Precision value:
We can see that the model has poor precision,i.e, only 26.7% of flagged transactions are actual frauds.
Unacceptable precision for a good fraud detection system.
Precision-Recall Curve:
It is used to evaluate the performance of a binary classifier model across various thresholds.
It is similar to the ROC curve, but it uses Precision instead of TPR on the Y-axis.
Plots Precision (Y-axis) against Recall (X-axis) for different classification thresholds.
Note: It is useful when the data is imbalanced.
AU PRC = PR AUC = Area under Precision-Recall curve
Let’s revisit the fraud detection example discussed above to understand the utility of PR curve.
| Predicted Fraud | Predicted NOT Fraud | |
|---|---|---|
| Actual Fraud | 80 (TP) | 20 (FN) |
| Actual NOT Fraud | 220 (FP) | 9680 (TN) |
If we check the location of above (Precision, Recall) point on PRC curve, we will find that it is located near the
bottom right corner, i.e, the model performance is poor.
End of Section
This sheet contains all the topics that will be covered for Linear Algebra for AI & ML.
Vector:
It is a collection of scalars(numbers) that has both magnitude and direction.
Geometrically, it is a line segment in space characterized by its length(magnitude) and direction.
By convention, we represent vectors as column vectors.
e.g.:
\(\vec{x} = \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}_{\text{n×1}}\) i.e ’n’ rows and 1 column.
Important: In machine learning, we will use bold notation \(\mathbf{v}\) to represent vectors, instead
of arrow notation \(\mathbf{v}\).
Transpose:
Swap the rows and columns, i.e, a column vector becomes a row vector after transpose.
e.g:
\(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_d \end{bmatrix}_{\text{d×1}}\)
\(\mathbf{v}^\mathrm{T} = \begin{bmatrix} v_1 & v_2 & \cdots & v_d \end{bmatrix}_{\text{1×d}}\)
Length of Vector:
The length (or magnitude or norm) of a vector \(\mathbf{v}\) is the distance from the origin to the point represented
by \(\mathbf{v}\) in n-dimensional space.
\(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_d \end{bmatrix}_{\text{d×1}}\)
Length of vector:
Note: The length of a zero vector is 0.
Direction of Vector:
The direction of a vector tells us where the vector points in space, independent of its length.
Direction of vector:
\[\mathbf{v} = \frac{\vec{v}} {\|\mathbf{v}\|} \]Vector Space:
It is a collection of vectors that can be added together and scaled by numbers (scalars), such that,
the results are still in the same space.
Vector space or linear space is a non-empty set of vectors equipped with 2 operations:
e.g.: Set of all points in 2D is a vector space.
Addition:
We can only add vectors of the same dimension.
e.g: lets add 2 real d-dimensional vectors, \(\mathbf{u} , \mathbf{v} \in \mathbb{R}^{d \times 1}\):
\(\mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_d \end{bmatrix}_{\text{d×1}}\),
\(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_d \end{bmatrix}_{\text{d×1}}\)
\(\mathbf{u} + \mathbf{v} = \begin{bmatrix} u_1+v_1 \\ u_2+v_2 \\ \vdots \\ u_d+v_d \end{bmatrix}_{\text{d×1}}\)
Multiplication:
1. Multiplication with Scalar:
All elements of the vector are multiplied with the scalar.
e.g:
\(\alpha\mathbf{v} = \begin{bmatrix} \alpha v_1 \\ \alpha v_2 \\ \vdots \\ \alpha v_d \end{bmatrix}_{\text{d×1}}\)
2.Inner (Dot) Product:
Inner(dot) product \(\mathbf{u} \cdot \mathbf{v}\) of 2 vectors gives a scalar output.
The two vectors must be of the same dimensions.
Dot product:
\(\mathbf{u} \cdot \mathbf{v} = \mathbf{u}^\mathrm{T} \mathbf{v}\)
= \(\begin{bmatrix} u_1 & u_2 & \cdots & u_d \end{bmatrix}_{\text{1×d}}
\cdot
\begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_d
\end{bmatrix}_{\text{d×1}} = u_1v_1 + u_2v_2 + \cdots + u_dv_d\)
Geometrically, \(\mathbf{u} \cdot \mathbf{v}\) = \(|u||v|cos\theta\)
where \(\theta\) is the angle between \(\mathbf{u}\) and \(\mathbf{v}\).
\(\mathbf{u} = \begin{bmatrix} 1 \\ \\ 2 \\ \end{bmatrix}_{\text{2×1}}\), \(\mathbf{v} = \begin{bmatrix} 3 \\ \\ 4 \\ \end{bmatrix}_{\text{2×1}}\)
\(\mathbf{u} \cdot \mathbf{v}\) = \(|u||v|cos\theta = 1 \times 3 + 2 \times 4 = 11\)
2.Outer (Tensor) Product:
Outer (tensor) product \(\mathbf{u} \otimes \mathbf{v}\) of 2 vectors gives a matrix output.
The two vectors must be of the same dimensions.
Tensor product:
\(\mathbf{u} \otimes \mathbf{v} = \mathbf{u} \mathbf{v}^\mathrm{T} \)
= \(\begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_d \end{bmatrix}_{\text{d×1}}
\otimes
\begin{bmatrix} v_1 & v_2 & \cdots & v_d \end{bmatrix}_{\text{1×d}}
= \begin{bmatrix}
u_1v_1 & u_1v_2 & \cdots & u_1v_d \\
u_2v_1 & u_2v_2 & \cdots & u_2v_n \\
\vdots & \vdots & \ddots & \vdots \\
u_dv_1 & u_dv_2 & \cdots & u_dv_d
\end{bmatrix}
\in \mathbb{R}^{d \times d}\)
e.g:
\(\mathbf{u} = \begin{bmatrix} 1 \\ \\ 2 \\ \end{bmatrix}_{\text{2×1}}\),
\(\mathbf{v} = \begin{bmatrix} 3 \\ \\ 4 \\ \end{bmatrix}_{\text{2×1}}\)
\(\mathbf{u} \otimes \mathbf{v} = \mathbf{u} \mathbf{v}^\mathrm{T} \) = \(\begin{bmatrix} 1 \\ \\ 2 \\ \end{bmatrix}_{\text{2×1}} \otimes \begin{bmatrix} 3 & 4 \end{bmatrix}_{\text{1×2}} = \begin{bmatrix} 1 \times 3 & 1 \times 4 \\ \\ 2 \times 3 & 2 \times 4 \\ \end{bmatrix} _{\text{2×2}} = \begin{bmatrix} 3 & 4 \\ \\ 6 & 8 \\ \end{bmatrix} _{\text{2×2}}\)
Note: We will NOT discuss about cross product \(\mathbf{u} \times \mathbf{v}\); product perpendicular to both vectors.
Linear Independence:
A set of vectors are linearly independent if NO vector in the set can be expressed as a linear combination of
the other vectors in the set.
The only solution for :
\(\alpha_1 \mathbf{u}_1 + \alpha_2 \mathbf{u}_2 + \cdots + \alpha_k \mathbf{u}_k\) = 0
is \(\alpha_1 = \alpha_2, \cdots, = \alpha_k = 0\).
e.g.:
The below 3 vectors are linearly independent.
\(\mathbf{u} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}_{\text{3×1}}\),
\(\mathbf{v} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix}_{\text{3×1}}\),
\(\mathbf{w} = \begin{bmatrix} 1 \\ 3 \\ 6 \\ \end{bmatrix}_{\text{3×1}}\)
The below 3 vectors are linearly dependent.
\(\mathbf{u} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}_{\text{3×1}}\),
\(\mathbf{v} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix}_{\text{3×1}}\),
\(\mathbf{w} = \begin{bmatrix} 2 \\ 4 \\ 6 \\ \end{bmatrix}_{\text{3×1}}\)
because, \(\mathbf{w} = 2\mathbf{v}\), and we have a non-zero solution for the below equation:
\(\alpha_1 \mathbf{u} + \alpha_2 \mathbf{v} + \alpha_3 \mathbf{w} = 0\);
\(\alpha_1 = 0, \alpha_2 = -2, \alpha_3 = 1\) is a valid non-zero solution.
Note:
Span:
Span of a set of vectors is the geometric shape by all possible linear combinations of those vectors, such as,
line, plane, or higher dimensional volume.
e.g.:
Basis:
It is the minimal set of linearly independent vectors that spans or defines the entire vector space,
providing a unique co-ordinate system for every vector within the space.
Every vector in the vector space can be represented as a unique linear combination of the basis vectors.
e.g.:
Note: Basis = Dimensions
Orthogonal Vectors:
Two vectors are orthogonal if their dot product is 0.
A set of vectors \(\mathbf{x_1}, \mathbf{x_2}, \cdots ,\mathbf{x_n} \) are said to be orthogonal if:
\(\mathbf{x_i} \cdot \mathbf{x_j} = 0 \forall i⍯j\), for every pair, i.e, every pair must be orthogonal.
e.g.:
Note:
Orthogonal vectors are linearly independent, but the inverse may NOT be true,
i.e, linear independence does NOT imply that vectors are orthogonal.
e.g.:
Vectors \(\mathbf{u} = (2,0)\) and \(\mathbf{v} = (1,3) \) are linearly independent but NOT orthogonal.
Since, \(\mathbf{u} \cdot \mathbf{v} = 2*1 + 3*0 = 2 ⍯ 0\).
Orthogonality is the most extreme case of linear independence, i.e \(90^{\degree}\) apart or perpendicular.
Orthonormal Vectors:
Orthonormal vectors are vectors that are orthogonal and have unit length.
A set of vectors \(\mathbf{x_1}, \mathbf{x_2}, \cdots ,\mathbf{x_n} \) are said to be orthonormal if:
\(\mathbf{x_i} \cdot \mathbf{x_j} = 0 \forall i⍯j\) and \(\|\mathbf{x_i}\| = 1\), i.e, unit vector.
e.g.:
Orthonormal Basis:
It is a set of vectors that functions as a basis for a space while also being orthonormal,
meaning each vector is a unit vector (has a length of 1) and all vectors are mutually perpendicular (orthogonal) to each other.
A set of vectors \(\mathbf{x_1}, \mathbf{x_2}, \cdots ,\mathbf{x_n} \) are said to be orthonormal basis of a vector space
\(\mathbb{R}^{n \times 1}\), if every vector:
e.g.:
Note: In a n-dimensional space, there are only \(n\) possible orthonormal bases.
End of Section
Matrices let us store, manipulate, and transform data efficiently.
e.g:
Matrix
It is a two-dimensional array of numbers with a fixed number of rows(m) and columns(n).
e.g:
\(
\mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix}
_{\text{m x n}}
\)
Transpose:
Swapping rows and columns of a matrix.
\(
\mathbf{A}^T =
\begin{bmatrix}
a_{11} & a_{21} & \cdots & a_{m1} \\
a_{12} & a_{22} & \cdots & a_{m2} \\
\vdots & \vdots & \ddots & \vdots \\
a_{1n} & a_{2n} & \cdots & a_{mn}
\end{bmatrix}
_{\text{n x m}}
\)
Important: \( (AB)^T = B^TA^T \)
Rank:
Rank of a matrix is the number of linearly independent rows or columns of the matrix.
Addition:
We add two matrices by adding the corresponding elements.
They must have same dimensions.
\( \mathbf{A} + \mathbf{B} =
\begin{bmatrix}
a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\
a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2n} + b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn}
\end{bmatrix}
_{\text{m x n}}
\)
Multiplication:
We can multiply two matrices only if their inner dimensions are equal.
\( \mathbf{C}_{m x n} = \mathbf{A}_{m x d} ~ \mathbf{B}_{d x n} \)
\( c_{ij} \) = Dot product of \(i^{th}\) row of A and \(j^{th}\) row of B.
\( c_{ij} = \sum_{k=1}^{d} A_{ik} * B_{kj} \)
=> \( c_{11} = a_{11} * b_{11} + a_{12} * b_{21} + \cdots + a_{1d} * b_{d1} \)
e.g:
\(
\mathbf{A} =
\begin{bmatrix}
1 & 2 \\
\\
3 & 4
\end{bmatrix}
_{\text{2 x 2}},
\mathbf{B} =
\begin{bmatrix}
5 & 6 \\
\\
7 & 8
\end{bmatrix}
_{\text{2 x 2}}
\)
\(
\mathbf{C} = \mathbf{A} \times \mathbf{B} =
\begin{bmatrix}
1 * 5 + 2 * 7 & 1 * 6 + 2 * 8 \\
\\
3 * 5 + 4 * 7 & 3 * 6 + 4 * 8
\end{bmatrix}
_{\text{2 x 2}}
= \begin{bmatrix}
19 & 22 \\
\\
43 & 50
\end{bmatrix}
_{\text{2 x 2}}
\)
Key Properties:
Square Matrix:
It is a matrix with same number of rows and columns (m=n).
\(
\mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
_{\text{n x n}}
\)
Diagonal Matrix:
It is a square matrix with all non-diagonal elements equal to zero.
e.g.:
\( \mathbf{D} =
\begin{bmatrix}
d_{11} & 0 & \cdots & 0 \\
0 & d_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_{nn}
\end{bmatrix}
_{\text{n x n}}
\)
Note: Product of 2 diagonal matrices is a diagonal matrix.
Lower Triangular Matrix:
It is a square matrix with all elements above the diagonal equal to zero.
e.g.:
\( \mathbf{L} =
\begin{bmatrix}
l_{11} & 0 & \cdots & 0 \\
l_{21} & l_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
l_{n1} & l_{n2} & \cdots & l_{nn}
\end{bmatrix}
_{\text{n x n}}
\)
Note: Product of 2 lower triangular matrices is an lower triangular matrix.
Upper Triangular Matrix:
It is a square matrix with all elements below the diagonal equal to zero.
e.g.:
\( \mathbf{U} =
\begin{bmatrix}
u_{11} & u_{12} & \cdots & u_{1n} \\
0 & u_{22} & \cdots & u_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & u_{nn}
\end{bmatrix}
_{\text{n x n}}
\)
Note: Product of 2 upper triangular matrices is an upper triangular matrix.
Symmetric Matrix:
It is a square matrix that is equal to its own transpose, i.e, flip the matrix along its diagonal,
it remains unchanged.
\( \mathbf{A} = \mathbf{A}^T \)
e.g.:
\( \mathbf{S} =
\begin{bmatrix}
s_{11} & s_{12} & \cdots & s_{1n} \\
s_{12} & s_{22} & \cdots & s_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
s_{1n} & s_{2n} & \cdots & s_{nn}
\end{bmatrix}
_{\text{n x n}}
\)
Note: Diagonal matrix is a symmetric matrix.
Skew Symmetric Matrix:
It is a square symmetric matrix where the elements across the diagonal have opposite signs.
Also called Anti Symmetric Matrix.
\( \mathbf{A} = -\mathbf{A}^T \)
e.g.:
\( \mathbf{S} =
\begin{bmatrix}
0 & s_{12} & \cdots & s_{1n} \\
-s_{12} & 0 & \cdots & s_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
-s_{1n} & -s_{2n} & \cdots & 0
\end{bmatrix}
_{\text{n x n}}
\)
Note: Diagonal elements of a skew symmetric matrix are zero, since the number should be equal to its negative.
Identity Matrix:
It is a square matrix with all the diagonal values equal to 1, rest of the elements are equal to zero.
e.g.:
\( \mathbf{I} =
\begin{bmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{bmatrix}
_{\text{n x n}}
\)
Important:
\( \mathbf{I} \times \mathbf{A} = \mathbf{A} \times \mathbf{I} = \mathbf{A} \)
Trace:
It is the sum of the elements on the main diagonal of a square matrix.
Note: Main diagonal is NOT defined for a rectangular matrix.
\( \text{trace}(A) = \sum_{i=1}^{n} a_{ii} = a_{11} + a_{22} + \cdots + a_{nn}\)
If \( \mathbf{A} \in \mathbb{R}^{m \times n} \), and \( \mathbf{B} \in \mathbb{R}^{n \times m} \), then
\( \text{trace}(AB)_{m \times m} = \text{trace}(BA)_{n \times n} \)
Determinant:
It is a scalar value that reveals crucial properties about the matrix and its linear transformation.
\(a_{1j} \) = element in the first row and j-th column
\(M_{1j} \) = submatrix of the matrix excluding the first row and j-th column
If n = 2, then,
\( |A| = a_{11} \, a_{22} - a_{12} \, a_{21} \)
Singular Matrix:
A square matrix with linearly dependent rows or columns, i.e, determinant = 0.
A singular matrix collapses space, say, a 3D space, into a 2D space or a higher dimensional space
to a lower dimensional space, making the transformation impossible to reverse.
Hence, a singular matrix is NOT invertible; i.e, inverse does NOT exist.
Singular matrix is also NOT invertible, because the inverse has division by determinant, and its determinant is zero.
Also called rank deficient matrix, because the rank < number of dimensions of the matrix,
due to the presence of linearly dependent rows or columns.
e.g: Below is a linearly dependent 2x2 matrix.
\( \mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} \\
\\
\beta a_{11} & \beta a_{12}
\end{bmatrix}
_{\text{2 x 2}},
det(\mathbf{A}) =
a_{11}\cdot \beta a_{12} - a_{12} \cdot \beta a_{11} = 0
\)
Note:
Inverse:
It is a square matrix that when multiplied by the original matrix, gives the identity matrix.
\( \mathbf{A} \mathbf{A}^{-1} = \mathbf{A}^{-1} \mathbf{A} = \mathbf{I} \)
Steps to compute inverse of a matrix:
e.g:
\(
\mathbf{A} =
\begin{bmatrix}
1 & 0 & 3\\
2 & 1 & 1\\
1 & 1 & 1 \\
\end{bmatrix}
_{\text{3 x 3}}
\),
Co-factor matrix:
\(
\mathbf{C} =
\begin{bmatrix}
0 & -1 & 1\\
3 & -2 & -1\\
-3 & 5 & 1 \\
\end{bmatrix}
_{\text{3 x 3}}
\)
Adjugate matrix, adj(A) =
\(
\mathbf{C}^\mathrm{T} =
\begin{bmatrix}
0 & 3 & -3\\
-1 & -2 & 5\\
1 & -1 & 1 \\
\end{bmatrix}
_{\text{3 x 3}}
\)
determinant of \( \mathbf{A} \) =
\(
\begin{vmatrix}
1 & 0 & 3\\
2 & 1 & 1\\
1 & 1 & 1 \\
\end{vmatrix}
= 0 -\cancel 1 + \cancel 1 + \cancel3 - 2 -\cancel1 -\cancel 3 + 5 + \cancel1 = 3
\)
\(
\mathbf{A}^{-1} = \frac{1}{|A|}\,\mathrm{adj}(A)
= \frac{1}{3}\,
\begin{bmatrix}
0 & 3 & -3\\
-1 & -2 & 5\\
1 & -1 & 1 \\
\end{bmatrix}
_{\text{3 x 3}}
\)
=> \(
\mathbf{A}^{-1} =
\begin{bmatrix}
0 & 1 & -1\\
-1/3 & -2/3 & 5/3\\
1/3 & -1/3 & 1/3 \\
\end{bmatrix}
_{\text{3 x 3}}
\)
Note:
Orthogonal Matrix:
It is a square matrix that whose rows and columns are orthonormal vectors, i.e, they are perpendicular to each other
and have a unit length.
\( \mathbf{A} \mathbf{A}^\mathrm{T} = \mathbf{A}^\mathrm{T} \mathbf{A} = \mathbf{A} \mathbf{A}^{-1} = \mathbf{I} \)
=> \( \mathbf{A}^\mathrm{T} = \mathbf{A}^{-1} \)
Note:
Let’s check out why the rows and columns of an orthogonal matrix are orthonormal.
\( \mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} \\
\\
a_{21} & a_{22}
\end{bmatrix}
_{\text{2 x 2}}
\),
=> \( \mathbf{A}^\mathrm{T} =
\begin{bmatrix}
a_{11} & a_{21} \\
\\
a_{12} & a_{22}
\end{bmatrix}
_{\text{2 x 2}}
\)
Since, \( \mathbf{A} \mathbf{A}^\mathrm{T} = \mathbf{I} \)
\(
\begin{bmatrix}
a_{11} & a_{12} \\
\\
a_{21} & a_{22}
\end{bmatrix}
\begin{bmatrix}
a_{11} & a_{21} \\
\\
a_{12} & a_{22}
\end{bmatrix}
= \begin{bmatrix}
a_{11}^2 + a_{12}^2 & a_{11}a_{21} + a_{12}a_{22} \\
\\
a_{21}a_{11} + a_{21}a_{12} & a_{21}^2 + a_{22}^2
\end{bmatrix}
= \begin{bmatrix}
1 & 0 \\
\\
0 & 1
\end{bmatrix}
\)
Equating the terms, we get:
\( a_{11}^2 + a_{12}^2 = 1 \) => row 1 is a unit vector
\( a_{21}^2 + a_{22}^2 = 1 \) => row 2 is a unit vector
\( a_{11}a_{21} + a_{12}a_{22} = 0 \) => row 1 and row 2 are orthogonal to each other, since dot product = 0
\( a_{21}a_{11} + a_{21}a_{12} = 0 \) => row 1 and row 2 are orthogonal to each other, since dot product = 0
Therefore, the rows and columns of an orthogonal matrix are orthonormal.
Let, \(\mathbf{Q}\) is an orthogonal matrix, and \(\mathbf{v}\) is a vector.
Let’s calculate the length of \( \mathbf{Q} \mathbf{v} \)
Therefore, linear transformation of a vector by an orthogonal matrix does NOT change its length.
Lets solve the system of equations using matrix:
\(\begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix}
\)
\(
\begin{bmatrix}
x \\
\\
y
\end{bmatrix}
= \begin{bmatrix}
5 \\
\\
4
\end{bmatrix}
\)
The above equation can be written as:
\(\mathbf{AX} = \mathbf{B} \)
=> \( \mathbf{X} = \mathbf{A}^{-1} \mathbf{B} \)
\( \mathbf{A} = \begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix},
\mathbf{B} = \begin{bmatrix}
5 \\
\\
4
\end{bmatrix},
\mathbf{X} = \begin{bmatrix}
x \\
\\
y
\end{bmatrix}
\)
Lets compute the inverse of A matrix:
\( \mathbf{A}^{-1} = \frac{1}{3}\begin{bmatrix}
2 & -1 \\
\\
-1 & 2
\end{bmatrix}
\)
Since, \( \mathbf{X} = \mathbf{A}^{-1} \mathbf{B} \)
=> \( \mathbf{X} = \begin{bmatrix}
x \\
\\
y
\end{bmatrix}
= \frac{1}{3}\begin{bmatrix}
2 & -1 \\
\\
-1 & 2
\end{bmatrix}
\begin{bmatrix}
5 \\
\\
4
\end{bmatrix}
= \frac{1}{3}\begin{bmatrix}
6 \\
\\
3
\end{bmatrix}
= = \begin{bmatrix}
2 \\
\\
1
\end{bmatrix}
\)
Therefore, \( x = 2 \) and \( y = 1 \).
End of Section
\(\mathbf{Au} = \begin{bmatrix} 1 \\ \\ 2 \\ \end{bmatrix}\) , \(\quad\)
\(\mathbf{Av} = \begin{bmatrix} 3 \\ \\ 3 \\ \end{bmatrix}\)
Since, for an eigen vector, result of linear transformation, i.e, multiplying the vector by a matrix, is just a scalar multiple of the original vector, =>
\[ \mathbf{A} \mathbf{v} = \lambda \mathbf{v} \\ \mathbf{A} \mathbf{v} - \lambda \mathbf{v} = 0 \\ \mathbf{v}(\mathbf{A} - \lambda \mathbf{I}) = 0 \\ \]For a non-zero eigen vector, \((\mathbf{A} - \lambda \mathbf{I})\) must be singular, i.e,
\(det(\mathbf{A} - \lambda \mathbf{I}) = 0 \)
If, \( \mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
_{\text{n x n}}
\),
then, \((\mathbf{A} - \lambda \mathbf{I}) =
\begin{bmatrix}
a_{11}-\lambda & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22}-\lambda & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}-\lambda
\end{bmatrix}
_{\text{n x n}}
\)
\(det(\mathbf{A} - \lambda \mathbf{I})) = 0 \), will give us a polynomial equation in \(\lambda\) of degree \(n\),
we need to solve this polynomial equation to get the \(n\) eigen values.
e.g.:
\( \mathbf{A} = \begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix}
\),
\( \quad det(\mathbf{A} - \lambda \mathbf{I})) = 0 \quad \) =>
\( det \begin{bmatrix}
2-\lambda & 1 \\
\\
1 & 2-\lambda
\end{bmatrix} = 0
\)
\( (2-\lambda)^2 - 1 = 0\)
\( => |\lambda - 2| = \pm 1 \)
\( => \lambda_1 = 3\) and \( \lambda_2 = 1\)
Therefore, eigen vectors corresponding to eigen values \(\lambda_1 = 3\) and \( \lambda_2 = 1\) are:
\((\mathbf{A} - \lambda \mathbf{I}) \mathbf{v} = 0 \)
\(\lambda_1 = 3\)
=>
\(
\begin{bmatrix}
2-3 & 1 \\
\\
1 & 2-3
\end{bmatrix} \begin{bmatrix} v_1 \\ \\ v_2 \\ \end{bmatrix} =
\begin{bmatrix}
-1 & 1 \\
\\
1 & -1
\end{bmatrix} \begin{bmatrix} v_1 \\ \\ v_2 \\ \end{bmatrix} = 0
\)
=> Both the equations will be \(v_1 - v_2 = 0 \), i.e, \(v_1 = v_2\)
So, we can choose any vector, where x-axis and y-axis components are same, i.e, \(v_1 = v_2\)
=> Eigen vector: \(v_1 = \begin{bmatrix} 1 \\ \\ 1 \\ \end{bmatrix}\)
Similarly, for \(\lambda_2 = 1\)
we will get, eigen vector: \(v_2 = \begin{bmatrix} 1 \\ \\ -1 \\ \end{bmatrix}\)
\(tr(\mathbf{A}) = 2 + 2 = 3 + 1 = 4\)
\(det(\mathbf{A}) = 2 \times 2 - 1 \times 1 = 3 \times 1 = 3 \)
Let’ calculate the 2nd power of a square matrix.
e.g.:
\(\mathbf{A} = \begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix}
\),
\(\quad \mathbf{A}^2 = \begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix} \begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix} = \begin{bmatrix}
5 & 4 \\
\\
4 & 5
\end{bmatrix}
\)
Let’s calculate the 2nd power of a diagonal matrix.
e.g.:
\(\mathbf{A} = \begin{bmatrix}
3 & 0 \\
\\
0 & 2
\end{bmatrix}
\),
\(\quad \mathbf{A}^2 = \begin{bmatrix}
3 & 0 \\
\\
0 & 2
\end{bmatrix} \begin{bmatrix}
3 & 0 \\
\\
0 & 2
\end{bmatrix} = \begin{bmatrix}
9 & 0 \\
\\
0 & 4
\end{bmatrix}
\)
Note that when we square the diagonal matrix, then all the diagonal elements got squared.
Similarly, if we want to calculate the kth power of a diagonal matrix, then all we need to do is to just compute the kth
powers of all diagonal elements, instead of complex matrix multiplications.
\(\quad \mathbf{A}^k = \begin{bmatrix}
3^k & 0 \\
\\
0 & 2^k
\end{bmatrix}
\)
Therefore, if we diagonalize a square matrix then the computation of power of the matrix will become very easy.
Next, let’s see how to diagonalize a matrix.
\(\mathbf{V}\): Matrix of all eigen vectors(as columns) of matrix \(\mathbf{A}\)
\( \mathbf{V} = \begin{bmatrix}
\mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_n \\
\vdots & \vdots & \ddots & \vdots \\
\vdots & \vdots & \vdots & \vdots\\
\end{bmatrix}
\),
where, each column is an eigen vector corresponding to an eigen value \(\lambda_i\).
If \( \mathbf{v}_1 \mathbf{v}_2 \cdots \mathbf{v}_n \) are linearly independent, then,
\(det(\mathbf{V}) ~⍯ ~ 0\).
=> \(\mathbf{V}\) is NOT singular and \(\mathbf{V}^{-1}\) exists.
\(\Lambda\): Diagonal matrix of all eigen values of matrix \(\mathbf{A}\)
\( \Lambda = \begin{bmatrix}
\lambda_1 & 0 & \cdots & 0 \\
\\
0 & \lambda_2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n
\end{bmatrix}
\),
where, each diagonal element is an eigen value corresponding to an eigen vector \(\mathbf{v}_i\).
Let’s recall the characteristic equation of a matrix for calculating eigen values:
\(\mathbf{A} \mathbf{v} = \lambda \mathbf{v}\)
Let’s use the consolidated matrix for eigen values and eigen vectors described above:
i.e, \(\mathbf{A} \mathbf{V} = \mathbf{\Lambda} \mathbf{V}\)
For diagonalisation:
=> \(\mathbf{\Lambda} = \mathbf{V}^{-1} \mathbf{A} \mathbf{V}\)
We can see that, using the above equation, we can represent the matrix \(\mathbf{A}\) as a
diagonal matrix \(\mathbf{\Lambda}\) using the matrix of eigen vectors \(\mathbf{V}\).
Just reshuffling the above equation will give us the Eigen Value Decomposition of the matrix \(\mathbf{A}\):
\(\mathbf{A} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^{-1}\)
Important: Given that \(\mathbf{V}^{-1}\) exists, i.e, all the eigen vectors are linearly independent.
=> \( \mathbf{V} = \begin{bmatrix}
1 & 1 \\
\\
1 & -1 \\
\end{bmatrix}
\),
\(\quad \mathbf{\Lambda} = \begin{bmatrix}
3 & 0 \\
\\
0 & 1
\end{bmatrix}
\)
\( \because \mathbf{A} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^{-1}\)
We know, \( \mathbf{V} ~and~ \mathbf{\Lambda} \), we need to calculate \(\mathbf{V}^{-1}\).
\(\mathbf{V}^{-1} = \frac{1}{2}\begin{bmatrix} 1 & 1 \\ \\ 1 & -1 \\ \end{bmatrix} \)
\( \therefore \mathbf{V} \mathbf{\Lambda} \mathbf{V}^{-1} = \begin{bmatrix}
1 & 1 \\
\\
1 & -1 \\
\end{bmatrix} \begin{bmatrix}
3 & 0 \\
\\
0 & 1
\end{bmatrix} \frac{1}{2}\begin{bmatrix}
1 & 1 \\
\\
1 & -1 \\
\end{bmatrix}
\)
\( = \frac{1}{2}
\begin{bmatrix}
3 & 1 \\
\\
3 & -1 \\
\end{bmatrix} \begin{bmatrix}
1 & 1 \\
\\
1 & -1 \\
\end{bmatrix} = \frac{1}{2}\begin{bmatrix}
4 & 2 \\
\\
2 & 4 \\
\end{bmatrix}
\)
\( = \begin{bmatrix}
2 & 1 \\
\\
1 & 2
\end{bmatrix} = \mathbf{A}
\)
Spectral decomposition is a specific type of eigendecomposition that applies to a symmetric matrix,
requiring its eigenvectors to be orthogonal.
In contrast, a general eigendecomposition applies to any diagonalizable matrix and does not require the eigenvectors
to be orthogonal.
The eigen vectors corresponding to distinct eigen values are orthogonal.
However, the matrix \(\mathbf{V}\) formed by the eigen vectors as columns is NOT orthogonal,
because the rows/columns are NOT orthonormal i.e unit length.
So, in order to make the matrix \(\mathbf{V}\) orthogonal, we need to normalize the rows/columns of the matrix
\(\mathbf{V}\), i.e, make, each eigen vector(column) unit length, by dividing the vector by its magnitude.
After normalisation we get orthogonal matrix \(\mathbf{Q}\) that is composed of unit length and orthogonal eigen vectors
or orthonormal eigen vectors.
Since, matrix \(\mathbf{Q}\) is orthogonal, => \(\mathbf{Q}^T = \mathbf{Q}^{-1}\)
The eigen value decomposition of a square matrix is:
\(\mathbf{A} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^{-1}\)
And, the spectral decomposition of a real symmetric matrix is:
\(\mathbf{A} = \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^T\)
Important: Note that, we are discussing only the special case of real symmetric matrix here,
because a real symmetric matrix is guaranteed to have all real eigenvalues.
End of Section

Principal Component Analysis (PCA)
It is a dimensionality reduction technique that finds the direction of maximum variance in the data.
Note: Some loss of information will always be there in dimensionality reduction, because there will be some variability
in data along the direction that is dropped, and that will be lost.
Goal:
Fundamental goal of PCA is to find the new set of orthogonal axes, called the principal components, onto which
the data can be projected, such that, the variance of the projected data is maximum.
Say, we have data, \(D:X \in \mathbb{R}^{n \times d}\),
n is the number of samples
d is the number of features or dimensions of each data point.
In order to find the directions of maximum variance in data, we will use the covariance matrix of data.
Covariance matrix (C) summarizes the spread and relationship of the data in the original d-dimensional space.
\(C_{d \times d} = \frac{1}{n-1}X^TX \), where \(X\) is the data matrix.
Note: (n-1) in the denominator is for unbiased estimation(Bessel’s correction) of covariance matrix.
\(C_{ii}\) is the variance of the \(i^{th}\) feature.
\(C_{ij}\) is the co-variance between feature \(i\) and feature \(j\).
Trace(C) = Sum of diagonal elements of C = Total variance of data.
Algorithm:
Data is first mean centered, i.e, make mean = 0, i.e, subtract mean from each data point.
\(X = X - \mu\)
Compute the covariance matrix with mean centered data.
\(C = \frac{1}{n-1}X^TX \),
\( \quad
\Sigma =
\begin{bmatrix}
var(f_1) & cov(f_1f_2) & \cdots & cov(f_1f_d) \\
cov(f_2f_1) & var(f_2) & \cdots & cov(f_2f_d) \\
\vdots & \vdots & \ddots & \vdots \\
cov(f_df_1) & cov(f_df_2) & \cdots & var(f_d)
\end{bmatrix}
_{\text{d x d}}
\)
Perform the eigen value decomposition of covariance matrix.
\( C = Q \Lambda Q^T \)
\(C\): Orthogonal matrix of eigen vectors of covariance matrix.
New rotated axes or prinicipal components of the data.
\(\Lambda\): Diagonal matrix of eigen values of covariance matrix.
Scaling of variance along new eigen basis.
Note: Eigen values are sorted in descending order, i.e \( \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_d \).
Project the data onto the new axes or principal components/directions.
Note: k < d = reduced dimensionality.
\(X_{new} = Z = XQ_k\)
\(X_{new}\): Projected data or principal component score
Variance of projected data is given by the eigen value of the co-variance matrix.
Covariance of projected data = \((XQ)^TXQ \)
Therefore, the diagonal matrix \( \Lambda \) captures the variance along every principal component direction.
End of SectionSingular Value Decomposition (SVD):
It decomposes any matrix into a rotation, a scaling (based on singular values), and another rotation.
It is a generalization of the eigen value decomposition(for square matrix) to rectangular matrices.
Any rectangular matrix can be decomposed into a product of three matrices using SVD, as follows:
\(\mathbf{U}\): Set of orthonormal eigen vectors of \(\mathbf{AA^T}_{m \times m} \)
\(\mathbf{V}\): Set of orthonormal eigen vectors of \(\mathbf{A^TA}_{n \times n} \)
\(\mathbf{\Sigma}\): Rectangular diagonal matrix, whose diagonal values are called singular values;
square root of non-zero eigen values of \(\mathbf{AA^T}\).
Note: The number of non-zero diagonal entries in \(\mathbf{\Sigma}\) = rank of matrix \(\mathbf{A}\).
Rank (r): Number of linearly independent rows or columns of a matrix.
\( \Sigma = \begin{bmatrix}
\sigma_{11} & 0 & \cdots & 0 \\
\\
0 & \sigma_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
\cdots & \cdots & \sigma_{rr} & \vdots \\
0 & 0 & \cdots & 0
\end{bmatrix}
\),
such that, \(\sigma_{11} \geq \sigma_{22} \geq \cdots \geq \sigma_{rr}\), r = rank of \(\mathbf{A}\).
Singular value decomposition, thus refers to the set of scale factors \(\mathbf{\Sigma}\) that are fundamentally
linked to the matrix’s singularity and rank.
Note: If rank of matrix < dimensions, then 1 or more of the singular values are zero, i.e, dimension collapse.
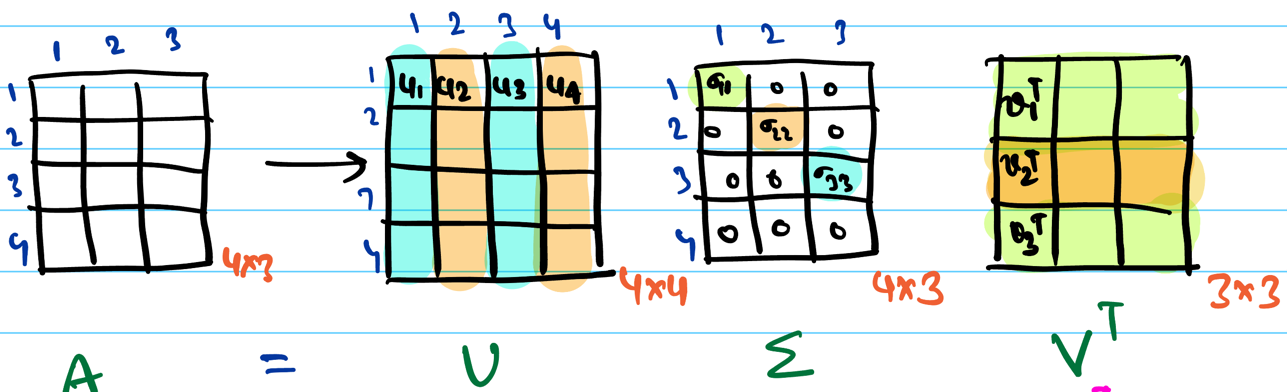
We can perform singular value decomposition on the image matrix and find the minimum number of top ranks required to
to successfully reconstruct the original image back.
Say we performed the SVD on the image matrix and found that top 20 rank singular values, out of 1000, are sufficient to
tell what the picture is about.
\(\mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T \)
\( = u_1 \sigma_1 v_1^T + u_2 \sigma_2 v_2^T + \cdots + u_r \sigma_r v_r^T \), where \(r = 20\)
A = sum of ‘r=20’ matrices of rank=1.
Now, we need to send only the \(u_i, \sigma_i , v_i\) values for i=20, i.e, top 20 ranks to earth
and then do the calculation to reconstruct the approximation of original image.
\(\mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_{1000} \end{bmatrix}\)
\(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_{1000} \end{bmatrix}\)
So, we need to send data corresponding to 20 (rank=1) matrices, i.e, \(u_i, v_i ~and~ \sigma_i\) = (1000 + 1000 + 1)20 = 200020 pixels (approx)
Therefore, compression rate = (2000*20)/(10^6) = 1/25
Low Rank Approximation:
The process of approximating any matrix by a matrix of a lower rank, using singular value decomposition.
It is used for data compression.
Any matrix A of rank ‘r’ can be written as sum of rank=1 outer products:
\[ \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T = \sum_{i=1}^{r} \sigma_i \mathbf{u}_i \mathbf{v}_i^T \]\( \mathbf{u}_i : i^{th}\) column vector of \(\mathbf{U}\)
\( \mathbf{v}_i^T : i^{th}\) column vector of \(\mathbf{V}^T\)
\( \sigma_i : i^{th}\) singular value, i.e, diagonal entry of \(\mathbf{\Sigma}\)
Since, the singular values are arranged from largest to smallest, i.e, \(\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r\),
The top ranks capture the vast majority of the information or variance in the matrix.
So, in order to get the best rank-k approximation of the matrix,
we simply truncate the summation after the k’th term.
The approximation \(\mathbf{A_k}\) is called the low rank approximation of \(\mathbf{A}\),
which is achieved by keeping only the largest singular values and corresponding vectors.
Applications:
End of SectionLet \(\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}_{\text{n×1}}\) be a vector, i.e, \(\mathbf{x} \in \mathbb{R}^n\).
Let \(f(x)\) be a function that maps a vector to a scalar, i.e, \(f : \mathbb{R}^n \rightarrow \mathbb{R}\).
The derivative of function \(f(x)\) with respect to \(\mathbf{x}\) is defined as:
Assumption: All the first order partial derivatives exist.
e.g.:
Let’s calculate \(\frac{\partial y}{\partial x_k}\), i.e, for the \(k^{th}\) element and sum it over 1 to n.
The \(k^{th}\) element \(x_k\) will appear 2 times in the below summation, i.e, when \(i=k ~and~ j=k\)
Above, we saw the gradient of a scalar valued function, i.e, a function that maps a vector to a scalar, i.e,
\(f : \mathbb{R}^n \rightarrow \mathbb{R}\).
There is another kind of function called vector valued function, i.e, a function that maps a vector to another vector, i.e,
\(f : \mathbb{R}^n \rightarrow \mathbb{R}^m\).
The Jacobian is the matrix of all first-order partial derivatives of a vector-valued function,
while the gradient is a vector representing the partial derivatives of a scalar-valued function.
Note: Gradient is a special case of the Jacobian;
it is the transpose of the Jacobian for a scalar valued function.
Let, \(f(x)\) be a function that maps a vector to another vector, i.e, \(f : \mathbb{R}^n \rightarrow \mathbb{R}^m\)
\(f(x)_{m \times 1} = \mathbf{A_{m \times n}x_{n \times 1}}\), where,
\(\quad
\mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix}
_{\text{m x n}}
\),
\(\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}_{\text{n x 1}}\),
\(f(x) = \begin{bmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_m(x) \end{bmatrix}_{\text{m x 1}}\)
The above matrix is called Jacobian matrix of \(f(x)\).
Assumption: All the first order partial derivatives exist.
Hessian Matrix:
It is a square matrix of second-order partial derivatives of a scalar-valued function.
This is used to characterize the curvature of a function at a give point.
Let, \(f(x)\) be a function that maps a vector to a scalar value, i.e, \(f : \mathbb{R}^n \rightarrow \mathbb{R}\)
The Hessian matrix is defined as:
Note: Most functions in Machine Learning where second-order partial derivatives are continuous, the Hessian is symmetrix.
\( H_{i,j} = H_{j,i} = \frac{\partial f^2(x)}{\partial x_i \partial x_j } = \frac{\partial f^2(x)}{\partial x_j \partial x_i } \)
e.g:
\(f(x) = \mathbf{x^TAx}\), where, A is a symmetric matrix, and f(x) is a scalar valued function.
\(Gradient = \frac{\partial }{\partial x}(\mathbf{x^TAx}) = 2\mathbf{Ax}\), since A is symmetric.
\(Hessian = \frac{\partial^2 }{\partial x^2}(\mathbf{x^TAx}) = \frac{\partial }{\partial x}2\mathbf{Ax} = 2\mathbf{A}\)
\(f(x,y) = x^2 + y^2\)
\(Gradient = \nabla f = \begin{bmatrix} \frac{\partial f}{\partial x}\\ \\ \frac{\partial f}{\partial x} \end{bmatrix}
= \begin{bmatrix} 2x+0 \\ \\ 0+2y \end{bmatrix} = \begin{bmatrix} 2x \\ \\ 2y \end{bmatrix}\)
\(Hessian = \nabla^2 f = \begin{bmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y}\\
\\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} \end{bmatrix}
= \begin{bmatrix} 2 & 0 \\ \\ 0 & 2 \end{bmatrix}\)
Let, A is a mxn matrix, i.e \(A \in \mathbb{R}^{m \times n}\)
\(\mathbf{A} =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix}
_{\text{m x n}}
\)
Let f(A) be a function that maps a matrix to a scalar value, i.e, \(f : \mathbb{R}^{m \times n} \rightarrow \mathbb{R}\)
, then derivative of function f(A) w.r.t A is defined as:
e.g.:
End of SectionVector Norm:
It is a measure of the size of a vector or distance from the origin.
Vector norm is a function that maps a vector to a real number, i.e, \({\| \cdot \|} : \mathbb{R}^n \rightarrow \mathbb{R}\).
Vector Norm should satisfy following 3 properties:
P-Norm:
It is a generalised form of most common family of vector norms, also called Minkowski norm.
It is defined as:
We can change the value of \(p\) to get different norms.
L1 Norm:
It is the sum of absolute values of all the elements of a vector; also known as Manhattan distance.
p=1:
L2 Norm:
It is the square root of the sum of squares of all the elements of a vector; also known as Euclidean distance.
p=2:
L-\(\infty\) Norm:
It is the maximum of absolute values of all the elements of a vector; also known as Chebyshev distance.
p=\(\infty\):
Matrix Norm:
It is a function that assigns non-negative size or magnitude to a matrix.
Matrix Norm is a function that maps a matrix to a non-negative real number, i.e, \({\| \cdot \|} : \mathbb{R}^{m \times n} \rightarrow \mathbb{R}\)
It should satisfy following 3 properties:
There are 2 types of matrix norms:
Frobenius Norm:
It is equivalent to the Euclidean norm of the matrix if it were flattened into a single vector.
If A is a matrix of size \(m \times n\), then, Frobenius norm is defined as:
\(\sigma_i\) is the \(i\)th singular value of matrix A.
Vector Induced Norm:
It measures the maximum stretching a matrix can apply when multiplied with a vector,
where the vector has a unit length under the chosen vector norm.
Matrix Induced by Vector P-Norm:
P-Norm:
P=1 Norm:
P=\(\infty\) Norm:
P=2 Norm:
Also called Spectral norm, i.e, maximum factor by which the matrix can stretch a unit vector in Euclidean norm.
For example:
Let, matrix \(\mathbf{A} = \begin{bmatrix} a_{11} & a_{12} \\ \\ a_{21} & a_{22} \end{bmatrix}\), then find Frobenius norm.
\({\| A \|_F} = \sqrt{a_{11}^2 + a_{12}^2 + a_{21}^2 + a_{22}^2}\)
\(\mathbf{A}^T = \begin{bmatrix} a_{11} & a_{22} \\ \\ a_{12} & a_{22} \end{bmatrix}\)
=> \(\mathbf{A^TA} =
\begin{bmatrix} a_{11} & a_{22} \\ \\ a_{12} & a_{22} \end{bmatrix}
\begin{bmatrix} a_{11} & a_{12} \\ \\ a_{21} & a_{22} \end{bmatrix}
= \begin{bmatrix} a_{11}^2 + a_{12}^2 & a_{11}.a_{21} + a_{12}.a_{22} \\ \\ a_{21}.a_{11} + a_{22}.a_{12} & a_{21}^2 + a_{22}^2 \end{bmatrix}
\)
Therefore, \(Trace(\mathbf{A^TA}) = a_{11}^2 + a_{12}^2 + a_{21}^2 + a_{22}^2\)
=> \({\| A \|_F} = \sqrt{Trace(A^TA)} = \sqrt{a_{11}^2 + a_{12}^2 + a_{21}^2 + a_{22}^2}\)
Let, matrix \(\mathbf{A} = \begin{bmatrix} 1 & -2 & 3 \\ \\ 4 & 5 & -6 \end{bmatrix}\), then
Column 1 absolute value sum = |1|+|4| = 5
Column 2 absolute value sum = |-2|+|5|= 7
Column 3 absolute value sum = |3|+|-6|= 9
Row 1 absolute value sum = |1|+|-2|+|3| = 6
Row 2 absolute value sum = |4|+|5|+|-6| = 15
\({\| A \|_1} = max(5,7,9) = 9\) = max column absolute value sum.
\({\| A \|_\infty} = max(6,15) = 15\) = max row absolute value sum.
\(\mathbf{A} = \mathbf{U \Sigma V^T} \) , where
\(\mathbf{U} = \mathbf{AA^T} \),
\(\mathbf{V} = \mathbf{A^TA} \)
Let’s find the largest eigen value of \(\mathbf{A^TA} \), square root of which will give the largest singular value of \(\mathbf{A}\).
\( \mathbf{V} = \mathbf{A^TA} =
\begin{bmatrix} 2 & 1 \\ \\ 1 & 2 \end{bmatrix}
\begin{bmatrix} 2 & 1 \\ \\ 1 & 2 \end{bmatrix}
= \begin{bmatrix} 5 & 4 \\ \\ 4 & 5 \end{bmatrix}
\)
Now, lets find the eigen values of the above matrix V:
\(det(V-\lambda I) = 0 \)
=> \(
det\begin{bmatrix} 5 - \lambda & 4 \\ \\ 4 & 5- \lambda \end{bmatrix} = 0
\)
=> \( (5 - \lambda)^2 - 16 = 0 \)
=> \( (5 - \lambda) = \pm 4 \)
=> \( (5 - \lambda) = 4 \) or \( (5 - \lambda) = -4 \)
=> \( \lambda = 1 \) or \( \lambda = 9 \)
=> Largest Singular Value = Square root of largest eigen value = \(\sqrt{9} = 3\)
Therefore, \({\| A \|_2} = \sigma_{max}(A) = 3\)
End of Section
Equation of a line is of the form \(y = mx + c\).
To represent a line in 2D space, we need 2 things:
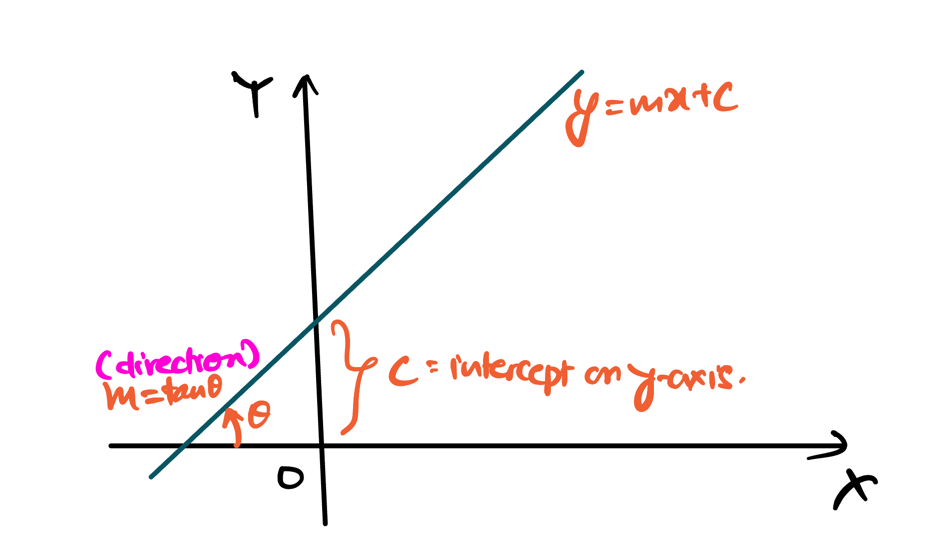
Similarly, to represent a hyperplane in d-dimensions, we need 2 things:
Note: There can be only 2 directions of the hyperplane, i.e, direction of a unit vector perpendicular to the hyperplane:
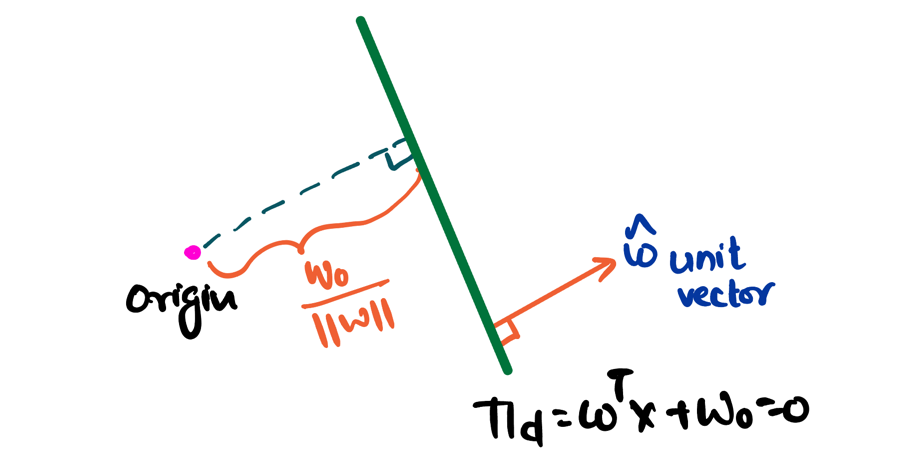
If a point ‘x’ is on the hyperplane, then it satisfies the below equation:
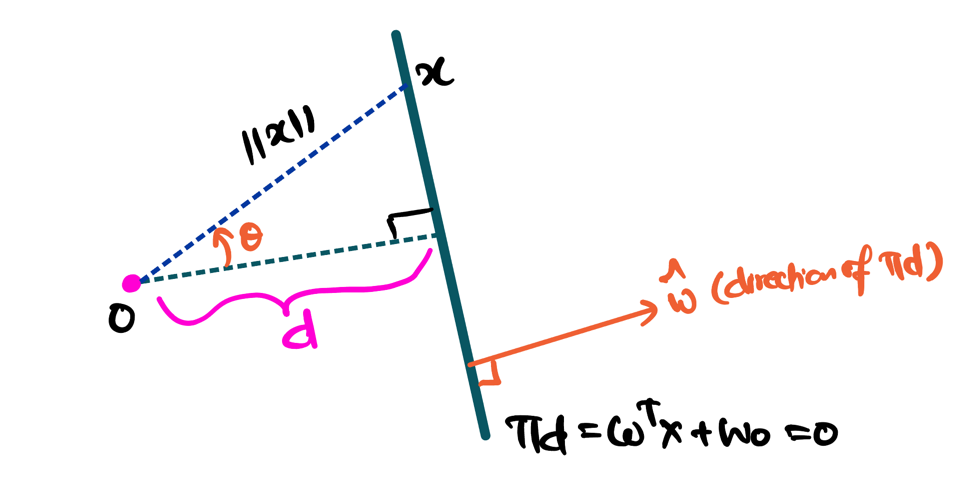
Key Points:
Equation of a hyperplane is: \(\pi_d = \mathbf{w}^\top \mathbf{x} + w_0 = 0\)
Let, the equation of the line/hyperplane in 2D be:
\(\pi_d = 1.x + 0.y + w_0 = x + w_0 = 0\)
Case 1: \(w_0 < 0\), say \(w_0 = -5\)
Therefore, equation of hyperplane: \( x - 5 = 0 => x = 5\)
Here, the hyperplane(line) is located in the same direction as the unit vector w.r.t the origin,
i.e, towards the +ve x-axis direction.
Case 2: \(w_0 > 0\), say \(w_0 = 5\)
Therefore, equation of hyperplane: \( x + 5 = 0 => x = -5\)
Here, the hyperplane(line) is located in the opposite direction as the unit vector w.r.t the origin,
i.e, towards the -ve x-axis direction.
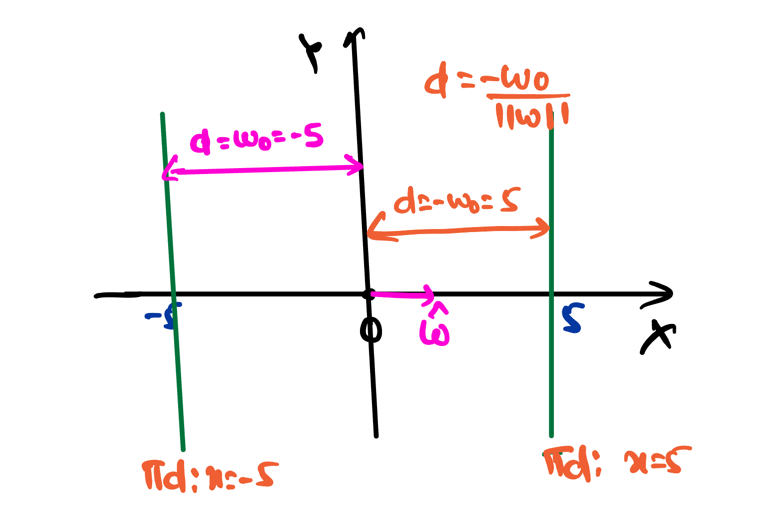
A hyperplane divides a space into 2 distinct parts called half-spaces.
e.g.: A 2D hyperplane divided a 3D space into 2 distinct parts.
Similar example in real world: A wall divides a room into 2 distinct spaces.
Positive Half-Space:
A half space that is in the same direction as the unit vector w.r.t the origin.
Negative Half-Space:
A half space that is in the opposite direction as the unit vector w.r.t the origin.
from equations (1) & (2), we can say that:
\[ \Vert \mathbf{w} \Vert \Vert \mathbf{x_1} \Vert cos{\theta} + w_0 < \Vert \mathbf{w} \Vert \Vert \mathbf{x_1\prime} \Vert cos{\theta} + w_0 \]Everything is same on both the sides except \(\Vert \mathbf{x_1}\Vert\) and \(\Vert \mathbf{x_1\prime\Vert}\), so:
\[ \mathbf{w}^\top \mathbf{x_1} + w_0 < 0 \]i.e, negative half-space, opposite to the direction of unit vector or towards the origin.
Similarly,
i.e, positive half-space, same as the direction of unit vector or away from the origin.
Equation of distance of any point \(x\prime\) from the hyperplane:
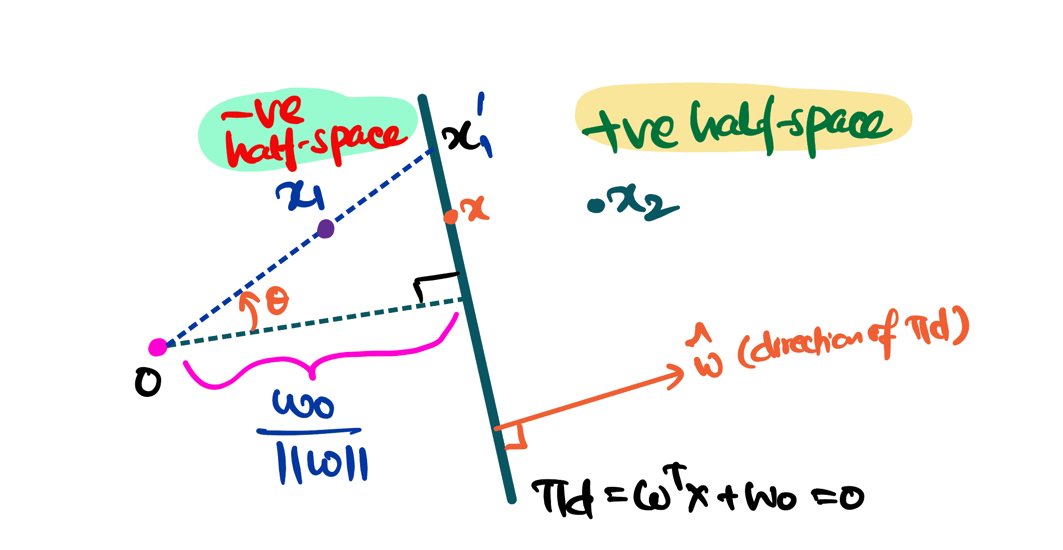
The above concept of equation of hyperplane will be very helpful when we discuss the following topics later:
End of SectionThis sheet contains all the topics that will be covered for Calculus for AI & ML.
Integration is a mathematical tool that is used to find the area under a curve.
Let’s understand integration with the help of few simple examples for finding area under a curve:
Area of a triangle: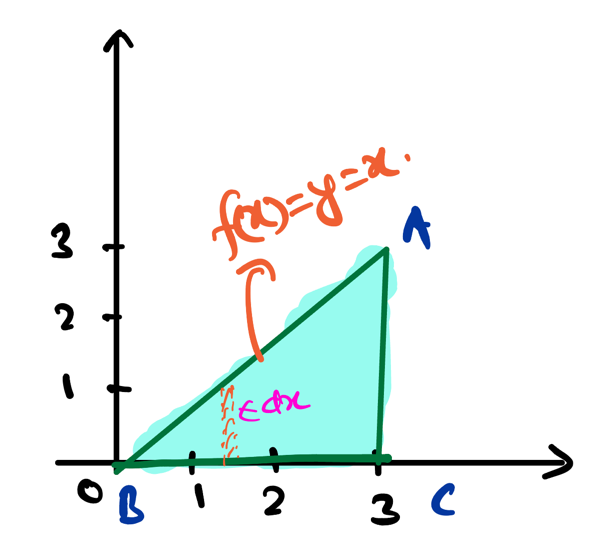
Area of a rectangle: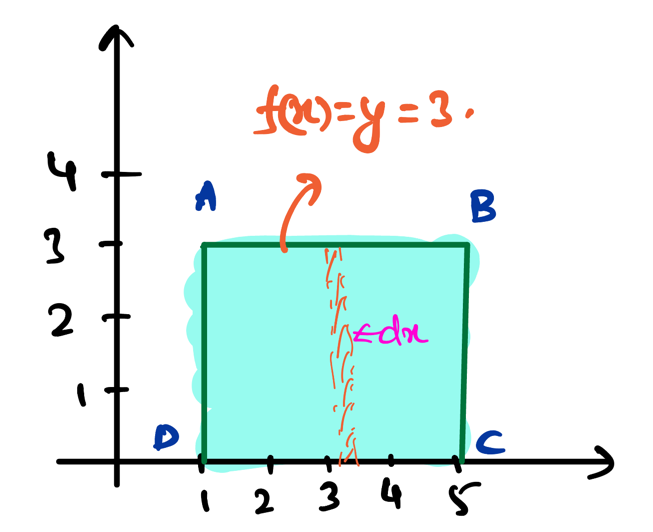
Note: The above examples were standard straight forward, where we know a direct formula for finding area under a curve.
But, what if we have such a shape, for which, we do NOT know a ready-made formula, then how do we calculate
the area under the curve.
Let’s see an example:
3. Area of a part of parabola: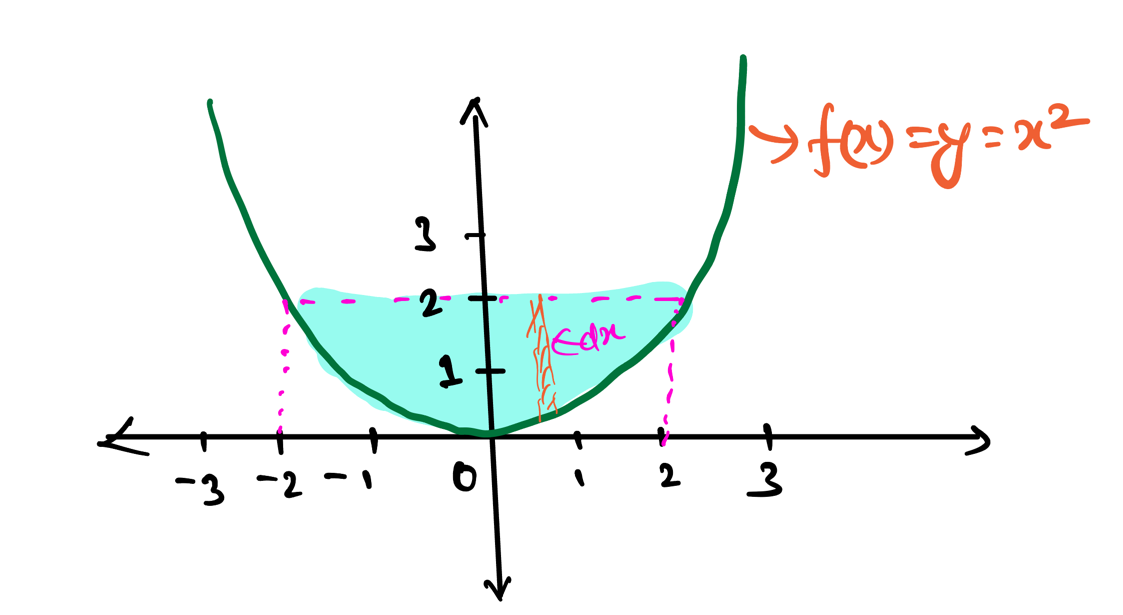
Differentiation is a mathematical tool that is used to find the derivative or rate of change of a function
at a specific point.
Note: For a line, the slope is constant, but for a parabola, the slope is changing at every point.
How do we calculate the slope at a given point?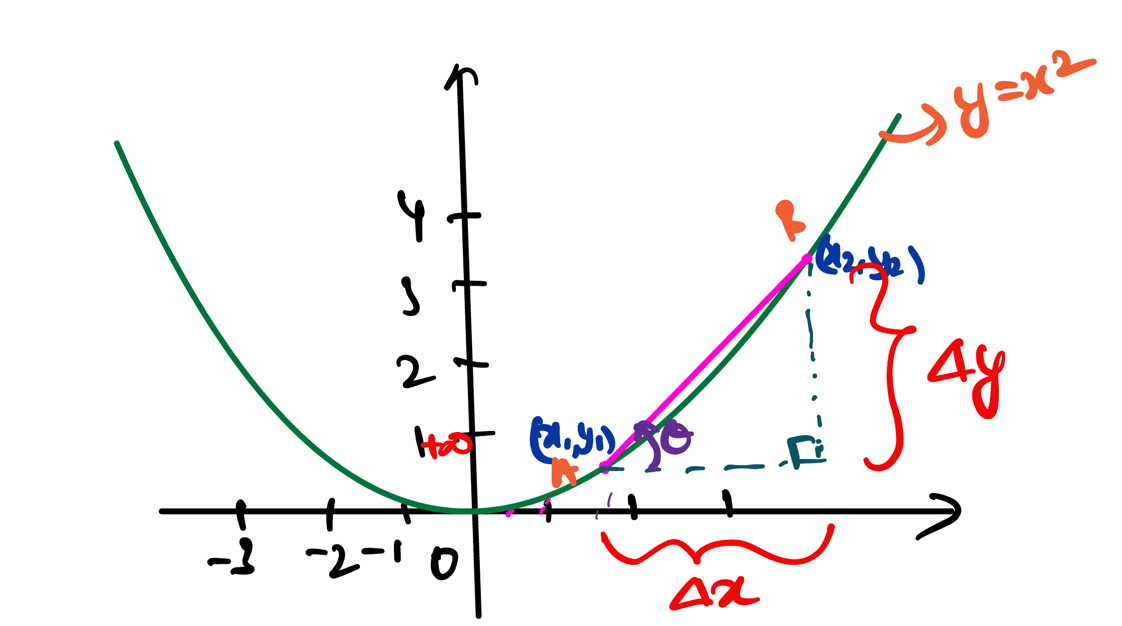
Let AB is a secant on the parabola, i.e, line connecting any 2 points on the curve.
Slope of secant = \(tan\theta = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}\)
As \(\Delta x \rightarrow 0\), secant will become a tangent to the curve, i.e, the line will touch the curve only
at 1 point.
\(dx = \Delta x \rightarrow 0\)
\(x_2 = x_1 + \Delta x \)
\(y_2 = f(x_2) = f(x_1 + \Delta x) \)
Slope at \(x_1\) =
e.g.:
\( y = f(x) = x^2\), find the derivative of f(x) w.r.t x.
We will understand few important rules of differentiation that are most frequently used in Machine Learning.
Sum Rule:
Product Rule:
e.g.:
\( h(x) = x^2 sin(x) \), find the derivative of h(x) w.r.t x.
Let, \(f(x) = x^2 , g(x) = sin(x)\).
Quotient Rule:
e.g.:
\( h(x) = sin(x)/x \), find the derivative of h(x) w.r.t x.
Let, \(f(x) = sin(x) , g(x) = x\).
Chain Rule:
e.g.:
\( h(x) = log(x^2) \), find the derivative of h(x) w.r.t x.
Let, \( u = x^2 \)
Now, let’s dive deeper and understand the concepts that required for differentiation, such as, limits, continuity, differentiability, etc.
Limit of a function f(x) at any point ‘c’ is the value that f(x) approaches, as x gets very close to ‘c’,
but NOT necessarily equal to ‘c’.
One-sided limit: value of the function, as it approaches a point ‘c’ from only one direction, either left or right.
Two-sided limit: value of the function, as it approaches a point ‘c’ from both directions, left and right, simultaneously.
e.g.:
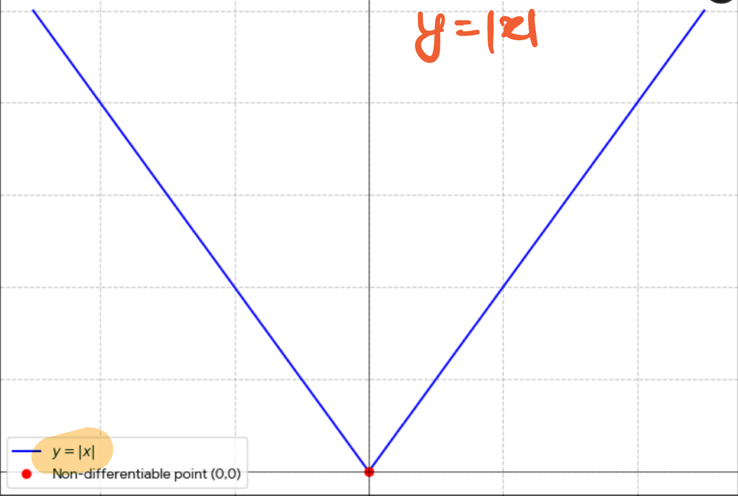
A function f(x) is said to be continuous at a point ‘c’, if its graph can be drawn through that point,
without lifting the pen.
Continuity bridges the gap between the function’s value at the given point and the limit.
Conditions for Continuity:
A function f(x) is continuous at a point ‘c’, if and only if, all the below 3 conditions are met:
e.g.:


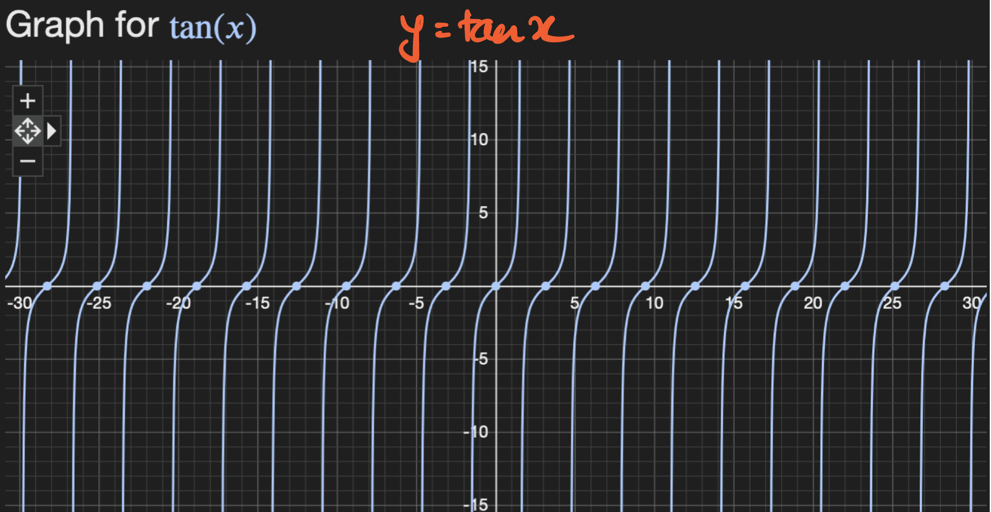
A function is differentiable at a point ‘c’, if derivative of the function exists at that point.
A function must be continuous at the given point ‘c’ to be differentiable at that point.
Note: A function can be continuous at a given point, but NOT differentiable at that point.
e.g.:
We know that \( f(x) = |x| \) is continuous at x=0, but its NOT differentiable at x=0.
Critical Point:
A point of the function where the derivative is either zero or undefined.
These critical points are candidates for local maxima or minima,
which are the highest and lowest points in a function’s immediate neighborhood, respectively.
Maxima:
Highest point w.r.t immediate neighbourhood.
f’(x)/gradient/slope changes from +ve to 0 to -ve, therefore, change in f’(x) is -ve.
=> f’’(x) < 0
Let, \(f(x) = -x^2; \quad f'(x) = -2x; \quad f''(x) = -2 < 0 => maxima\)
| x | f’(x) |
|---|---|
| -1 | 2 |
| 0 | 0 |
| 1 | -2 |
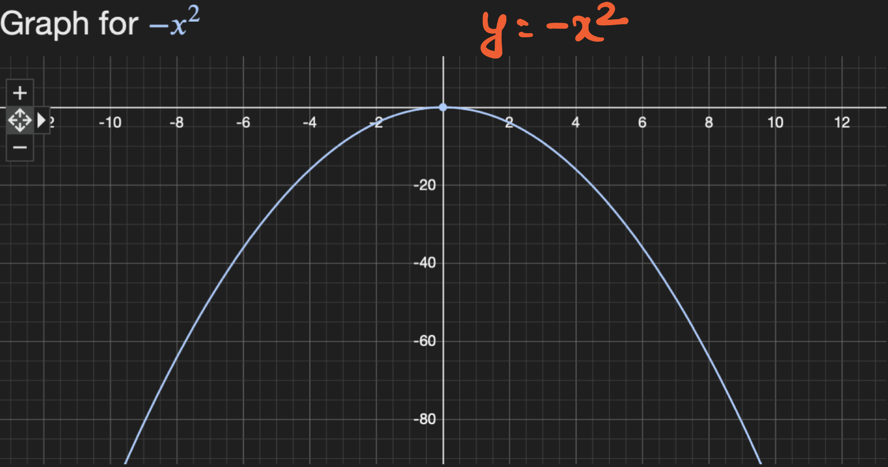
Minima:
Lowest point w.r.t immediate neighbourhood.
f’(x)/gradient/slope changes from -ve to 0 to +ve, therefore, change in f’(x) is +ve.
=> f’’(x) > 0
Let, \(f(x) = x^2; \quad f'(x) = 2x; \quad f''(x) = 2 > 0 => minima\)
| x | f’(x) |
|---|---|
| -1 | -2 |
| 0 | 0 |
| 1 | 2 |

e.g.:
Let \(f(x) = 2x^3 + 5x^2 + 3 \), find the maxima and minima of f(x).
To find the maxima and minima, lets take the derivative of the function and equate it to zero.
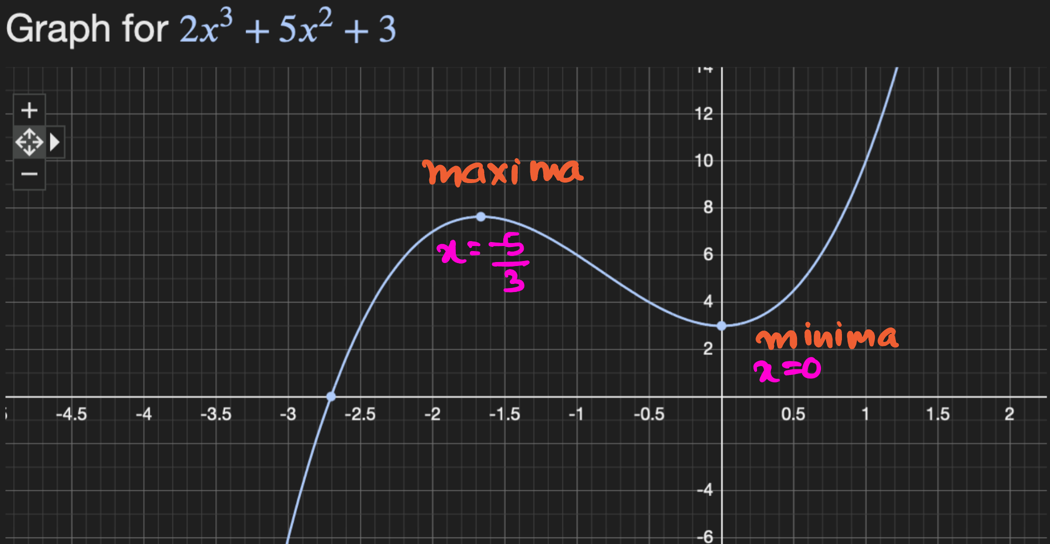
\(f(x,y) = z = x^2 + y^2\), find the minima of f(x,y).
Since, this is a multi-variable function, we will use vector and matrix for calculation.
Partial Derivative:
Partial derivative \( \frac{\partial f(x,y)}{\partial x} ~or~ \frac{\partial f(x,y)}{\partial y} \)is the rate of change
or derivative of a multi-variable function w.r.t one of its variables,
while all the other variables are held constant.
Let’s continue solving the above problem, and calculate the Hessian, i.e, 2nd order derivative of f(x,y):
Since, determinant of Hessian = 4 > 0 and \( \frac{\partial^2 f_z}{\partial x^2} > 0\) => (x=0, y=0) is a point of minima.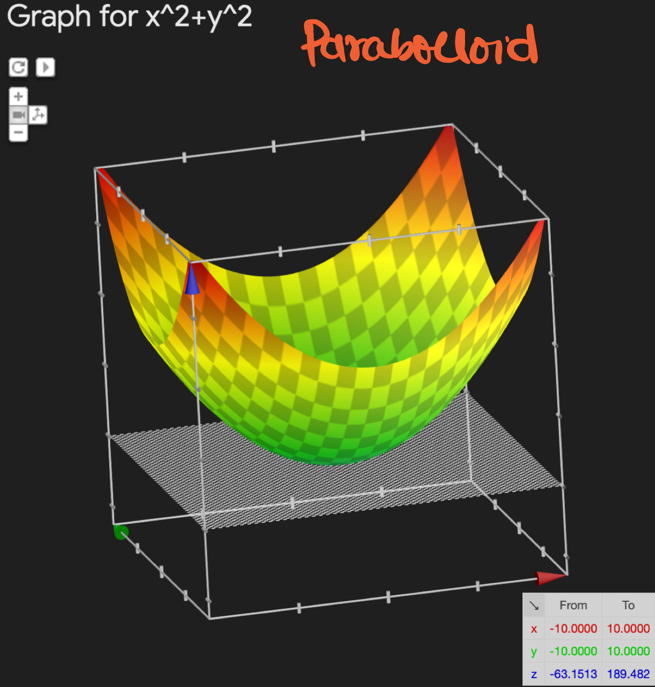
Hessian Interpretation:
Saddle Point is a critical point where the function is maximum w.r.t one variable,
and minimum w.r.t to another.
e.g.:
Let, \(f(x,y) = z = x^2 - y^2\), find the point of optima for f(x,y).
Since, determinant of Hessian = -4 < 0 => (x=0, y=0) is a saddle point.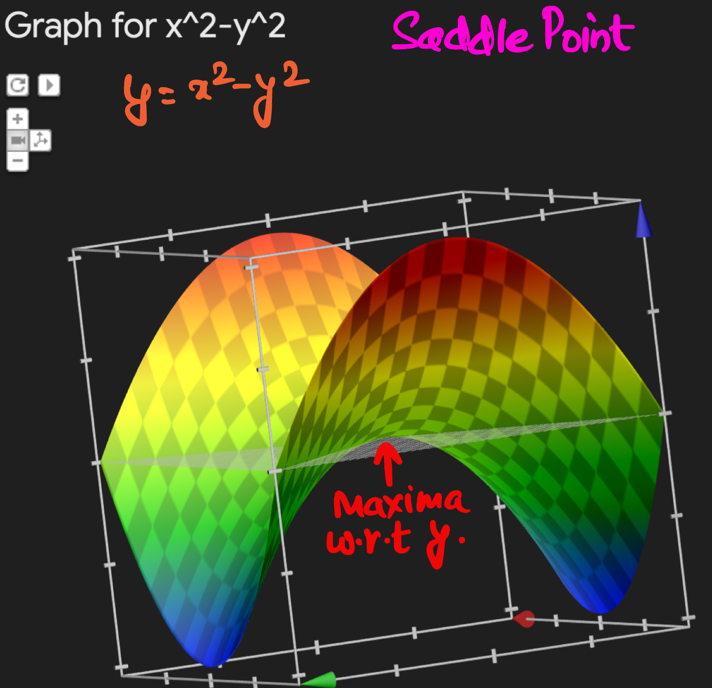
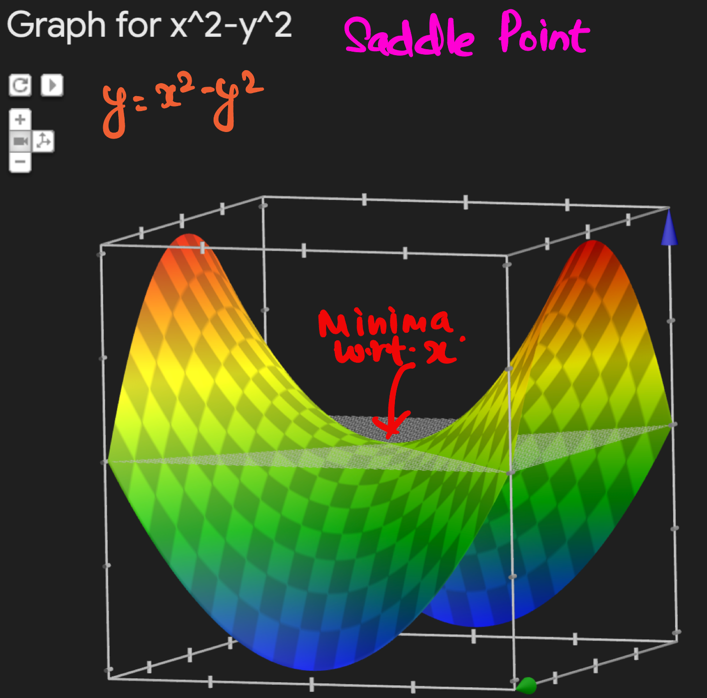
End of Section
Loss Function:
It quantifies error of a single data point in a dataset.
e.g.: Squared Loss, Hinge Loss, Absolute Loss, etc, for a single data point.
Cost Function:
It is the average of all losses over the entire dataset.
e.g.: Mean Squared Error(MSE), Mean Absolute Error(MAE), etc.
Objective Function:
It is the over-arching objective of an optimization problem, representing the function that is minimized or maximized.
e.g.: Minimize MSE.
Let’s understant this through an example:
Task:
Predict the price of a company’s stock based on its historical data.
Objective Function:
Minimize the difference between actual and predicted price.
Let, \(y\): original or actual price
\(\hat y\): predicted price
Say, the dataset has ’n’ such data points.
Loss Function:
loss = \( y - \hat y \) for a single data point.
We want to minimize the loss for all ’n’ data points.
Cost Function:
We want to minimize the average/total loss over all ’n’ data points.
So, what are the ways ?
Key Points:
Convexity:
It refers to a property of a function where a line segment connecting any two points on its graph
lies above or on the graph itself.
A convex function is curved upwards.
It is always described by a convex set.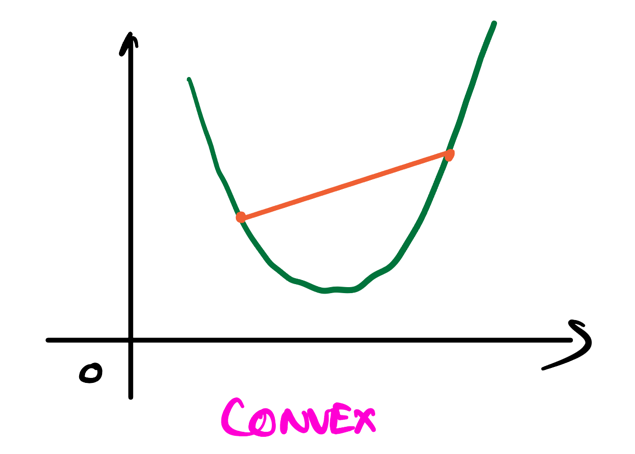
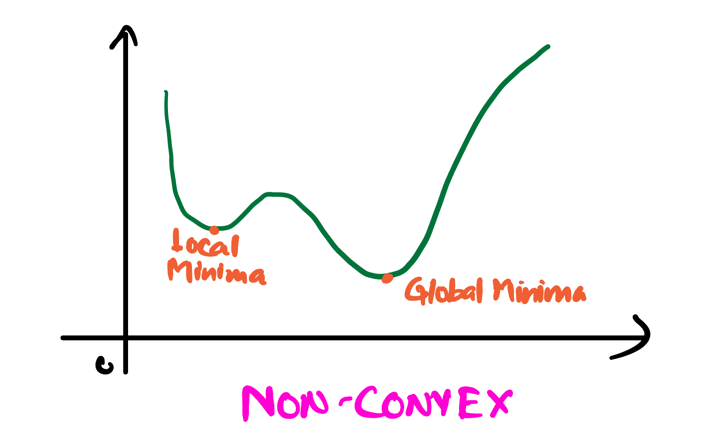
Convex Set:
A convex set is a set of points in which the straight line segment connecting any two points in the set lies
entirely within that set.
A set \(C\) is convex if for any two points \(x\) and \(y\) in \(C\), the convex combination
\(\theta x+(1-\theta )y\) is also in \(C\) for all values of \(\theta \) where \(0\le \theta \le 1\).
A function \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) is convex if for all values of \(x,y\) and \(0\le \theta \le 1\),
\[ f(\theta x + (1-\theta )y) \le \theta f(x) + (1-\theta )f(y) \]Second-Order Test:
If a function is twice differentiable, i.e, 2nd derivative exists, then the function is convex,
if and only if, the Hessian is positive semi-definite for all points in its domain.
Positive Definite:
A symmetric matrix is positive definite if and only if:
Note: If the Hessian is positive definite, then the function is convex; has upward curvature in all directions.
Positive Semi-Definite:
A symmetric matrix is positive semi-definite if and only if:
Note: If the Hessian is positive definite, then the function is not strictly convex, but flat in some directions.
All machine learning algorithms minimize loss (mostly), so we need to find the optimum parameters for the model that
minimizes the loss.
This is an optimization problem, i.e, find the best solution from a set of alternatives.
Note: Convexity ensures that there is only 1 minima for the loss function.
Optimization:
It is the iterative procedure of finding the optimum parameter \(x^*\) that minimizes the loss function f(x).
Let’s formulate an optimization problem for a model to minimize the MSE loss function discussed above:
Note: To minimize the loss, we want \(y_i, \hat y_i\) to be as close as possible,
for that we want to find the optimum weights \(w, w_0\) of the model.
Important:
Deep Learning models have non-convex loss function, so it is challenging to reach the global minima,
so any local minima is also a good enough solution.
Read more about Maxima-Minima
Constrained Optimization:
It is an optimization process to find the best possible solution (min or max), but within a set of limitations or
restrictions called constraints.
Constraints limit the range of acceptable values; they can be equality constraints or inequality constraints.
e.g.:
Minimize f(x) subject to following constraints:
Equality Constraints: \( g_i(x) = c_i \forall ~i \in \{1,2,3, \ldots, n\} \)
Inequality Constraints: \( h_j(x) \le d_j \forall ~j \in \{1,2,3, \ldots, m\}\)
Lagrangian Method:
Lagrangian method converts a constrained optimization problem to an unconstrained optimization problem,
by introducing a new variable called Lagrange multiplier (\(\lambda\)).
Note: Addition of Lagrangian function that incorporates the constraints,
makes the problem solvable using standard calculus.
e.g.:
Let f(x) be the objective function with single equality constraint \(g(x) = c\),
then the Lagrangian function \( \mathcal{L}\) is defined as:
Now, the above constrained optimization problem becomes an unconstrained optimization problem:
By solving the above unconstrained optimization problem,
we get the optimum solution for the original constrained problem.
Objective: To minimize the distance between point (x,y) on the line 2x + 3y = 13 and the origin (0,0).
distance, d = \(\sqrt{(x-0)^2 + (y-0)^2}\)
=> Objective function = minimize distance = \( \underset{x^*, y^*}{\mathrm{argmin}}\ f(x,y) =
\underset{x^*, y^*}{\mathrm{argmin}}\ x^2+y^2\)
Constraint: Point (x,y) must be on the line 2x + 3y = 13.
=> Constraint (equality) function = \(g(x,y) = 2x + 3y - 13 = 0\)
Lagragian function =
To find the optimum solution, we solve the below unconstrained optimization problem.
Take the derivative and equate it to zero.
Since, it is multi-variable function, we take the partial derivatives, w.r.t, x, y and \(\lambda\).
Now, we have 3 variables and 3 equations (1), (2) and (3), lets solve them.
Hence, the point (x=2, y=3) on the line 2x + 3y = 13 that is closest to the origin.
To solve the optimization problem, there are many methods, such as, analytical method, which gives the normal equation for the linear regression,
but we will discuss that method later in detail, when we have understood what is linear regression?
Normal Equation for linear regression:
X: Feature variables
y: Vector of all observed target values
End of Section
Till now, we have understood how to formulate a minimization problem as a mathematical optimization problem.
Now, lets take a step forward and understand how to solve these optimization problems.
We will focus on two important iterative gradient based methods:
Gradient Descent:
It is a first order iterative optimization algorithm that is used to find the local minimum of a differentiable function.
It iteratively adjusts the parameters of the model in the direction opposite to the gradient of cost function,
since moving opposite to the direction of gradient leads towards the minima.
Algorithm:
Initialize the weights/parameters with random values.
Calculate the gradient of the cost function at current parameter values.
Update the parameters using the gradient.
\[ w_{new} = w_{old} - \eta \cdot \frac{\partial f}{\partial w_{old}} \\[10pt] \eta: \text{ learning rate or step size to take for each parameter update} \]Repeat steps 2 and 3 iteratively until convergence (to minima).
There are 3 types of Gradient Descent:
Batch Gradient Descent (BGD):
Computes the gradient using all the data points in the dataset for parameter update in each iteration.
Say, number of data points in the dataset is \(n\).
Let, the loss function for individual data point be \(l_i(w)\)
Key Points:
Stochastic Gradient Descent (SGD):
It uses only 1 data point selected randomly from dataset to compute gradient for parameter update in each iteration.
Key Points:
Mini Batch Gradient Descent (MBGD):
It uses small randomly selected subsets of dataset, called mini-batch, (1<k<n) to compute gradient for
parameter update in each iteration.
Key Points:
End of SectionNewton’s Method:
It is a second-order iterative gradient based optimization technique known for its extremely fast convergence.
When close to optimum, it achieves quadratic convergence, better than gradient descent’s linear convergence.
Algorithm:
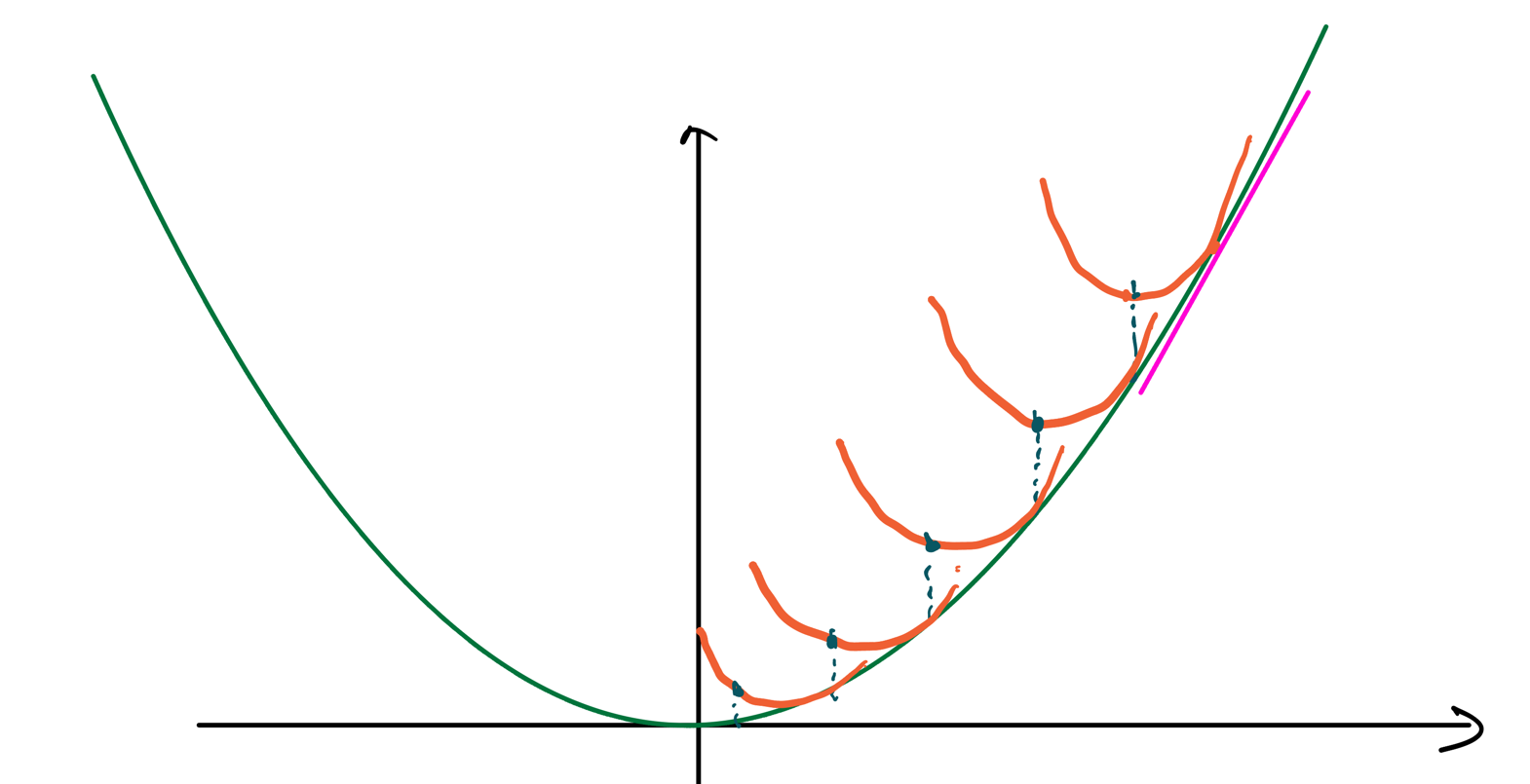
Now, we will solve this using Newton’s Method.
Let’s start at x = 0.
Hence, we can see that using Newton’s Method we can get to the minima \(x^* = 2\) in just 1 step.
Full Newton’s Method is rarely used in Machine Learning/Deep Learning optimization,
because of the following limitations:
Because of the above limitations, we use Quasi-Newton methods like BFGS and L-BFGS.
The quasi-Newton methods make use of approximations for Hessian calculation, in order to gain the benefits
of curvature without incurring the cost of Hessian calculation.
BFGS: Broyden-Fletcher-Goldfarb-Shanno
L-BFGS: Limited-memory BFGS
End of Section