Statistics for AI & ML
This sheet contains all the topics that will be covered for Statistics for AI & ML.
This is the multi-page printable view of this section. Click here to print.
This sheet contains all the topics that will be covered for Statistics for AI & ML.
Measures of Central Tendency:
A single number that describes the central, typical, or representative value of a dataset, e.g, mean, median, and mode.
The mean is the average, the median is the middle value in a sorted list, and the mode is the most frequently occurring value.
Mean:
The artihmetic average of a set of numbers i.e sum all values and divide by the number of values.
\(mean = \frac{1}{n}\sum_{i=1}^{n}x_i\)
Pros:
Cons:
For example:
Median:
The middle value of a sorted list of numbers. It divides the dataset into 2 equal halves.
Calculation:
Pros:
Cons:
For example:
Mode:
The most frequently occurring value in a dataset.
Pros:
Cons:
Range:
The difference between the largest and smallest values in a dataset. Simplest measure of dispersion
\(range = max - min\)
Pros:
Cons:
Variance:
The average of the squared distance of each value from the mean.
Measures the spread of data points.
\(sample ~ variance = s^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2\)
\(population ~ variance = \sigma^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \mu)^2\)
Cons:
Standard Deviation:
The square root of the variance, measures average distance of data points from the mean.
\(s = sample ~ standard ~ deviation \)
\(\sigma = population ~ standard ~ deviation \)
For example:
Mean Absolute Deviation:
It is the average of absolute deviation or distance of all data points from mean.
\( mad = \frac{1}{n}\sum_{i=1}^{n}|x_i - \bar{x}| \)
Pros:
For example:
Skewness:
It measures the asymmetry of a data distribution.
Tells us whether the data is concentrated on one side of mean and is there a long tail stretching on the other side.
Positive Skew:
Negative Skew:
Zero Skew:
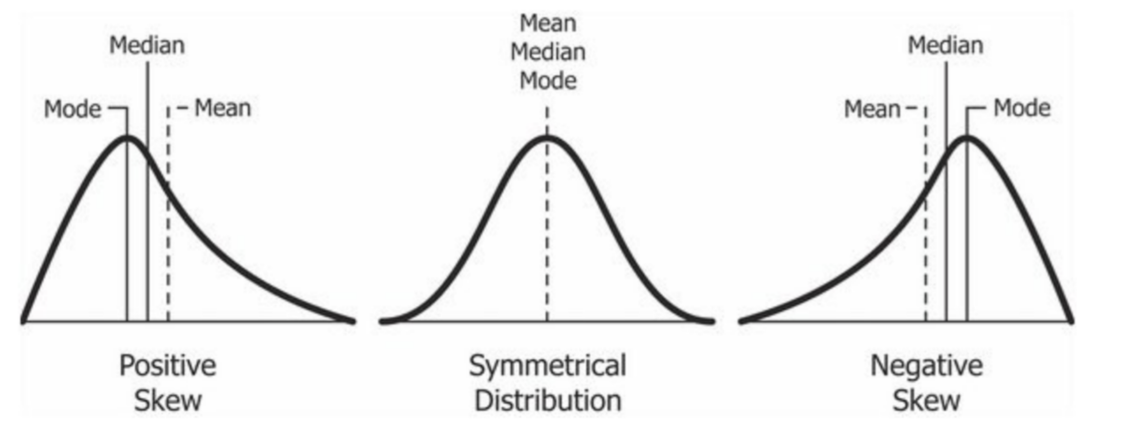
For example:
Kurtosis:
It measures the “tailedness” of a data distribution.
It describes how much the data is concentrated in tails (fat or thin) versus the center.
Excess Kurtosis:
Excess kurtosis is calculated by subtracting 3 from standard kurtosis in order to compare with normal distribution.
Normal distribution has kurtosis = 3.
Mesokurtic:
Leptokurtic:
Platykurtic:
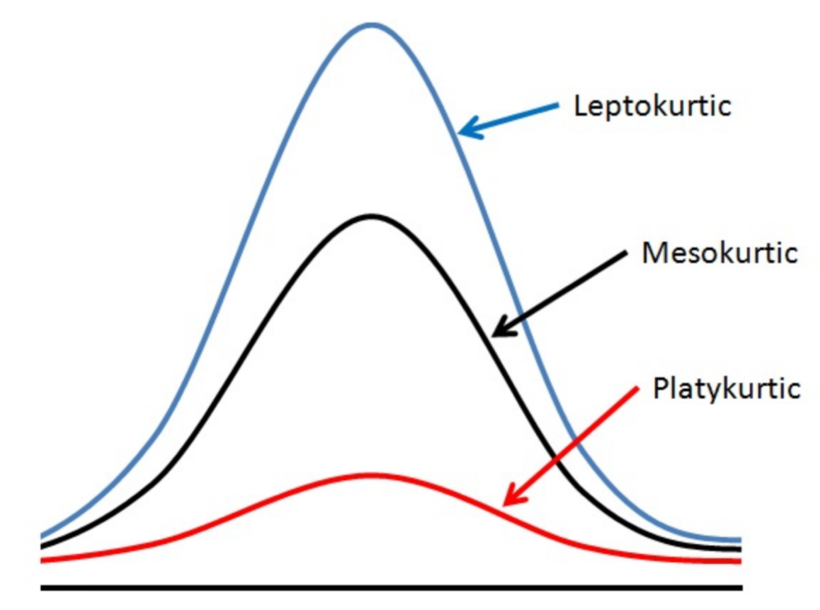
Percentile:
It indicates the percentage of scores in a dataset that are equal to or below a specific value.
Here, the complete dataset is divided into 100 equal parts.
Quartile:
They are special percentiles that divide the complete dataset into 4 equal parts.
Q1 => 25th percentile, value below which 25% of the data falls.
Q2 => 50th percentile, value below which 50% of the data falls; median.
Q3 => 75th percentile, value below which 75% of the data falls.
For example:
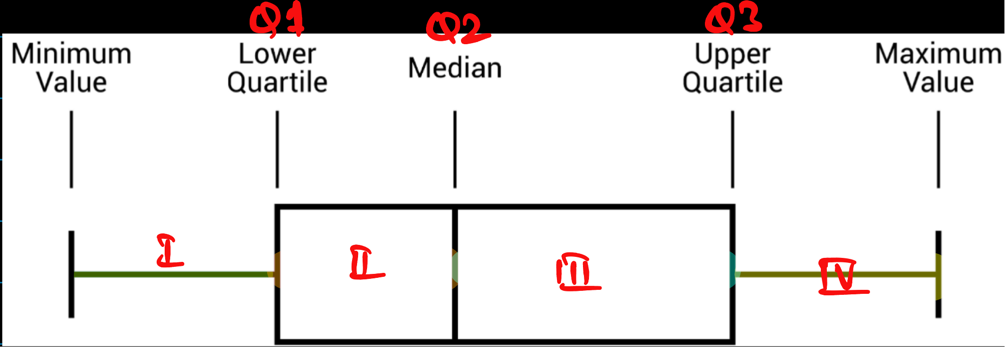
Inter Quartile Range(IQR):
It is the single number that measures the spread of middle 50% of the data, i.e Q1-Q3.
IQR = Q3 - Q1
For example:
Therefore, IQR = Q3-Q1 = 9-3 = 6
IQR is a standard tool for detecting outliers.
Values that fall outside the ‘fences’ can be considered as potential outliers.
Lower fence = Q1 - 1.5 * IQR
Upper fence = Q3 + 1.5 * IQR
IQR = Q3-Q1 = 9-3 = 6
Lower fence = Q1 - 1.5 * IQR = 3 - 9 = -6
Upper fence = Q3 + 1.5 * IQR = 9 + 9 = 18
So, any data point that is less than -6 or greater than 18 is considered as a potential outlier.
As in this example, 100 can be considered as an outlier.
Even though the above metrics give us a good idea of the data distribution,
but still we should always plot the data and visually inspect the data distribution.
As these metrics may not provide the complete picture.
A mathematician called Francis John Anscombe has illustrated this point beautifully in his Anscombe’s Quartet.
Anscombe’s quartet:
It comprises four datasets that have nearly identical simple descriptive statistics,
yet have very different distributions and appear very different when plotted.
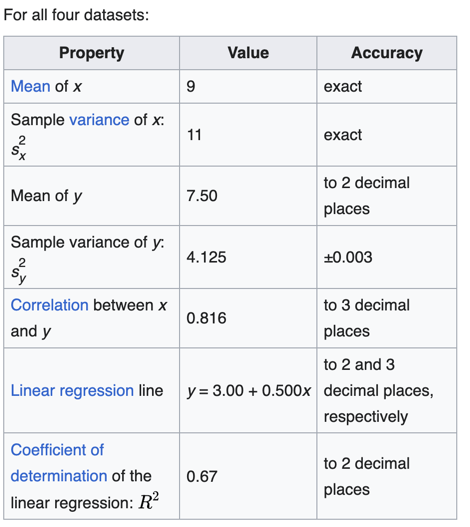
End of Section
Covariance:
It measures the direction of linear relationship between two variables \(X\) and \(Y\).
\(N\) = size of population
\(\mu_{x}\) = population mean of \(X\)
\(\mu_{y}\) = population mean of \(Y\)
\(n\) = size of sample
\(\bar{x}\) = sample mean of \(X\)
\(\bar{y}\) = sample mean of \(Y\)
Note: We have a term (n-1) instead of n in the denominator to make it an unbiased estimate, called Bessel’s Correction.
If both \((x_i - \bar{x})\) and \((y_i - \bar{y})\) have the same sign, then the product is positive(+ve).
If both \((x_i - \bar{x})\) and \((y_i - \bar{y})\) have opposite signs, then the product is negative(-ve).
The final value of covariance depends on the sum of the above individual products.
\( \begin{aligned} \text{Cov}(X, Y) &> 0 &&\Rightarrow \text{ } X \text{ and } Y \text{ increase or decrease together} \\ \text{Cov}(X, Y) &= 0 &&\Rightarrow \text{ } \text{No linear relationship} \\ \text{Cov}(X, Y) &< 0 &&\Rightarrow \text{ } \text{If } X \text{ increases, } Y \text{ decreases (and vice versa)} \end{aligned} \)
Limitation:
Covariance is scale-dependent, i.e, units of X and Y impact its magnitude.
This makes it hard to make comparisons of covariance across different datasets.
E.g: Covariance between age and height will NOT be same as the covariance between years of experience and salary.
Note:It only measures the direction of the relationship, but does NOT give any information about the strength of the relationship.
Correlation:
It measures both the strength and direction of the linear relationship between two variables \(X\) and \(Y\).
It is a standardized version of covariance that gives a dimensionless measure of linear relationship.
There are 2 popular ways to calculate correlation coefficient:
Pearson Correlation Coefficient (r):
It is a standardized version of covariance and most widely used measure of correlation.
Assumption: Data is normally distributed.
\(\sigma_{x}\) and \(\sigma_{y}\) are the standard deviations of \(X\) and \(Y\).
Range of \(r\) is between -1 and 1.
\(r = 1\) => perfect +ve linear relationship between X and Y
\(r = -1\) => perfect -ve linear relationship between X and Y
\(r = 0\) => NO linear relationship between X and Y.
Note: A correlation coefficient of 0.9 means that there is a strong linear relationship between X and Y,
irrespective of their units.
Let’s calculate the standard deviation of \(X\) and \(Y\):
\(\sigma_{x} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2} \)
\(= \sqrt{\frac{1}{3-1}[(1-2)^2 + (2-2)^2 + (3-2)^2]}\)
\(= \sqrt{\frac{1+0+1}{2}} =\sqrt{\frac{2}{2}} = 1 \)
Similarly, we can calculate the standard deviation of \(Y\):
\(\sigma_{y} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(y_i - \bar{y})^2} \)
\(= \sqrt{\frac{1}{3-1}[(2-4)^2 + (4-4)^2 + (6-4)^2]}\)
\(= \sqrt{\frac{4+0+4}{2}} =\sqrt{\frac{8}{2}} = 2 \)
Now, we can calulate the pearson correlation coefficient (r):
\(r_{xy} = \frac{Cov(X, Y)}{\sigma_{x} \sigma_{y}}\)
=> \(r_{xy} = \frac{2}{1* 2}\)
=> \(r_{xy} = 1\)
Therefore, we can say that there is a strong +ve linear relationship between X and Y.
Spearman Rank Correlation Coefficient (\(\rho\)):
It is a measure of the strength and direction of the monotonic relationship between two ranked variables \(X\) and \(Y\).
It captures monotonic relationship, meaning the variables move in the same or opposite direction,
but not necessarily a linear relationship.
| Student | Teacher A Rank | Teacher B Rank | \(d_i\) | \(d_i^2\) |
|---|---|---|---|---|
| S1 | 1 | 2 | -1 | 1 |
| S2 | 2 | 1 | 1 | 1 |
| S3 | 3 | 3 | 0 | 0 |
| S4 | 4 | 5 | -1 | 1 |
| S5 | 5 | 4 | 1 | 1 |
\(\sum_{i}d_i^2 = 4 \)
\( n = 5 \)
\(\rho_{xy} = 1 - \frac{6\sum_{i}d_i^2}{n(n^2-1)}\)
=> \(\rho_{xy} = 1 - \frac{6*4}{5(5^2-1)}\)
=> \(\rho_{xy} = 1 - \frac{24}{5*24}\)
=> \(\rho_{xy} = 1 - \frac{1}{5}\)
=> \(\rho_{xy} = 0.8\)
Therefore, we can say that there is a strong +ve correlation between the ranks given by teacher A and teacher B.
Correlation is very useful in feature selection for training machine learning models.
Causation means that one variable directly causes the change in another variable, i.e, direct
cause->effect relationship.
Whereas, correlation means that two variables move together.
E.g: Election results and stock market - there may be some correlation between the two,
but establishing clear causal links is difficult.
End of Section
Population Mean:
It is the true average of the entire group.
It describe the central tendency of the entire population.
\( \mu = \frac{1}{N}\sum_{i=1}^{N}x_i \)
N: Number of data points
Sample Mean:
It is the average of a smaller representative subset (a sample) of the entire population.
It provides an estimate of the population mean.
\( \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i \)
n: size of sample
Central Limit Theorem:
This law states that for a sequence of of I.I.D random variables \( X_1, X_2, \dots, X_n \),
with finite mean and variance, the distribution of the sample mean \( \bar{X} \) approaches a normal distribution
as \( n \rightarrow \infty \), regardless of its original population distribution.
The distribution of the sample mean is : \( \bar{X} \sim N(\mu, \sigma^2/n)\)
Let, \( X_1, X_2, \dots, X_n \) are I.I.D random variables.
Now, let’s calculate the variance of sample means.
We know that:
Let’s apply above 2 rules on the variance of sample means equation above:
\[ \begin{aligned} Var[\bar{X_n}] &= Var[\frac{1}{n}(X_1+ X_2+ \dots+ X_n)] \\ &= \frac{1}{n^2}[Var[X_1+ X_2+ \dots+ X_n]] \\ &= \frac{1}{n^2}[Var[X_1] + Var[X_2] + \dots + Var[X_n]] \\ \text{We know that: } Var[X_i] = \sigma^2 \\ &= \frac{1}{n^2}[\sigma^2 + \sigma^2 + \dots + \sigma^2] \\ &= \frac{n\sigma^2}{n^2} \\ => Var[\bar{X_n}] &= \frac{\sigma^2}{n} \end{aligned} \]Since, standard deviation = \(\sigma = \sqrt{Variance}\)
Therefore, Standard Deviation\([\bar{X_n}] = \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}\)
The standard deviation of the sample means is also known as “Standard Error”.
Note: We can also standardize the sample mean, i.e, mean centering and variance scaling.
Standardisation helps us to use the Z-tables of normal distribution.
We know that, a standardized random variable \(Y_i = \frac{X_i - \mu}{\sigma}\)
Similarly, standardized sample mean:
Note: For practical purposes, \(n \ge 30\) is considered as a sufficient sample size for the CLT to hold.
Note:
The variance must be finite, else, the sample mean will NOT converge to a normal distribution.
If a distribution has a heavy tail, then the expected value calculation diverges.
e.g:
End of Section
Confidence Interval:
It is a range of values that is likely to contain the true population mean, based on a sample.
Instead of giving a point estimate, it gives a range of values with confidence level.
For normal distribution, confidence interval :
\(\bar{X}\): Sample mean
\(Z\): Z-score corresponding to confidence level
\(n\): Sample size
\( \sigma \): Population Standard Deviation
Applications:
95% confidence interval does NOT mean there is a 95% chance that the true mean lies in the specific calculated interval.
For example:
Let’s suppose we want to measure the average weight of a certain species of dog.
We want to estimate the true population
mean \(\mu\) using confidence interval.
Note: True average weight = 30 kg, but this is NOT known to us.
| Sample Number | Sample Mean | 95% Confidence Interval | Did it capture \(\mu\) ? |
|---|---|---|---|
| 1 | 29.8 kg | (28.5, 31.1) | Yes |
| 2 | 30.4 kg | (29.1, 31.7) | Yes |
| 3 | 31.5 kg | (30.2, 32.8) | No |
| 4 | 28.1 kg | (26.7, 29.3) | No |
| - | - | - | - |
| - | - | - | - |
| - | - | - | - |
| 100 | 29.9 kg | (28.6, 31.2) | Yes |
Suggest which company is offering a better salary?
Below is the details of the salaries based on a survey of 50 employees.
| Company | Average Salary(INR) | Standard Deviation |
|---|---|---|
| A | 36 lpa | 7 lpa |
| B | 40 lpa | 14 lpa |
For comparison, let’s calculate the 95% confidence interval for the average salaries of both companies A and B.
We know that:
\( CI = \bar{X} \pm Z\frac{\sigma}{\sqrt{n}} \)
Margin of Error(MoE) \( = Z\frac{\sigma}{\sqrt{n}} \)
Z-Score for 95% CI = 1.96
\(MoE_A = 1.96*\frac{7}{\sqrt{50}} \approx 1.94 \)
=> 95% CI for A = \(36 \pm 1.94 \) = [34.06, 37.94]
\(MoE_B = 1.96*\frac{14}{\sqrt{50}} \approx 3.88\)
=> 95% CI for B = \(40 \pm 3.88 \) = [36.12, 43.88]
We can see that initially company B’s salary looked obviously better,
but after calculating the 95% CI, we can see that there is a significant overlap in the salaries of two companies,
i.e [36.12, 37.94].
End of Section
Hypothesis Testing is used to determine whether a claim or theory about a population is supported by a sample data,
by assessing whether observed difference or patterns are likely due to chance or represent a true effect.
Hypothesis Testing:
It is a statistical inference framework used to make decisions about a population parameter, such as, the mean, variance,
distribution, correlation, etc., based on a sample of data.
It provides a formal method to evaluate competing claims.
Null Hypothesis (\(H_0\)):
Status quo or no-effect or no difference statement; almost always contains a statement of equality.
Alternative Hypothesis (\(H_1 ~or~ H_a\)):
The statement representing an effect, a difference, or a relationship.
It must be true if the null hypothesis is rejected.
Say, the data, D: <patient_id, med_1/med_2, recovery_time(in days)>
We need some metric to compare the recovery times of 2 medicines.
We can use the mean recovery time as the metric, because we know that we can use following techniques for comparison:
Note: Let’s assume the sample size \(n < 30\), because medical tests usually have small sample sizes.
=> We will use the 2-Sample T-Test; we will continue using T-Test throughout the discussion.
Step 1: Define the null and alternative hypotheses.
Null Hypothesis \(H_0\): The mean recovery time of 2 medicines is the same i.e \(Mean_{m1} = Mean_{m2}\) or \(m_{m1} = m_{m2}\).
Alternate Hypothesis \(H_a\): \(m_{m1} < m_{m2}\) (1-Sided T-Test) or \(m_{m1} ⍯ m_{m2}\) (2-Sided T-Test).
Step 2: Select a relevant statistical test for the task with associated test statistic.
Let’s do a 2 sample T-Test, i.e, \(m_{m1} < m_{m2}\)
Step 3: Calculate the test statistic under null hypothesis.
Test Statistic:
For 2 sample T-Test:
s: Standard Deviation
n: Sample Size
Note: If the 2 means are very close then \(t_{obs} \approx 0\).
Step 4: Suppose significance level (\(\alpha\)) = 5% or 0.05.
Step 5: Compute the p-value from the observed value of test-statistic.
P-Value:
p-value = area under curve = probability of observing test statistic \( \ge t_{obs} \) if the null hypothesis is true.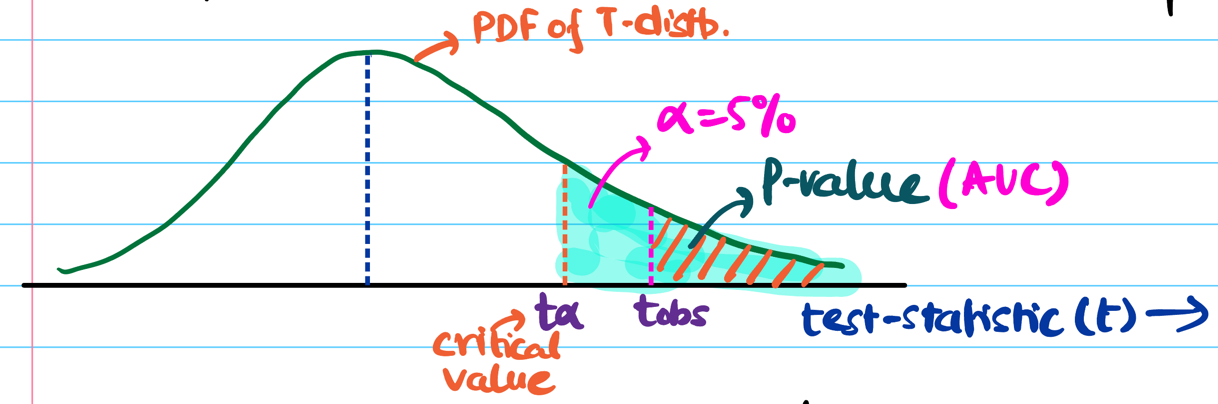
Step 6: Accept or reject the null hypothesis, based on the significance level (\(\alpha\)).
If \(p_{value} < \alpha\), we reject the null hypothesis and accept the alternative hypothesis and vice versa.
Note: In the above example \(p_{value} < \alpha\), so we reject the null hypothesis.
We need to do a left or right sided test, or a 2-sided test, this depends upon our alternate hypothesis and test statistic.
Let’s continue our 2 sample mean T-test to understand the concept:
Left Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 < medicine 2, i.e, \(m_{m_1} < m_{m_2}\)
=> \(m_{m_1} - m_{m_2} < 0\)
Since, the denominator in above equation is always positive.
=> \(t_{obs} < 0\)
Therefore, we need to do a left sided/tailed test.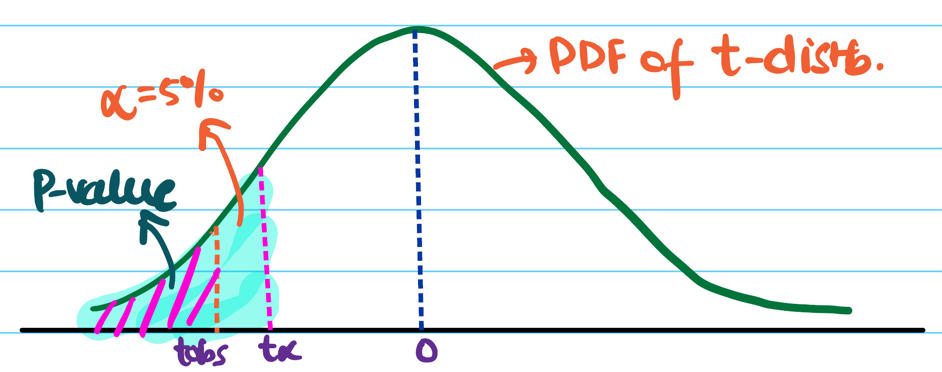
So, we want \(t_{obs}\) to be very negative to confidently conclude that alternate hypothesis is true.
Right Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 > medicine 2, i.e, \(m_{m_1} > m_{m_2}\)
=> \(m_{m_1} - m_{m_2} > 0\)
Similarly, here we need to do a right sided/tailed test.
2 Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 ⍯ medicine 2, i.e, \(m_{m_1} ⍯ ~ m_{m_2}\)
=> \(m_{m_1} - m_{m_2} < 0\) or \(m_{m_1} - m_{m_2} > 0\)
If \(H_a\) is true then \(t_{obs}\) is a large -ve value or a large +ve value.
Since, t-distribution is symmetric, we can divide the significance level \(\alpha\) into 2 equal parts.
i.e \(\alpha = 2.5\%\) on each side.
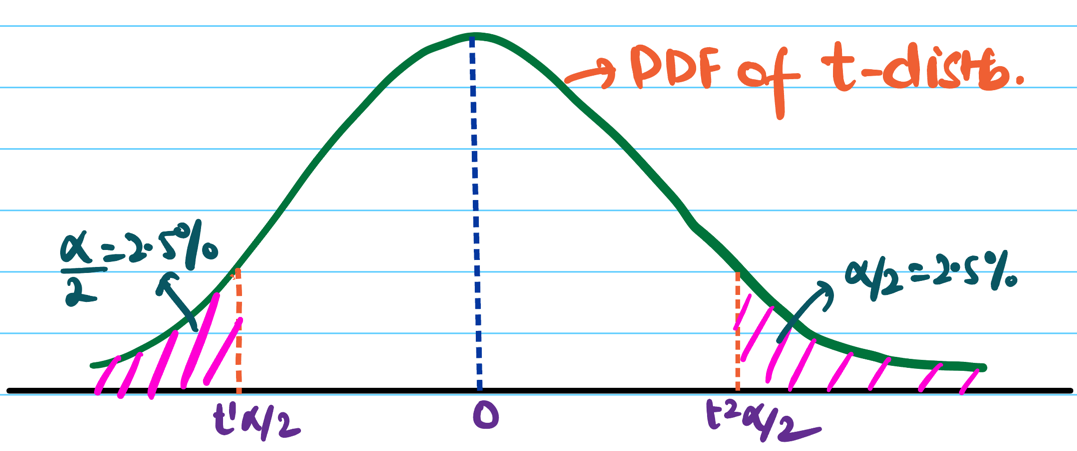
So, we want \(t_{obs}\) to be very negative or very positive to confidently conclude that the alternate hypothesis is true.
We accept \(H_a\) if \(t_{obs} < t^1_{\alpha/2}\) or \(t_{obs} > t^2_{\alpha/2}\).
Note: For critical applications ‘\(\alpha\)’ can be very small i.e. 0.1% or 0.01%, e.g medicine.
Significance Level (\(\alpha\)):
It is the probability of wrongly rejecting a true null hypothesis, known as a Type I error or false +ve rate.
Critical Value:
It is a specific point on the test-statistic distribution that defines the boundaries of the null hypothesis
acceptance/rejection region.
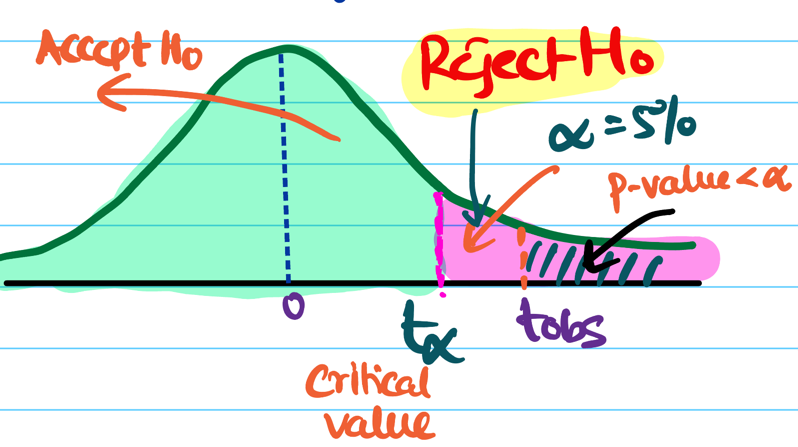
Power of Test:
It is the probability that a hypothesis test will correctly reject a false null hypothesis (\(H_{0}\))
when the alternative hypothesis (\(H_{a}\)) is true.

Yes, having a large sample size makes a hypothesis test more powerful.
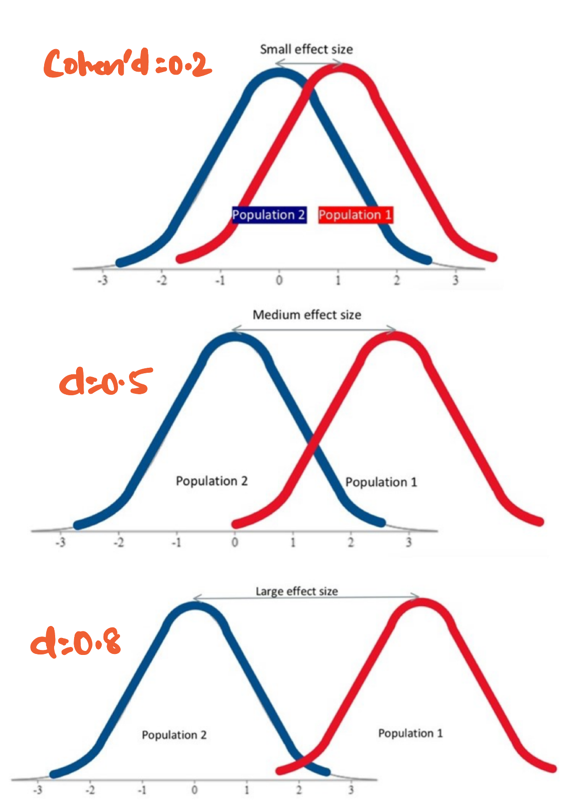
Effect Size:
It is a standardized objective measure that complements p-value by clarifying whether a statistically significant
finding has any real world relevance.
It quantifies the magnitude of relationship between two variables.
Effect size is measured using Cohen’s d formula:
\(\bar{X}\): Sample mean
\(s_p\): Pooled Standard deviation
\(n\): Sample size
\(s\): Standard deviation
Note: Theoretically, Cohen’s d value can range from negative infinity to positive infinity.
but for practical purposes, we use the following value:
small effect (\(d=0.2\)), medium effect (\(d=0.5\)), and large effect (\(d\ge 0.8\)).
End of Section
T-Test:
It is a statistical test that is used to determine whether the sample mean is equal to a hypothesized value or
is there a significant difference between the sample means of 2 groups.
Student’s t-distribution:
It is a continuous probability distribution that is a symmetrical, bell-shaped curve similar
to the normal distribution but with heavier tails.
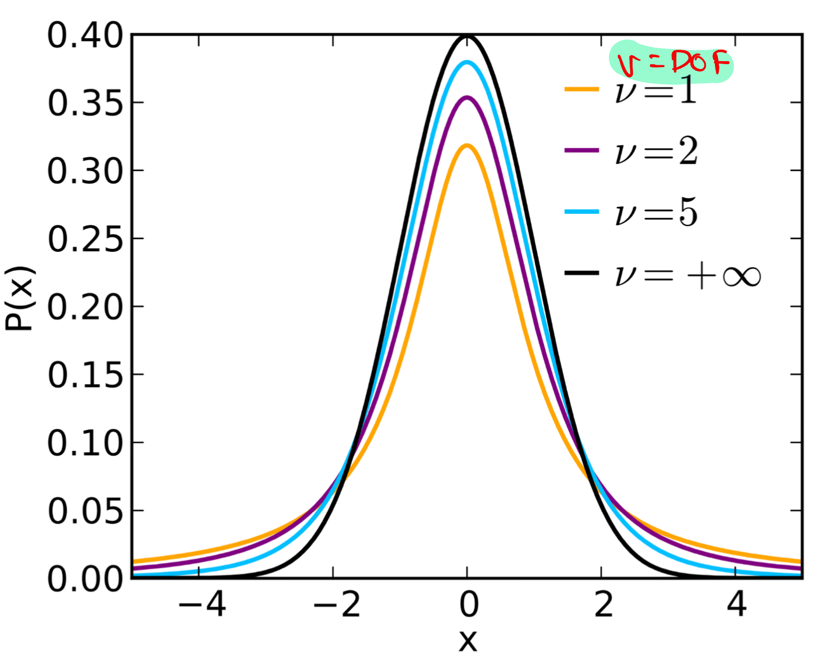
There are 3 types of T-Test:
1-Sample T-Test:
It is used to test whether the sample mean is equal to a known/hypothesized value.
Test statistic (t):
where,
\(\bar{x}\): sample mean
\(\mu\): hypothesized value
\(s\): sample standard deviation
\(n\): sample size
\(\nu = n-1 \): degrees of freedom
Let’s verify developer’s claim using the tester’s test results using 1 sample t-test.
Null hypothesis: \(H_0\) = The average API response time is 100 ms, i.e, \(\bar{x} = \mu\).
Alternative hypothesis: \(H_a\) = The average API response time > 100 ms, i.e, \(\bar{x} > \mu\) => right tailed test.
Hypothesized mean \(\mu\) = 100 ms
Sample mean \(\bar{x}\) = 115 ms
Sample standard deviation \(s\) = 25 ms
Sample size \(n\) = 20
Degrees of freedom \(\nu\) = 19
\( t_{obs} = \frac{\bar{x} - \mu}{s/\sqrt{n}}\) = \(\frac{115 - 100}{25/\sqrt{20}}\)
= \(\frac{15\sqrt{20}}{25} = \frac{3\sqrt{20}}{5} \approx 2.68\)
Let significance level \(\alpha\) = 5% =0.05.
Critical value \(t_{0.05}\) = 1.729
Important: Find the value of \(t_{\alpha}\) in T-table
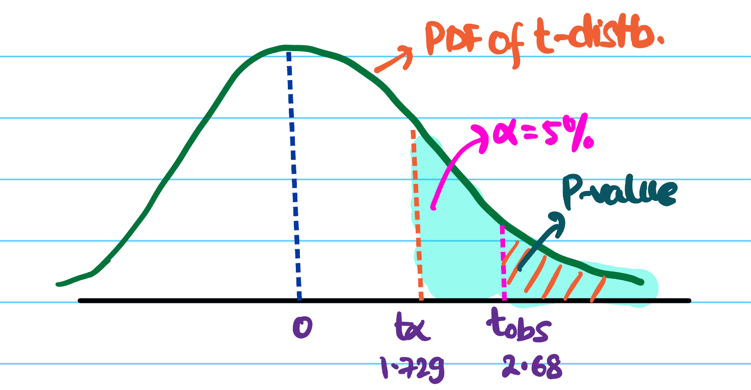
Since \(t_{obs}\) > \(t_{0.05}\), we reject the null hypothesis.
And, accept the alternative hypothesis that the API response time is significantly > 100 ms.
Hence, the developer’s claim is NOT valid.
2-Sample T-Test:
It is used to determine whether there is a significant difference between the means of two independent groups.
There are 2 types of 2-sample t-test:
Unequal Variance:
In this case, the variance of 2 independent groups is not equal.
Also called, Welch’s t-test.
Test statistic (t):
Equal Variance:
In this case, both samples come from equal or approximately equal variance.
Test statistic (t):
Here, degrees of freedom (for equal variance) \(\nu\) = \(n_1 + n_2 - 2\).
\(\bar{x}\): sample mean
\(s\): sample standard deviation
\(n\): sample size
\(\nu\): degrees of freedom
The AI team wants to validate whether the new ML model accuracy is better than the existing model’s accuracy.
Below is the data for the existing model and the new model.
| New Model (A) | Existing Model (B) | |
|---|---|---|
| Sample size (n) | 24 | 18 |
| Sample mean (\(\bar{x}\)) | 91% | 88% |
| Sample std. dev. (s) | 4% | 3% |
Given that the variance of accuracy scores of new and existing models are almost same.
Now, let’s follow our hypothesis testing framework.
Null hypothesis: \(H_0\): The accuracy of new model is same as the accuracy of existing model.
Alternative hypothesis: \(H_a\): The new model’s accuracy is better/greater than the existing model’s accuracy => right tailed test
Let’s solve this using 2 sample T-Test, since the sample size n < 30.
Since the variance of 2 sample are almost equal then we can use the pooled variance method.
Next let’s compute the test statistic, under null hypothesis.
DOF \(\nu\) = \(24+18-2\) = 42 - 2 = 40
Let significance level \(\alpha\) = 5% =0.05.
Critical value \(t_{0.05}\) = 1.684
Important: Find the value of \(t_{\alpha}\) in T-table
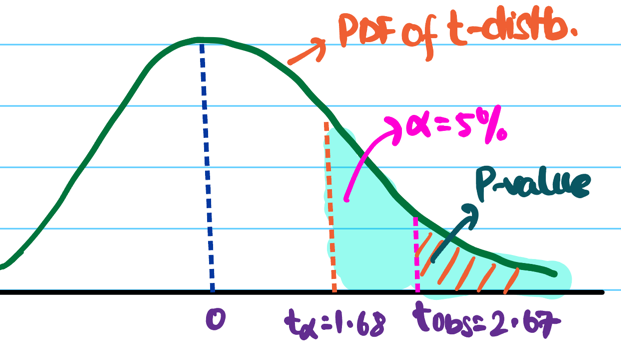
Since \(t_{obs}\) > \(t_{0.05}\), we reject the null hypothesis.
And, accept the alternative hypothesis that the new model has better accuracy than the existing model.
End of Section
Z-Test:
It is a statistical test used to determine whether there is a significant difference between mean of 2 groups or sample and population mean.
There are 2 types of Z-Test:
Z-Score:
It is a standardized score that measures how many standard deviations a particular data point is away from the population mean \(\mu\).
Z-score is calculated as:
\[Z = \frac{x - \mu}{\sigma}\]x: data point
\(\mu\): population mean
\(\sigma\): population standard deviation
e.g:
Z-score helps to define probability areas:
Note:
1-Sample Z-Test:
It is used to test whether the sample mean \(\bar{x}\) is significantly different from a known population mean \(\mu\).
Test Statistic:
\(\bar{x}\): sample mean
\(\mu\): hypothesized population mean
\(\sigma\): population standard deviation
\(n\): sample size
\(\sigma / \sqrt{n}\): standard error of mean
Read more about Standard Error
Note: Test statistic Z follows a standard normal distribution \(Z \sim \mathcal{N}(0, 1)\).
2-Sample Z-Test:
It is used to test whether the sample means \(\bar{x_1}\) and \(\bar{x_2}\) of 2 independent samples are significantly different from each other.
Test Statistic:
\(\bar{x_1}\): sample mean of first sample
\(\bar{x_2}\): sample mean of second sample
\(\sigma_1\): population standard deviation of first sample
\(\sigma_2\): population standard deviation of second sample
\(n_1\): sample size of first sample
\(n_2\): sample size of second sample
Note: Test statistic Z follows a standard normal distribution \(Z \sim \mathcal{N}(0, 1)\).
Null Hypothesis: \(\mu = 120\) seconds, i.e, no change.
Alternative Hypothesis: \(\mu < 120\) seconds => left tailed test.
We will use 1-sample Z-Test to test the hypothesis.
Test Statistic:
Since, significance level \(\alpha\) = 5% =0.05.
Critical value \(Z_{0.05}\) = -1.645
Important: Find the value of \(Z_{\alpha}\) in Z-Score Table
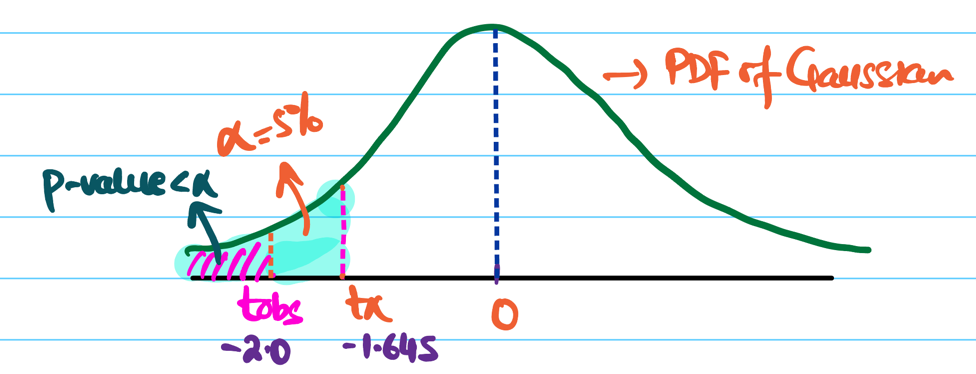
Our \(t_{obs}\) is much more extreme than the the critical value \(Z_{0.05}\), => p-value < 5%.
Hence, we reject the null hypothesis.
Therefore, there is a statistically significant evidence that the new optimisation reduces the runtime of the model.
Z Test of Proportion:
It is a statistical hypothesis test used to determine if there is a significant difference between the proportion
of a characteristic in two independent samples or to compare a sample proportion to a known population value
It is of 2 types:
The categorical data,i.e success/failure, is discrete that can be modeled as Bernoulli distribution.
Let’s understand how this Bernoulli random variable can be approximated as a Gaussian distribution for a very large sample size,
using Central Limit Theorem.
Read more about Central Limit Theorem
Note:We will not prove the complete thing, but we will understand the concept in enough depth for clarity.
\(Y \sim Bernoulli(p)\)
\(X \sim Binomial(n,p)\)
E[X] = mean = np
Var[X] = variance = np(1-p)
X = total number of successes
p = true probability of success
n = number of trials
Proportion of Success in sample = Sample Proportion = \(\hat{p} = \frac{X}{n}\)
e.g.: If n=100 people were surveyed, and 40 said yes, then \(\hat{p} = \frac{40}{100} = 0.4\)
By Central Limit Theorem, we can state that for very large ’n’ Binomial distribution’s mean and variance can be used as an
approximation for Gaussian/Normal distribution:
Since, \(\hat{p} = \frac{X}{n}\)
We can say that:
Mean = \(\mu_{\hat{p}} = p\) = True proportion of success in the entire population
Standard Error = \(SE_{\hat{p}} = \sqrt{Var[\frac{X}{n}]} = \sqrt{\frac{p(1-p)}{n}}\) = Standard Deviation of the sample proportion
Note: Large Sample Condition - Approximation is only valid when the expected number of successes and failures are both > 10 (sometimes 5).
\(np \ge 10 ~and~ n(1-p) \ge 10\)
1-Sample Z-Test of Proportion:
It is used to test whether the observed proportion in a sample differs from hypothesized proportion.
\(\hat{p} = \frac{X}{n}\): Proportion of success observed in a sample
\(p_0\): Specific propotion value under the null hypothesis
\(SE_0\): Standard error of sample proportion under the null hypothesis
Z-Statistic: Measures how many standard errors is the observed sample proportion \(\hat{p}\) away from \(p_0\)
Test Statistic:
2-Sample Z-Test of Proportion:
It is used to compare whether the 2 independent samples differ in their proportions.
A company wants to compare its 2 different website designs A & B.
Below is the table that shows the data:
| Design | # of visitors(n) | # of signups(x) | conversion rate(\(\hat{p} = \frac{x}{n}\)) |
|---|---|---|---|
| A | 1000 | 80 | 0.08 |
| B | 1200 | 114 | 0.095 |
Is the design B better, i.e, design B increases conversion rate or proportion of visitors who sign up?
Consider the significance level of 5%.
Null Hypothesis: \(\hat{p_A} = \hat{p_B}\), i.e, no difference in conversion rates of 2 designs A & B.
Alternative Hypothesis: \(\hat{p_B} > \hat{p_A}\) i.e conversion rate of B > A => right tailed test.
Check large sample condition for both samples A & B.
\(n\hat{p_A} = 80 > 10 ~and~ n(1-\hat{p_A}) = 920 > 10\)
Similarly, we can show for B too.
Pooled proportion:
\[ \bar{p} = \frac{x_A+x_B}{n_A+n_B} = \frac{80+114}{1000+1200} = \frac{194}{2200} \\[10pt] => \bar{p}\approx 0.0882 \]Standard Error(Pooled):
\[ SE=\sqrt{\bar{p}(1-\bar{p})(\frac{1}{n_1} +\frac{1}{n_2})} \\[10pt] = \sqrt{0.0882(1-0.0882)(\frac{1}{1000} +\frac{1}{1200})} \\[10pt] => SE \approx 0.0123 \]Test Statistic(Z):
\[ t_{obs} = \frac{\hat{p_B}-\hat{p_A}}{SE_{\hat{p_A}-\hat{p_B}}} \\[10pt] = \frac{0.095-0.0882}{0.0123} \\[10pt] => t_{obs} \approx 1.22 \]Significance level \(\alpha\) = 5% =0.05.
Critical value \(Z_{0.05}\) = 1.645
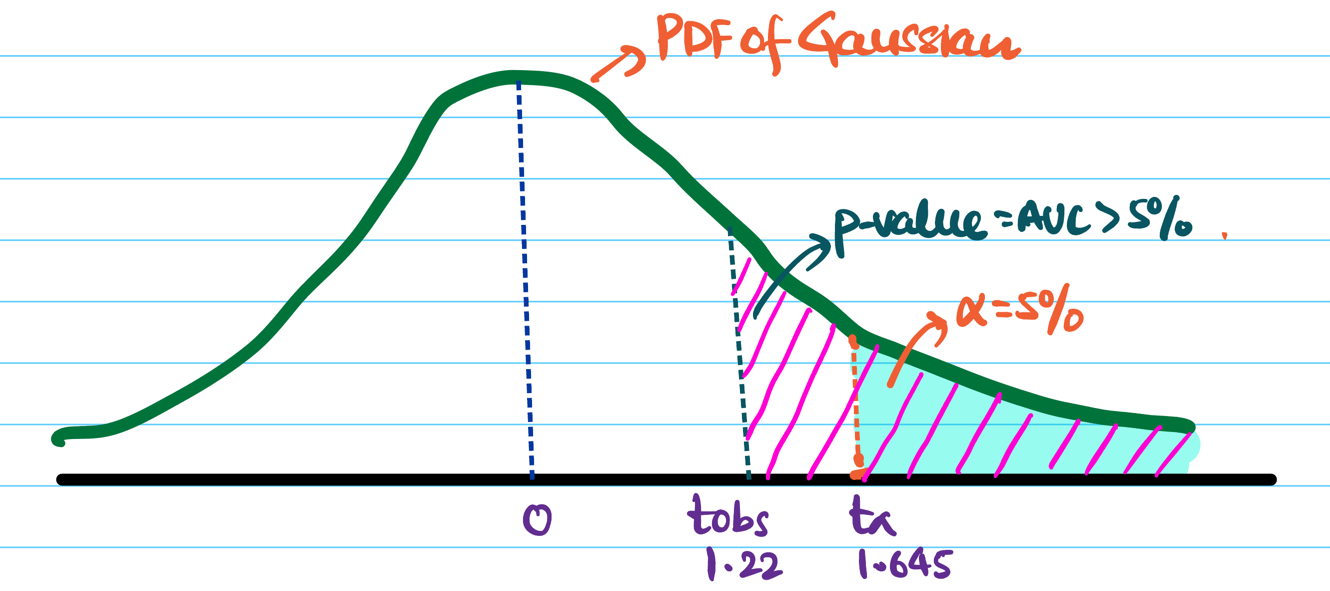
Since, \(t_{obs} < Z_{0.05}\) => p-value > 5%.
Hence, we fail to reject the null hypothesis.
Therefore, the observed conversion rate of design B is due to random chance; thus, B is not a better design.
End of Section
Chi-Square Distribution (\(\chi^2\)):
A random variable Q is said to follow a chi-square distribution with ’n’ degrees of freedom,i.e \(\chi^2(n)\),
if it is the sum of squares of ’n’ independent random variables that follow a standard normal distribution, i.e, \(N(0,1)\).
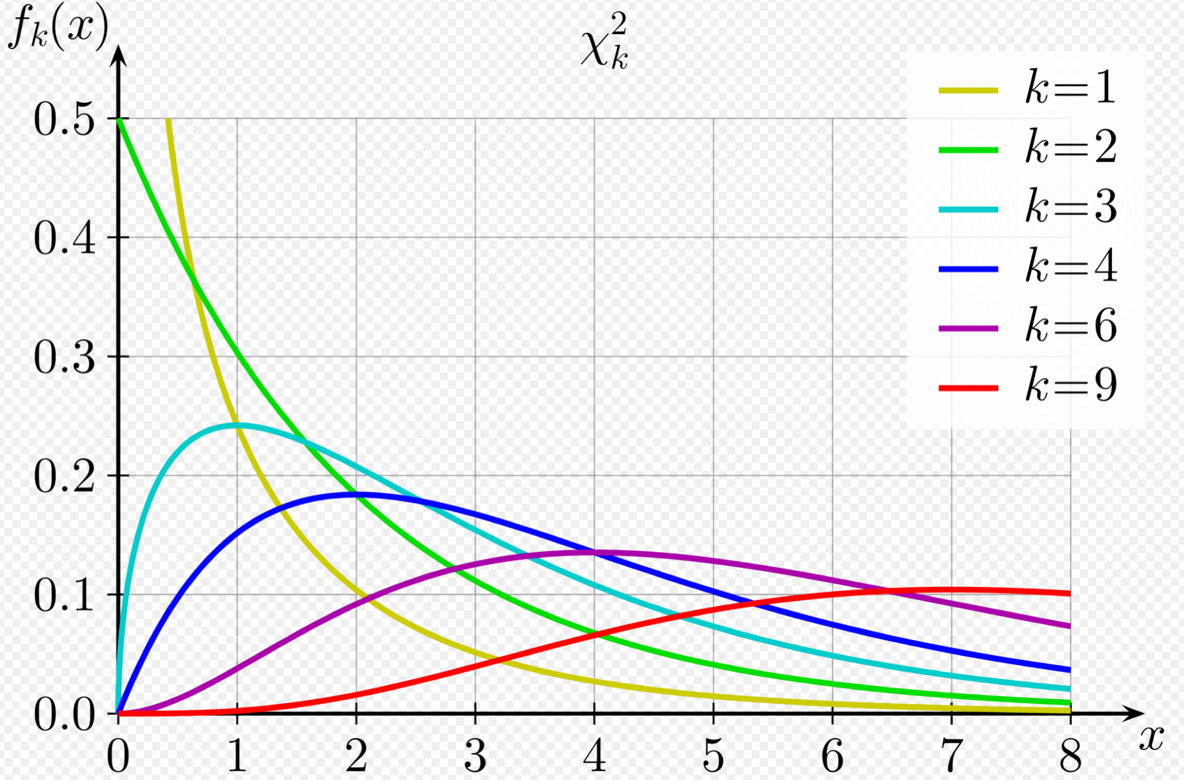
Key Properties:
Note: We are dealing with categorical data, where there is a count associated with each category.
In the context of categorical data, the counts \(O_i\) are governed by multinomial distribution
(a generalisation of binomial distribution).
Multinomial distribution is defined for multiple classes or categories, ‘k’, and multiple trials ’n’.
For \(i^{th}\) category:
Probability of \(i^{th}\) category = \(p_i\)
Mean = Expected count/frequency = \(E_i = np_i \)
Variance = \(Var_i = np_i(1-p_i) \)
By Central Limit Theorem, for very large n, i.e, as \(n \rightarrow \infty\), the multinomial distribution can be approximated as a normal distribution.
The multinomial distribution of count/frequency can be approximated as :
\(O_i \approx N(np_i, np_i(1-p_i))\)
Standardized count (mean centered and variance scaled):
Under Null Hypothesis:
In Pearson’s proof of the chi-square test, the statistic is divided by the expected value (\(E_{i}\)) instead of the variance (\(Var_{i}\)),
because for count data that can be modeled using a Poisson distribution
(or a multinomial distribution where cell counts are approximately Poisson for large samples),
the variance is equal to the expected value (mean).
Therefore, \(Z_i \approx (O_{i}-E_{i})/\sqrt{E_{i}}\)
Note that the denominator is \(\sqrt{E_{i}}\) NOT \(\sqrt{Var_{i}}\).
\(O_{i}\): Observed count for \(i^{th}\) category
\(E_{i}\): Expected count for \(i^{th}\) category
Important: \(E_{i}\): Expected count should be large i.e >= 5 (typically) for a good enough approximation.
Chi-Square (\(\chi^2\)) Test Statistic:
It is formed by squaring the approximately standard normal counts above, and summing them up.
For \(k\) categories, the test statistic is:
Note: For very large ’n’, the Pearson’s chi-square (\(\chi^2\)) test statistic follows a chi-square (\(\chi^2\)) distribution.
Test of Goodness of Fit:
It is used to compare the observed frequency distribution of a single categorical variable to a hypothesized or expected
probability distribution.
It can be used to determine whether a sample taken from a population follows a particular distribution,
e.g., uniform, normal, etc.
Test Statistic:
\(O_{i}\): Observed count for \(i^{th}\) category
\(E_{i}\): Expected count for \(i^{th}\) category, under null hypothesis \(H_0\)
\(k\): Number of categories
\(\nu\): Degrees of freedom = k - 1- m
\(m\): Number of parameters estimated from sample data to determine the expected probability
Note: Typical m=0, since, NO parameters are estimated.
We need to find whether the coin is fair i.e we need to do a goodness of fit test for discrete uniform distribution.
Null Hypothesis \(H_0\): Coin is fair.
Alternative Hypothesis \(H_a\): Coin is biased towards head.
\(O_{H}\): Observed count head = 62
\(O_{T}\): Observed count head = 38
\(E_{i}\): Expected count for \(i^{th}\) category, under null hypothesis \(H_0\) = 50 i.e fair coin
\(k\): Number of categories = 2
\(\nu\): Degrees of freedom = k - 1- m = 2 - 1 - 0 = 1
Test Statistic:
Since, significance level = 5% = 0.05
Critical value = \(\chi^2(0.05,1)\) = 3.84
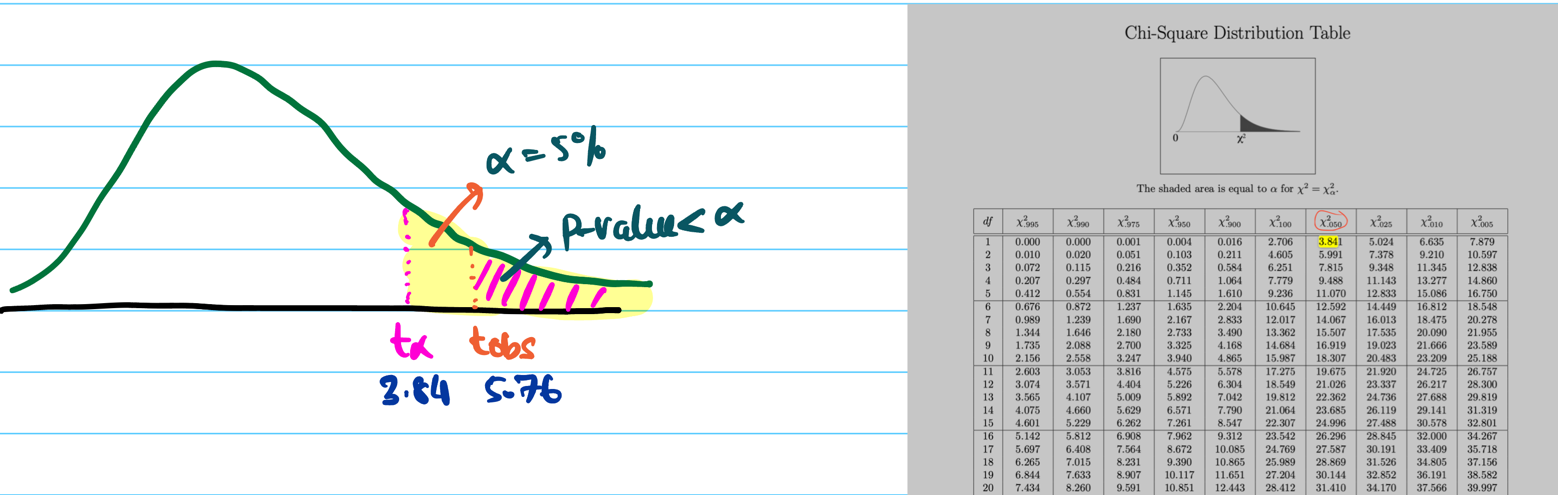
Since, \(t_{obs}\) = 5.76 > 3.84 (critical value), we reject the null hypothesis \(H_0\).
Therefore, the coin is biased towards head.
Test of Independence:
It is used to determine whether an association exists between two categorical variables,
using a contingency(dependency) table.
It is a non-parametric test, i.e, does NOT make any assumption about the underlying distribution of the data.
Test Statistic:
\(O_{ij}\): Observed count for \(cell_{i,j}\)
\(E_{ij}\): Expected count for \(cell_{i,j}\), under null hypothesis \(H_0\)
\(R\): Number of rows
\(C\): Number of columns
\(\nu\): Degrees of freedom = (R-1)*(C-1)
Let’s understand the above test statistic in more detail.
We know that, if 2 random variables A & B are independent, then,
\(P(A \cap B) = P(A, B) = P(A)*P(B)\)
i.e Joint Probability = Product of marginal probabilities.
Null Hypothesis \(H_0\): \(A\) and \(B\) are independent.
Alternative Hypothesis \(H_a\): \(A\) and \(B\) are dependent or associated.
N = Sample size
\(P(A_i) \approx \frac{Row ~~ Total_i}{N}\)
\(P(B_j) \approx \frac{Col ~~ Total_j}{N}\)
\(E_{ij}\) : Expected count for \(cell_{i,j}\) = \( N*P(A_i)*P(B_j)\)
=> \(E_{ij}\) = \(N*\frac{Row ~~ Total_i}{N}*\frac{Col ~~ Total_j}{N}\)
=> \(E_{ij}\) = \(\frac{Row ~~ Total_i * Col ~~ Total_j}{N}\)
\(O_{ij}\): Observed count for \(cell_{i,j}\)
A survey of 100 students was conducted to understand whether there is any relation between gender and beverage preference.
Below is the table that shows the number of students who prefer each beverage.
| Gender | Tea | Coffee | |
|---|---|---|---|
| Male | 20 | 30 | 50 |
| Female | 10 | 40 | 50 |
| 30 | 70 |
Significance level = 5%
Null Hypothesis \(H_0\): Gender and beverage preference are independent.
Alternative Hypothesis \(H_a\): Gender and beverage preference are dependent.
We know that Expected count for cell(i,j) = \(E_{ij}\) = \(\frac{Row ~~ Total_i * Col ~~ Total_j}{N}\)
\(E_{11} = \frac{50*30}{100} = 15\)
\(E_{12} = \frac{50*70}{100} = 35\)
\(E_{21} = \frac{50*30}{100} = 15\)
\(E_{22} = \frac{50*70}{100} = 35\)
Test Statistic:
Degrees of freedom = (R-1)(C-1) = (2-1)(2-1) = 1
Since, significance level = 5% = 0.05
Critical value = \(\chi^2(0.05,1)\) = 3.84
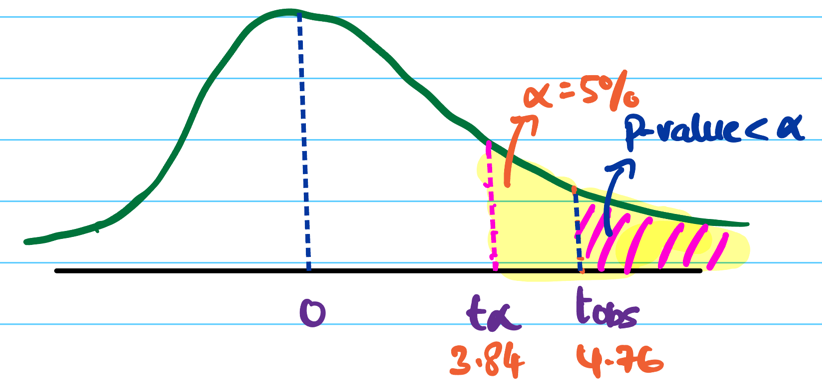
Since, \(t_{obs}\) = 4.76 > 3.84 (critical value), we reject the null hypothesis \(H_0\).
Therefore, the gender and beverage preference are dependent.
End of Section
Confusion Matrix:
It is a table that summarizes model’s predictions against the actual class labels, detailing where the model
succeeded and where it failed.
It is used for binary or multi-class classification problems.
| Predicted Positive | Predicted Negative | |
|---|---|---|
| Actual Positive | True Positive (TP) | False Negative (FN) |
| Actual Negative | False Positive (FP) | True Negative (TN) |
Type-1 Error:
It is the number of false positives.
e.g.: Model predicted that a patient has diabetes, but the patient actually does NOT have diabetes; “false alarm”.
Type-2 Error:
It is the number of false negatives.
e.g.: Model predicted that a patient does NOT have diabetes, but the patient actually has diabetes; “a miss”.
Many metrics are derived from the confusion matrix.
Precision:
It answers the question: “Of all the instances that the model predicted as positive, how many were actually positive?”
It measures exactness or quality of the positive predictions.
Recall:
It answers the question: “Of all the actual positive instances, how many did the model correctly identify?”
It measures completeness or coverage of the positive predictions.
F1 Score:
It is the harmonic mean of precision and recall.
It is used when we need a balance between precision and recall; also helpful when we have imbalanced data.
Harmonic mean penalizes extreme values more heavily, encouraging both metrics to be high.
| Precision | Recall | F1 Score | Mean |
|---|---|---|---|
| 0.5 | 0.5 | 0.50 | 0.5 |
| 0.7 | 0.3 | 0.42 | 0.5 |
| 0.9 | 0.1 | 0.18 | 0.5 |
Trade-Off:
Precision Focus:: Critical when cost of false positives is high.
e.g: Identify a potential terrorist.
A false positive, i.e, wrongly flagging an innocent person as a potential terrorist is very harmful.
Recall Focus:: Critical when cost of false negatives is high.
e.g.: Medical diagnosis of a serious disease.
A false negative, i.e, falsely missing a serious disease can cost someone’s life.
Analyze the performance of an access control system. Below is the data for 1000 access attempts.
| Predicted Authorised Access | Predicted Unauthorised Access | |
|---|---|---|
| Actual Authorised Access | 90 (TP) | 10 (FN) |
| Actual Unauthorised Access | 1 (FP) | 899 (TN) |
When the system allows access, it is correct 98.9% of the time.
The system caught 90% of all authorized accesses.
Receiver Operating Characteristic (ROC) Curve:
It is a graphical plot that shows the discriminating ability of a binary classifier system, as its
discrimination threshold is varied.
Y-axis: True Positive Rate (TPR), Recall, Sensitivity
\(TPR = \frac{TP}{TP + FN}\)
X-axis: False Positive Rate (FPR); (1 - Specificity)
\(FPR = \frac{FP}{FP + TN}\)
Note: A binary classifier model outputs a probability score between 0 and 1.
and a threshold (default=0.5) is applied to the probability score to get the final class label.
\(p \ge 0.5\) => Positive Class
\(p < 0.5\) => Negative Class
Algorithm:
e.g.:
| Patient_Id | True Label \(y_i\) | Predicted Probability Score \(\hat{y_i}\) |
|---|---|---|
| 1 | 1 | 0.95 |
| 2 | 0 | 0.85 |
| 3 | 1 | 0.72 |
| 4 | 1 | 0.63 |
| 5 | 0 | 0.59 |
| 6 | 1 | 0.45 |
| 7 | 1 | 0.37 |
| 8 | 0 | 0.20 |
| 9 | 0 | 0.12 |
| 10 | 0 | 0.05 |
Set the threshold \(\tau_1\) = 0.95, calculate \({TPR}_1, {FPR}_1\)
Set the threshold \(\tau_2\) = 0.85, calculate \({TPR}_2, {FPR}_2\)
Set the threshold \(\tau_3\) = 0.72, calculate \({TPR}_3, {FPR}_3\)
…
…
Set the threshold \(\tau_n\) = 0.05, calculate \({TPR}_n, {FPR}_n\)
Now, we have ’n’ pairs of (TPR, FPR) for all ’n’ data points.
Plot the points on a graph to get the final ROC curve.
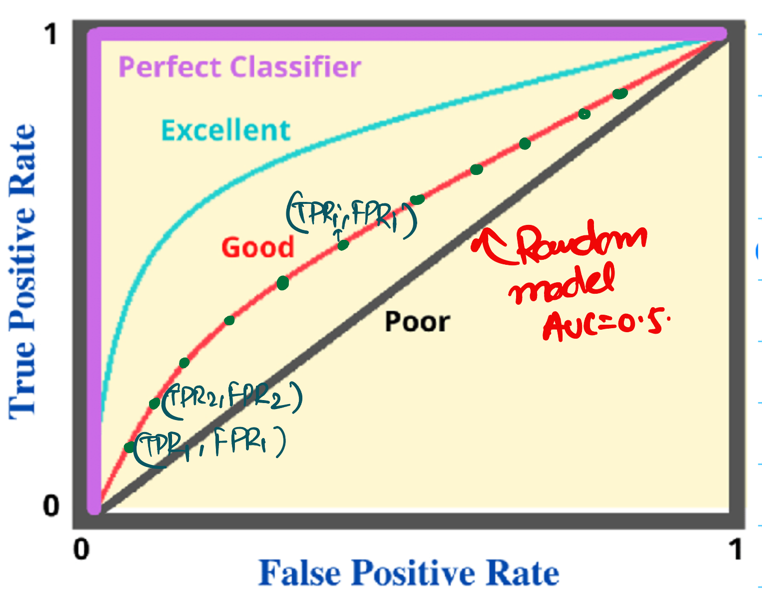
AU ROC = AUC = Area under the ROC curve = Area under the curve
Note:
Let’s understand this with the below fraud detection example.
Below is a dataset from a fraud detection system for N = 10,000 transactions.
Fraud = 100, NOT fraud = 9900
| Predicted Fraud | Predicted NOT Fraud | |
|---|---|---|
| Actual Fraud | 80 (TP) | 20 (FN) |
| Actual NOT Fraud | 220 (FP) | 9680 (TN) |
If we check the location of above (TPR, FPR) pair on the ROC curve, then we can see that it is
very close to the top-left corner.
This means that the model is very good at detecting fraudulent transactions, but that is NOT the case.
This is happening because of the imbalanced data, i.e, count of NOT fraud transactions is 99 times
of fraudulent transactions.
Let’s look at the Precision value:
We can see that the model has poor precision,i.e, only 26.7% of flagged transactions are actual frauds.
Unacceptable precision for a good fraud detection system.
Precision-Recall Curve:
It is used to evaluate the performance of a binary classifier model across various thresholds.
It is similar to the ROC curve, but it uses Precision instead of TPR on the Y-axis.
Plots Precision (Y-axis) against Recall (X-axis) for different classification thresholds.
Note: It is useful when the data is imbalanced.
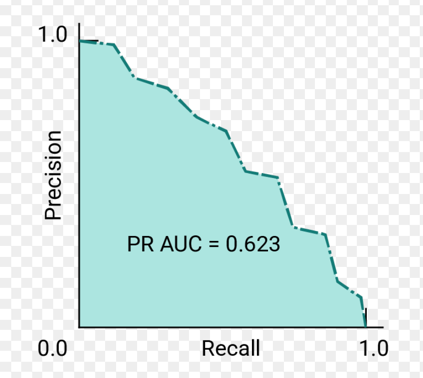
AU PRC = PR AUC = Area under Precision-Recall curve
Let’s revisit the fraud detection example discussed above to understand the utility of PR curve.
| Predicted Fraud | Predicted NOT Fraud | |
|---|---|---|
| Actual Fraud | 80 (TP) | 20 (FN) |
| Actual NOT Fraud | 220 (FP) | 9680 (TN) |
If we check the location of above (Precision, Recall) point on PRC curve, we will find that it is located near the
bottom right corner, i.e, the model performance is poor.
End of Section