Bagging

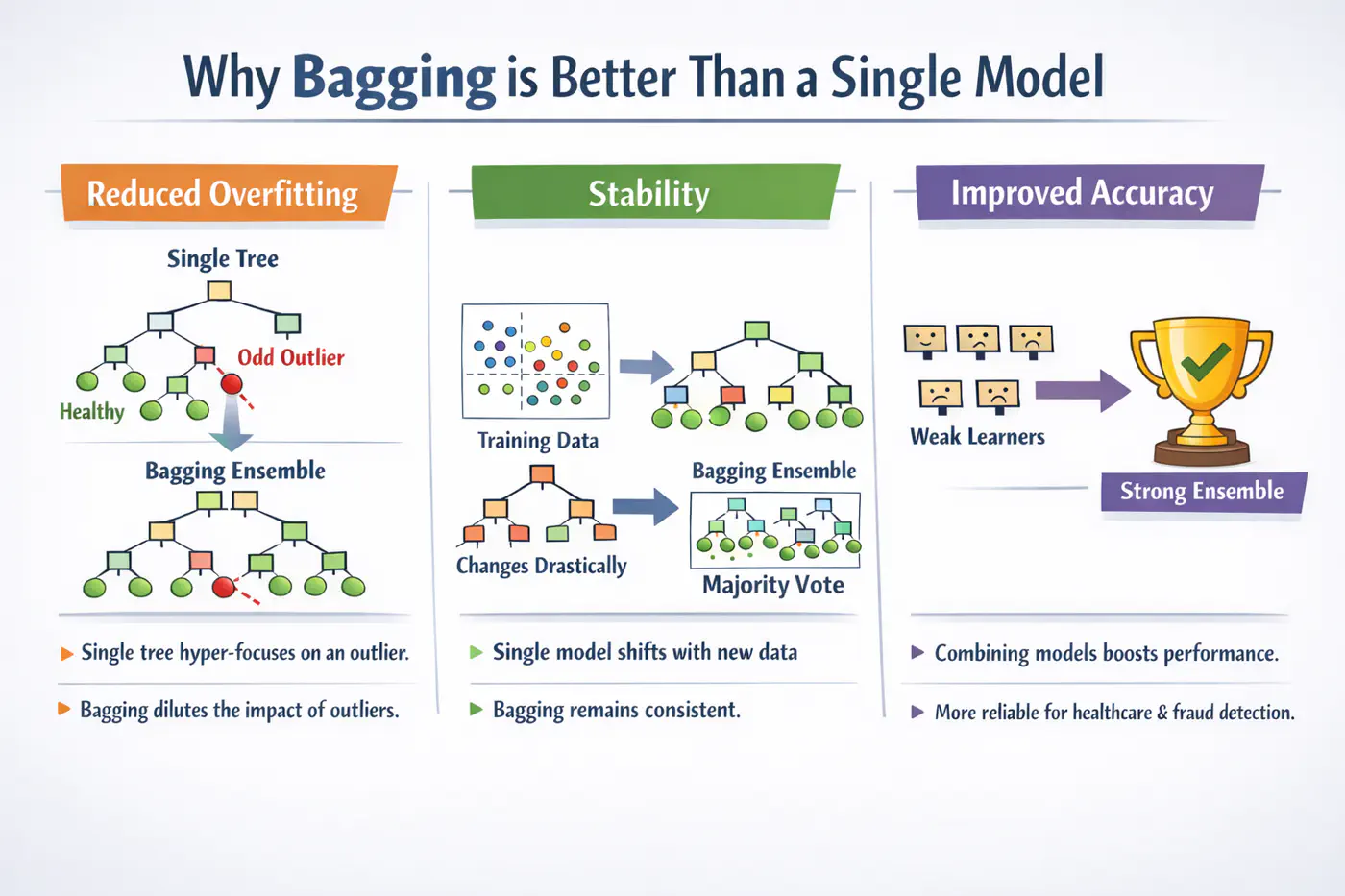
• A single decision tree is highly sensitive to the specific training dataset.
  Small changes, such as, a few different rows or the presence of an outlier, can lead to a completely different tree structure.

• Unpruned decision trees often grow until they perfectly classify the training set, essentially ‘memorizing’ noise and outliers, i.e, high variance, rather than finding general patterns.

Bagging = ‘Bootstrapped Aggregation’

Bagging 🎒is a parallel ensemble technique that reduces variance (without significantly increasing the bias) by training multiple versions of the same model on different random subsets of data and then combining their results.

Note: Bagging uses deep trees (overfit) and combines them to reduce variance.

Bootstrapping = ‘Without external help’

Given a training 🏃‍♂️set D of size ’n’, we create B new training sets D by sampling ’n’ observations from D ‘with replacement'.

💡Since, we are sampling ‘with replacement’, so, some data points may be picked multiple times, while others may not be picked at all.

• The probability that a specific observation is not selected in a bootstrap sample of size ’n’ is: \[\lim_{n \to \infty} \left(1 - \frac{1}{n}\right)^n = \frac{1}{e} \approx 0.368\]

🧐This means each tree is trained on roughly 63.2% of the unique data, while the remaining 36.8% (the Out-of-Bag or OOB set) can be used for cross validation.

⭐️Say we train ‘B’ models (base-learners), each with variance \(\sigma^2\) .

👉Average variance of ‘B’ models (trees) if all are independent:

👉Since, bootstrap samples are derived from the same dataset, the trees are correlated with some correlation coefficient ‘\(\rho\)'.

So, the true variance of bagged ensemble is:

• \(\rho\)= 0; independent models, most reduction in variance.
• \(\rho\)= 1; fully correlated models, no improvement in variance.
• 0<\(\rho\)<1; As correlation decreases, variance reduces .