Purity Metrics
2 minute read
Decision trees recursively partition the data based on feature values.
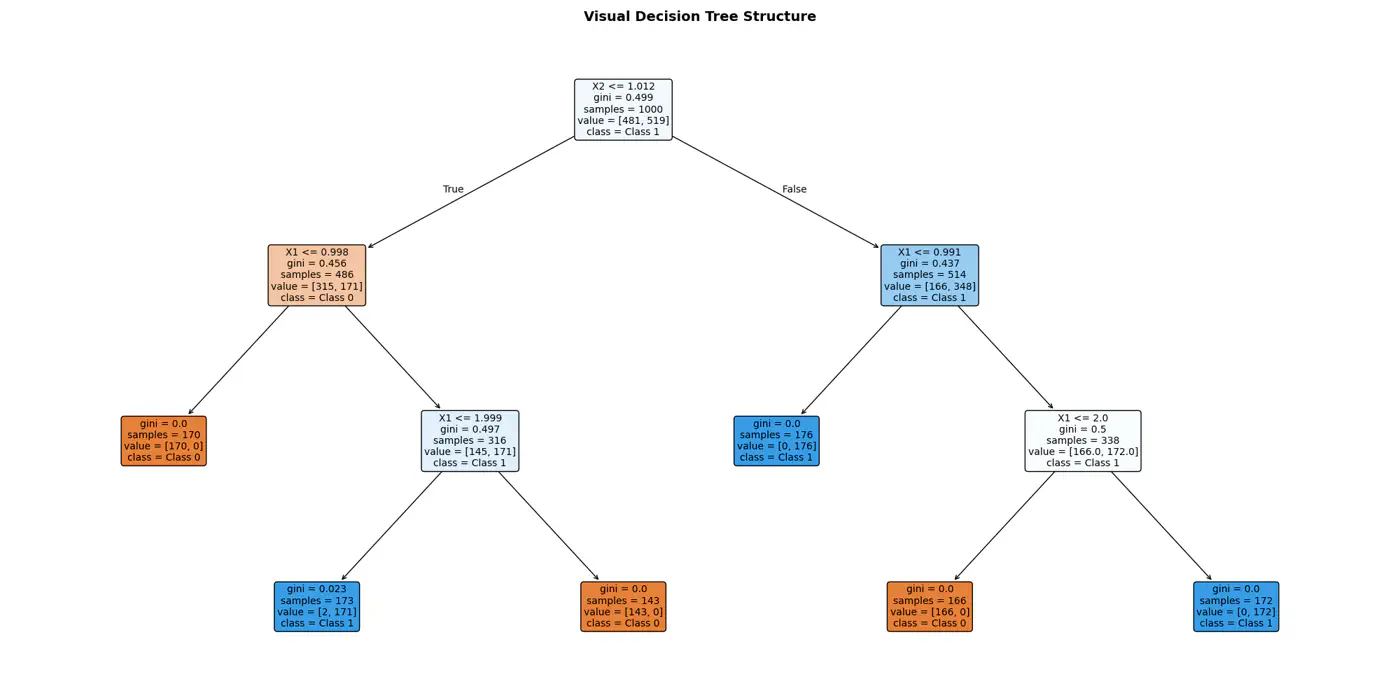
Pure Leaf 🍃 Node: Terminal node where every single data point belongs to the same class.
💡Zero Uncertainty.
The goal of a decision tree algorithm is to find the split that maximizes information gain, meaning it removes the most uncertainty from the data.
So, what is information gain ?
How do we reduce uncertainty ?
Let’s understand few terms first, before we understand information gain.
Measure ⏱ of uncertainty, randomness, or impurity in a data.
\[H(S)=-\sum _{i=1}^{n}p_{i}\log(p_{i})\]Binary Entropy:
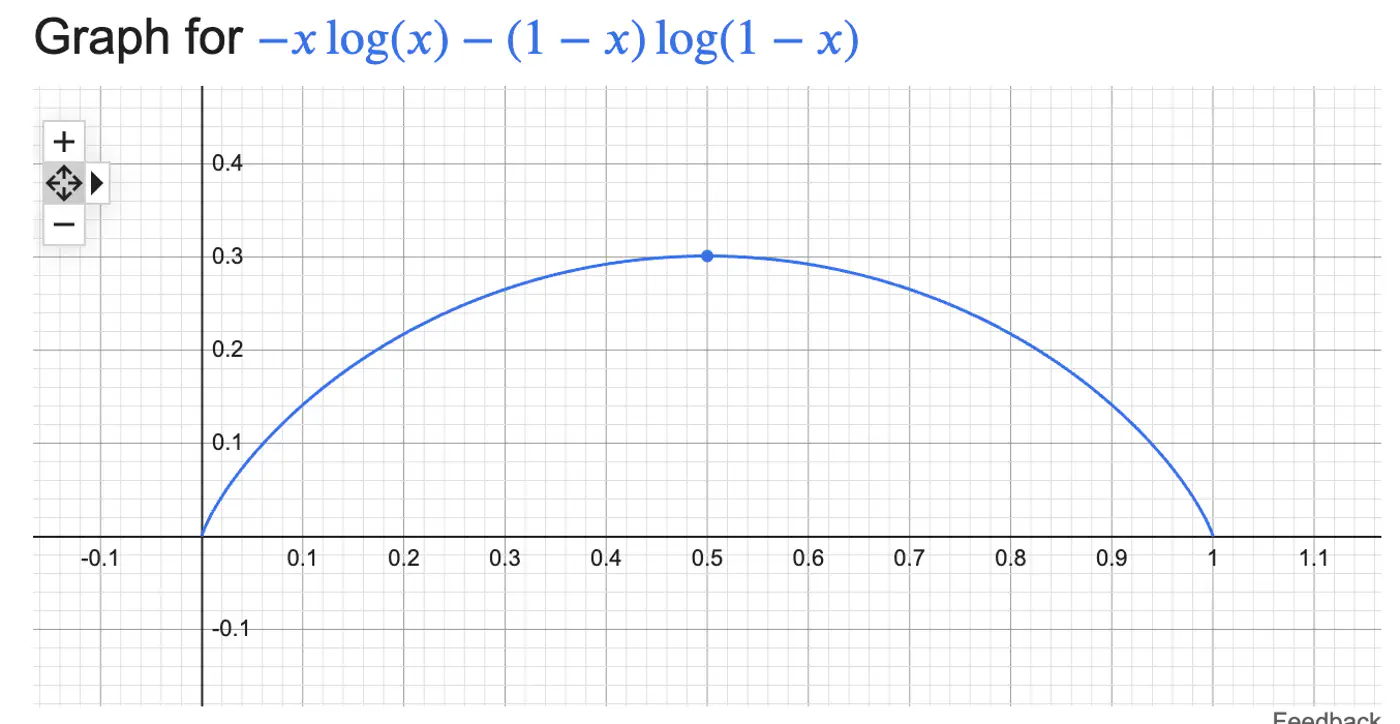
💡Entropy can also be viewed as the ‘average surprise'.
A highly certain event provides little information when it occurs (low surprise).
An unlikely event provides a lot of information (high surprise).

⭐️Measures ⏱ the reduction in entropy (uncertainty) achieved by splitting a dataset based on a specific attribute.
\[IG=Entropy(Parent)-\left[\frac{N_{left}}{N_{parent}}Entropy(Child_{left})+\frac{N_{right}}{N_{parent}}Entropy(Child_{right})\right] \]Note: The goal of a decision tree algorithm is to find the split that maximizes information gain, meaning it removes the most uncertainty from the data.
⭐️Measures ⏱ the probability of an element being incorrectly classified if it were randomly labeled according to the distribution of labels in a node.
\[Gini(S)=1-\sum_{i=1}^{n}(p_{i})^{2}\]- Range: 0 (Pure) - 0.5 (Maximum impurity)
Note: Gini is used in libraries like Scikit-Learn (as the default), because it avoids the computationally expensive 💰 log function.
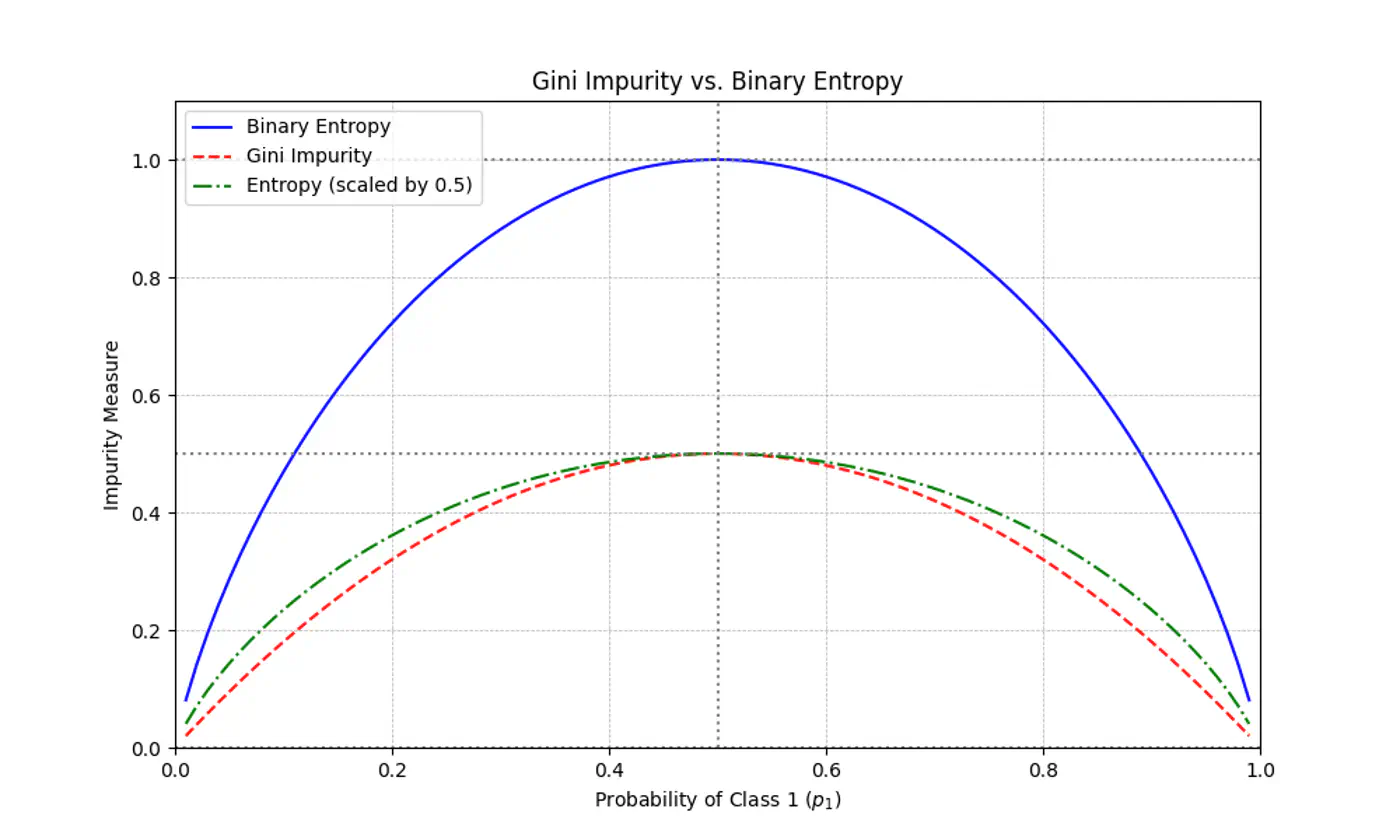
Gini Impurity is a first-order approximation of Entropy.
For most of the real-world cases, choosing one over the other results in the exact same tree structure or negligible differences in accuracy.
When we plot the two functions, they follow nearly identical shapes.
End of Section