Regularization
Regularization
2 minute read
Over-Fitting
⭐️Because trees🌲 are non-parametric and ‘greedy’💰, they will naturally try to grow 📈 until every leaf 🍃 is pure,
effectively memorizing noise and outliers rather than learning generalizable patterns.
Tree 🌲 Size
👉As the tree 🌲 grows, the amount of data in each subtree decreases 📉, leading to splits based on statistically insignificant samples.
Regularization Techniques
- Pre-Pruning ✂️ &
- Post-Pruning ✂️
Pre-Pruning ✂️
⭐️ ‘Early stopping’ heuristics (hyper-parameters).
- max_depth: Limits how many levels of ‘if else’ the tree can have; most common.
- min_samples_split: A node will only split, if it has at least ‘N’ samples; smooths the model (especially in regression), by ensuring predictions are based on an average of multiple points.
- max_leaf_nodes: Limiting the number of leaves reduces the overall complexity of the tree, making it simpler and less likely to memorize the training data’s noise.
- min_impurity_decrease: A split is only made if it reduces the impurity (Gini/MSE) by at least a certain threshold.
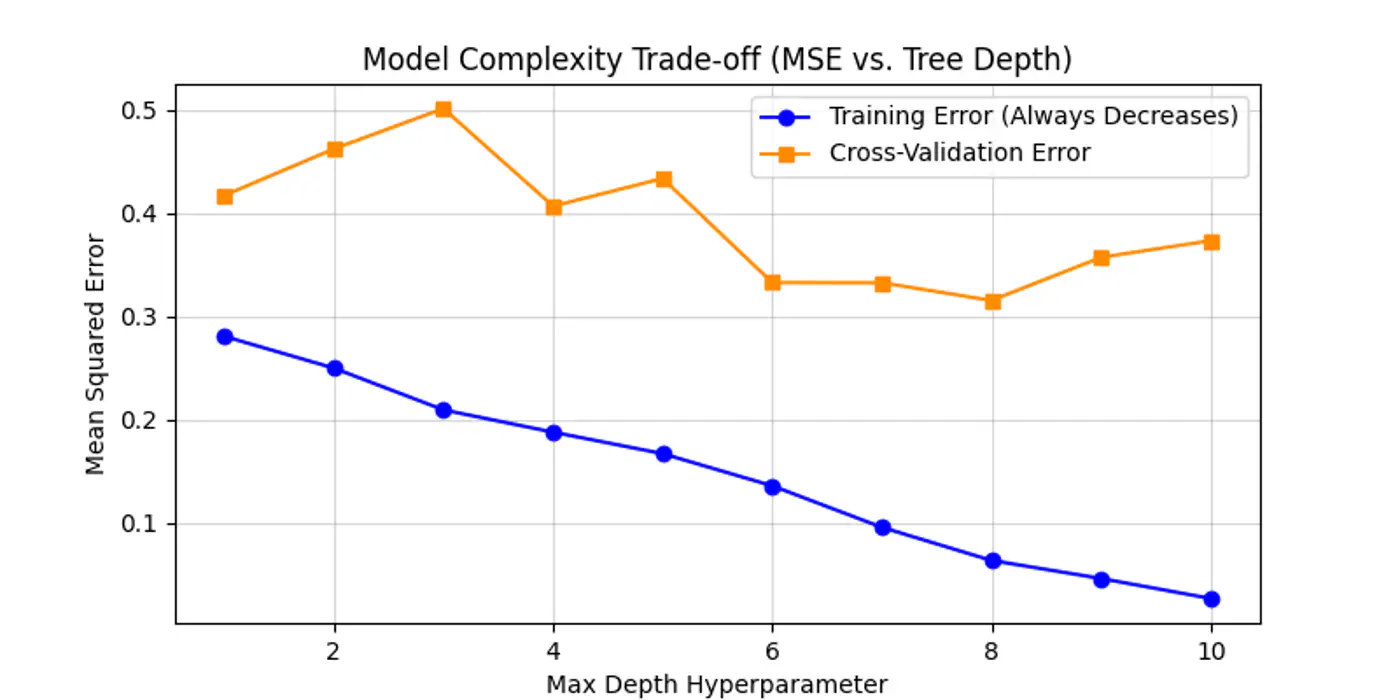
Max Depth Hyper Parameter Tuning
Below is an example for one of the hyper-parameter’s max_depth tuning.
As we can see below the cross-validation error decreases till depth=6 and after that reduction in error is not so significant.
Post-Pruning ✂️
Let the tree🌲 grow to its full depth (overfit) and then ‘collapse’ nodes that provide little predictive value.
Most common algorithm:
- Minimal Cost Complexity Pruning
Minimal Cost Complexity Pruning ✂️
💡Define a cost-complexity 💰 measure that penalizes the tree 🌲 for having too many leaves 🍃.
\[R_\alpha(T) = R(T) + \alpha |T|\]- R(T): total misclassification rate (or MSE) of the tree
- |T|: number of terminal nodes (leaves)
- \(\alpha\): complexity parameter (the ‘tax’ 💰 on complexity)
Logic:
- If \(\alpha\)=0, the tree is the original overfit tree.
- As \(\alpha\) increases 📈, the penalty for having many leaves grows 📈.
- To minimize the total cost 💰, the model is forced to prune branches that do not significantly reduce R(T).
- Use cross-validation to find the ‘sweet spot’ \(\alpha\) that minimizes validation error.
End of Section