XgBoost

⭐️An optimized and highly efficient implementation of gradient boosting.

👉 Widely used in competitive data science (like Kaggle) due to its speed and performance.

Note: Research project developed by Tianqi Chen during his doctoral studies at the University of Washington.

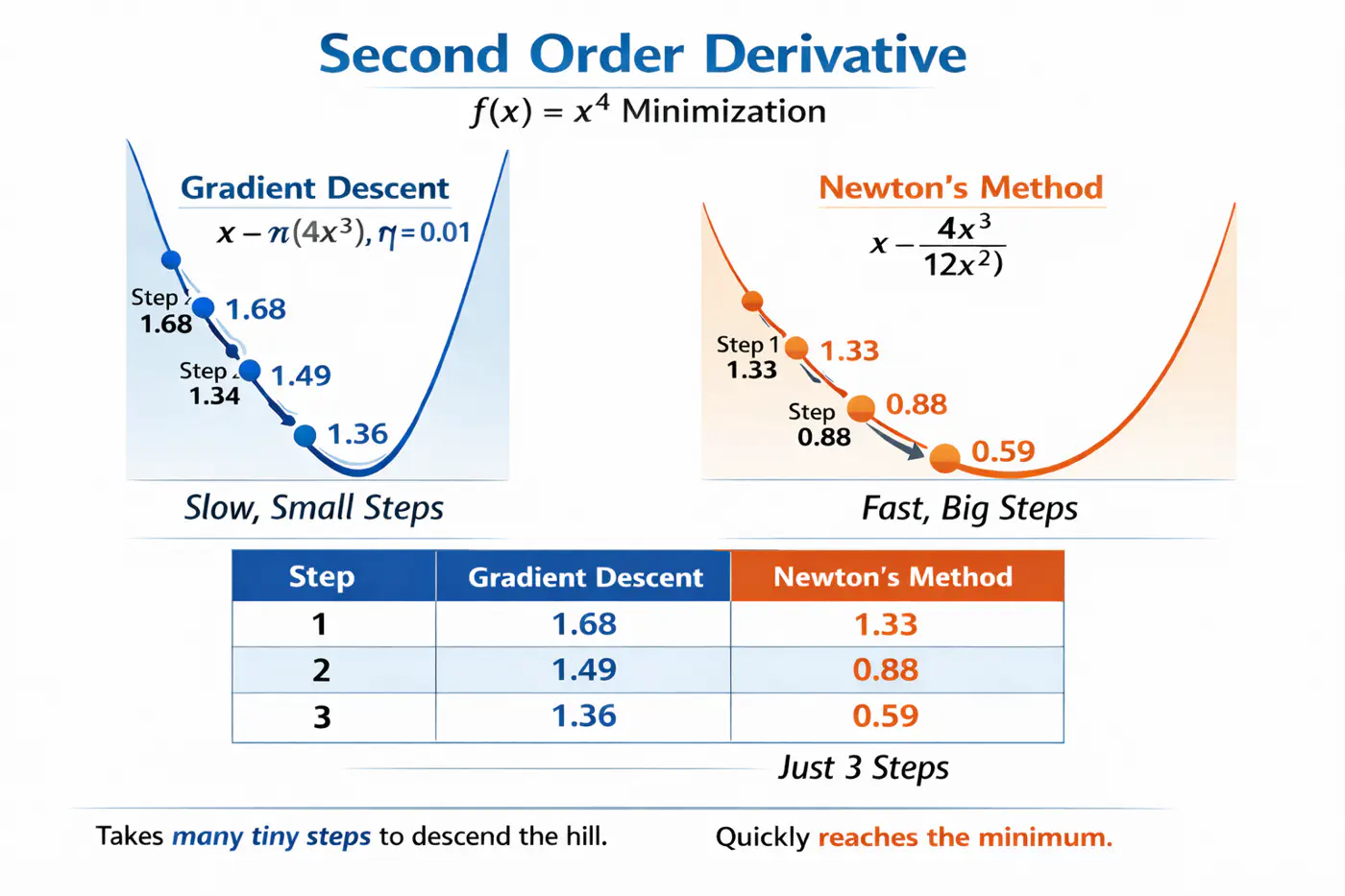
⭐️Uses second derivative (Hessian), i.e, curvature, in addition to first derivative (gradient) to optimize the objective function more quickly and accurately than GBDT.

Let’s understand this with the problem to minimize \(f(x) = x^4\), using:

• Gradient descent (uses only 1st order derivative, \(f'(x) = 4x^3\))

• Newton’s method (uses both 1st and 2nd order derivatives \(f''(x) = 12x^2\))

  

• Adds explicit regularization terms (L1/L2 on leaf weights and tree complexity) into the boosting objective, helping reduce over-fitting. \[ \text{Objective} = \underbrace{\sum_{i=1}^{n} L(y_i, \hat{y}_i)}_{\text{Training Loss}} + \underbrace{\gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T} w_j^2 + \alpha \sum_{j=1}^{T} |w_j|}_{\text{Regularization (The Tax)}} \]

💡Real-world data often contains many missing values or zero-entries (sparse data).

👉 XGBoost introduces a ‘default direction’ for each node.

➡️During training, it learns the best direction (left or right) for missing values to go, making it significantly faster and more robust when dealing with sparse or missing data.