Assumptions

Linear Regression works reliably only when certain key 🔑 assumptions about the data are met.

• Linearity
• Independence of Errors (No Auto-Correlation)
• Homoscedasticity (Equal Variance)
• Normality of Errors
• No Multicollinearity
• No Endogeneity (Target not correlated with the error term)

Relationship between features and target 🎯 is linear in parameters.

Note: Polynomial regression is linear regression.
\(y=w_0 +w_1x_1+w_2x_2^2 + w_3x_3^3\)

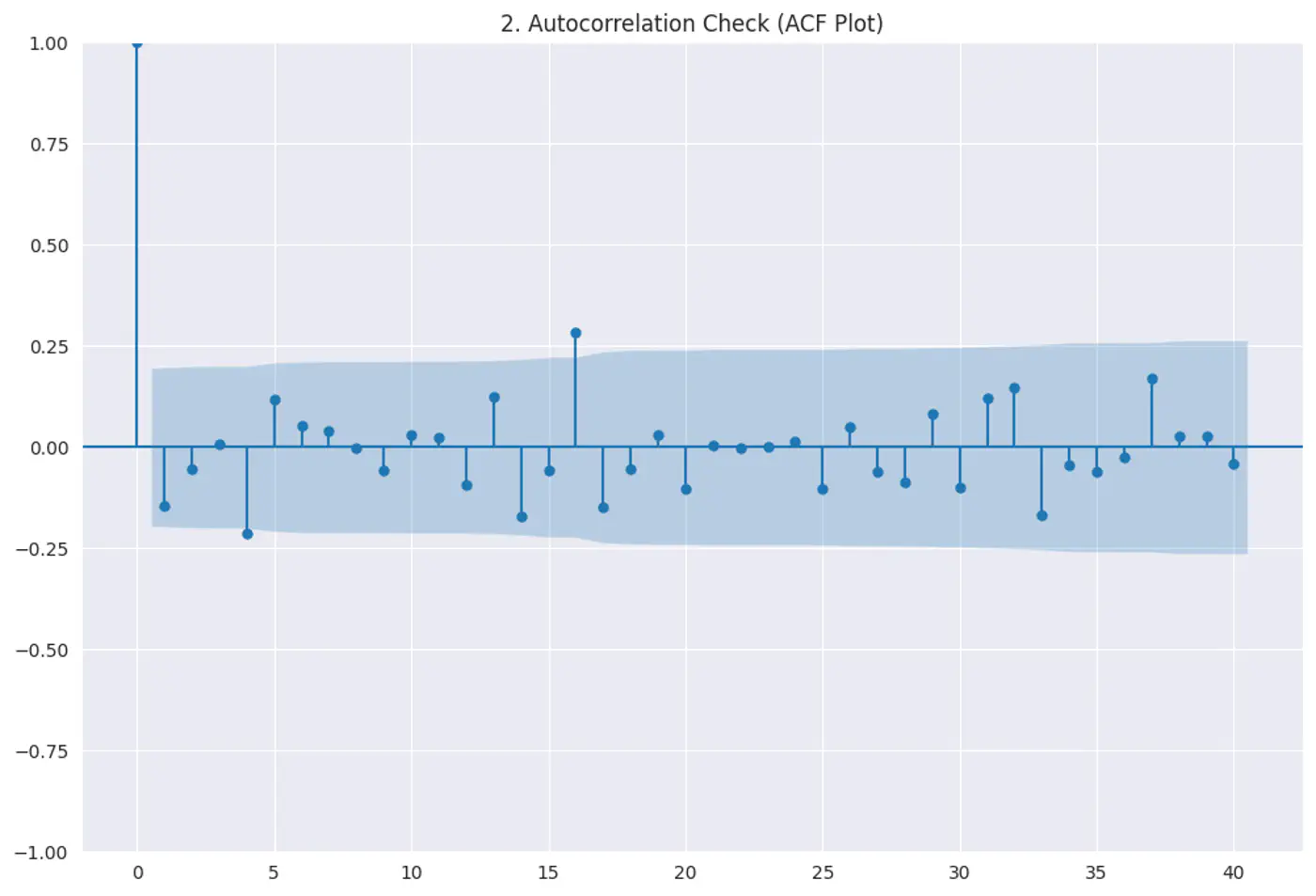
Residuals (errors) should not have a visible pattern or correlation with one another (most common in time-series ⏰ data).

Risk:
If errors are correlated, standard errors will be underestimated, making variables look ‘statistically significant’ when they are not.

Test:

• Durbin–Watson test

• Autocorrelation plots (ACF)

• Residuals vs time

  

Constant variance of errors; Var(ϵ|X)=σ

Risk:
Standard errors become biased, leading to unreliable hypothesis tests (t-tests, F-tests).

Test:

• Breusch–Pagan test
• White test

Fix:

• Log transform
• Weighted Least Squares(WLS)

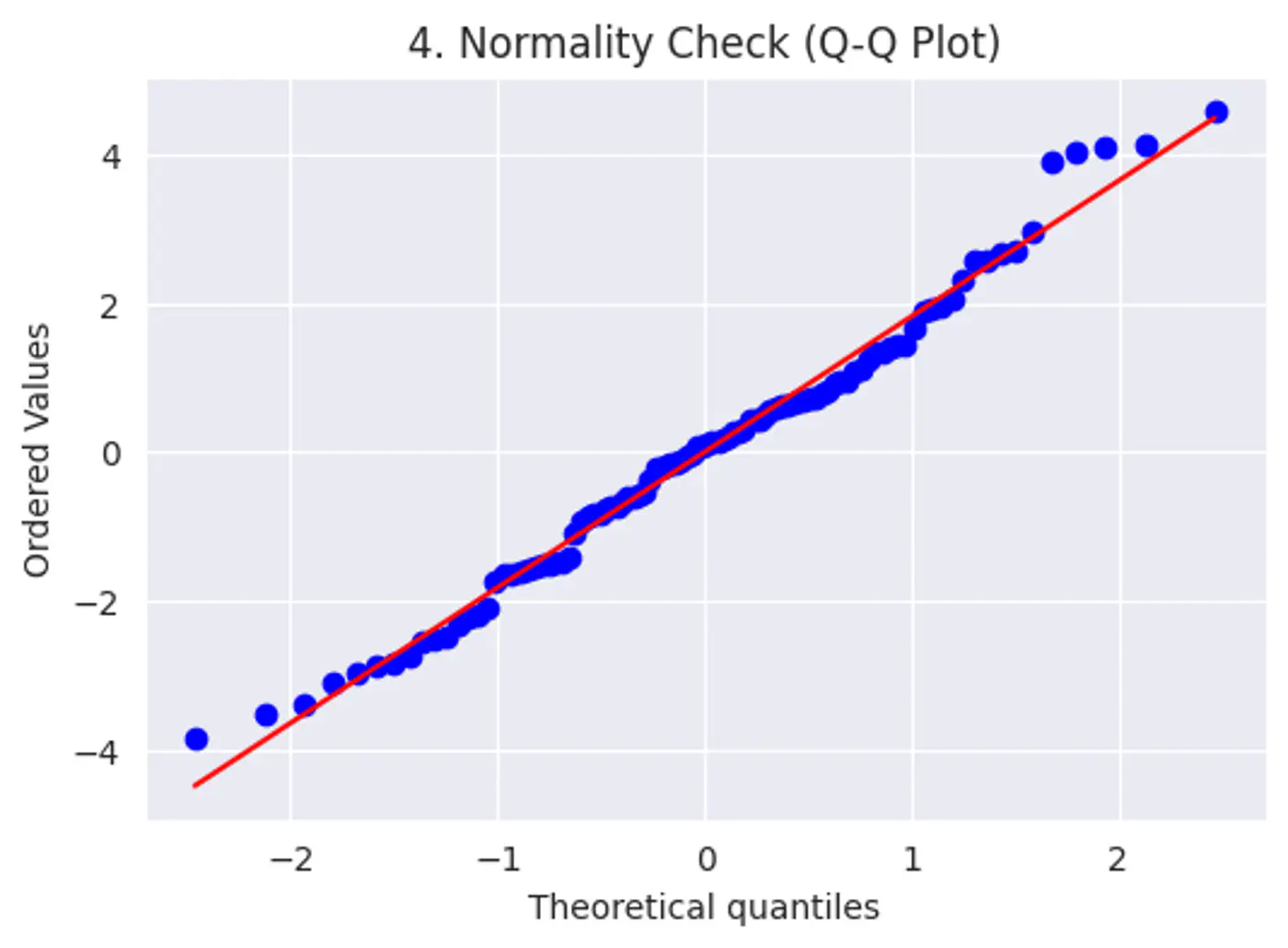
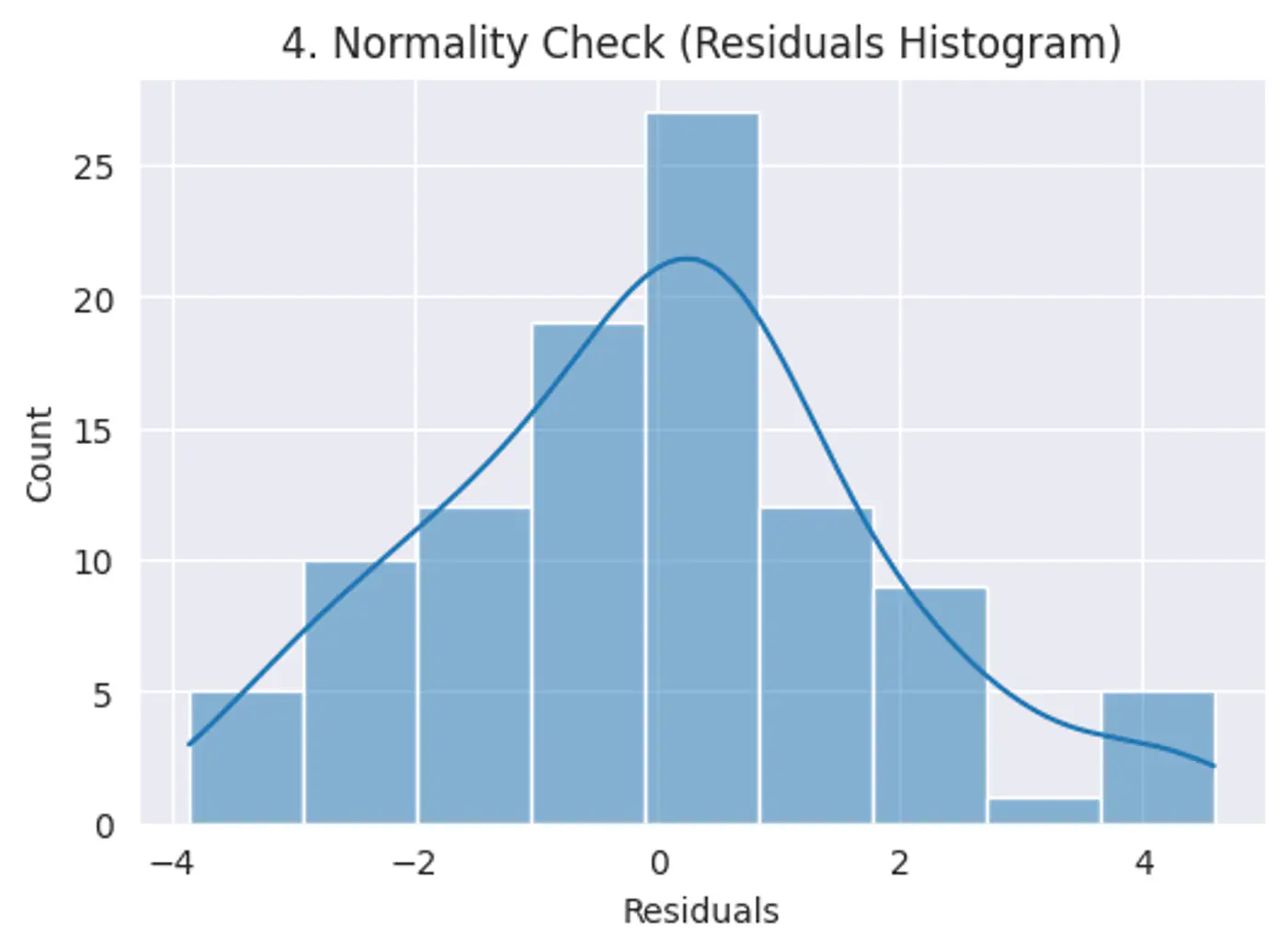
Error terms should follow a normal distribution; (Required for small datasets.)

Note: Because of Central Limit Theorem, with a large enough sample size, this becomes less critical for estimation.

Risk: Hypothesis testing (calculating p-values and confidence intervals), we assume the error terms follow a normal distribution.

Test:

• Q-Q plot

• Shapiro-Wilk Test

  

  

Features should not be highly correlated with each other.

Risk:

• High correlation makes it difficult to determine the unique, individual impact of each feature. This leads to high variance in model parameter estimates, small changes in data cause large swings in parameters.
• Model interpretability issues.

Test:

• Variance Inflation Factor(VIF)VIF > 5 → concern, VIF > 10 → serious issue

Fix:

• PCA
• Remove redundant features

Error term must be uncorrelated with the features; E[ϵ|X] = 0

Risk:

• Parameters will be biased and inconsistent.

Test:

• Hausman Test
• Durbin-Wu-Hausman (DWH) Test

Fix:

• Controlled experiments.