Bias Variance Tradeoff
2 minute read
Mean Squared Error (MSE) = \(\frac{1}{n} \sum_{i=1}^n (y_i - \hat{y_i})^2\)
Total Error = Bias^2 + Variance + Irreducible Error
- Bias = Systematic Error
- Bias measures how far the average prediction of a model is from the true value.
- Variance = Sensitivity to Data
- Variance measures how much the predictions of a model vary for different training datasets.
- Irreducible Error = Sensor noise, Human randomness
- Inherent uncertainty in the data generation process itself and cannot be reduced by any model.
Systematic error from overly simplistic assumptions or strong opinion in the model.
e.g. House prices = Rs. 10,000 * Area (sq. ft).
Note: This is over simplified view, because it ignores, amenities, location, age, etc.
Error from sensitivity to small fluctuations in the data.
e.g. Deep neural network trained on a small dataset.
Note: Memorizes everything, including noise.
Say a house in XYZ street was sold for very low price .
Reason: Distress selling (outlier), or incorrect entry (noise).
Note: Model will make wrong(lower) price predictions for all houses in XYZ street.
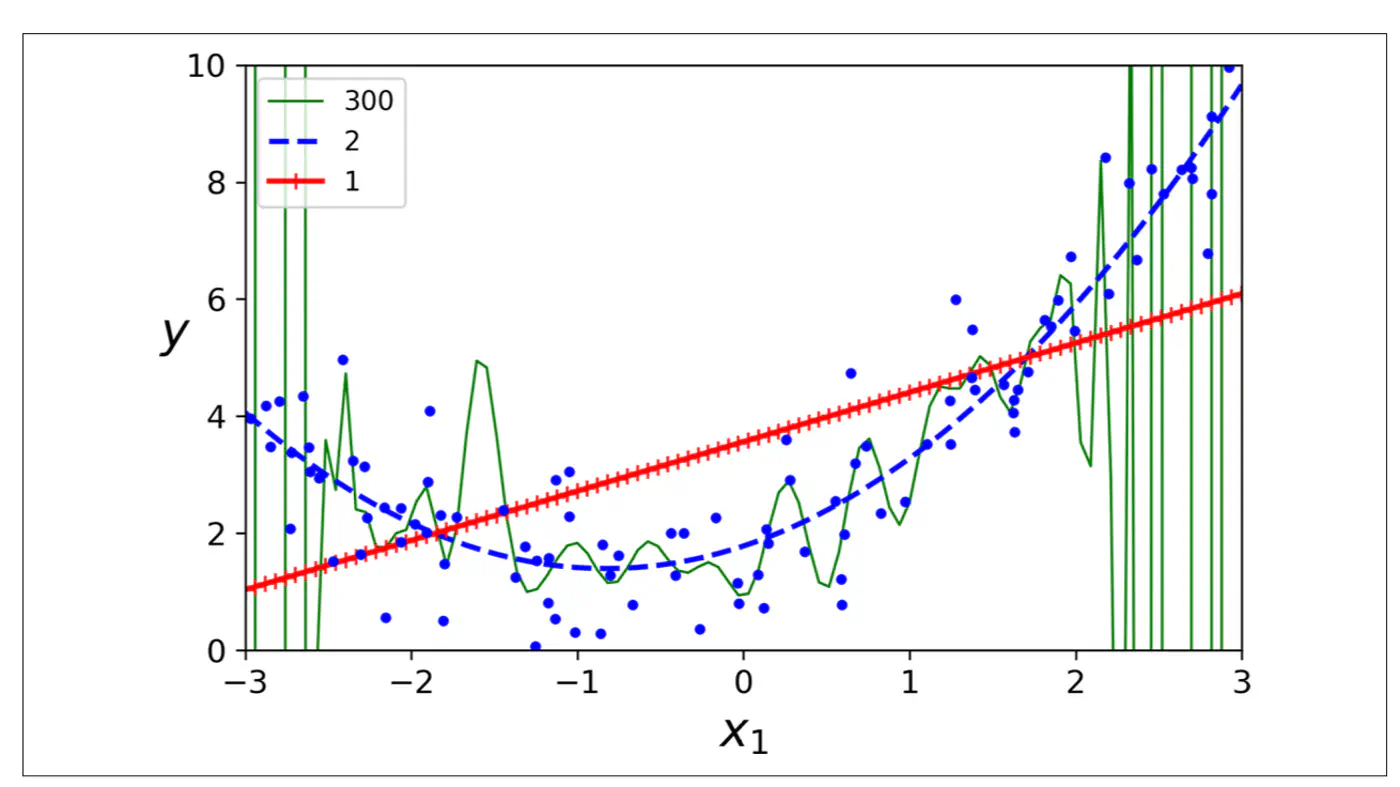
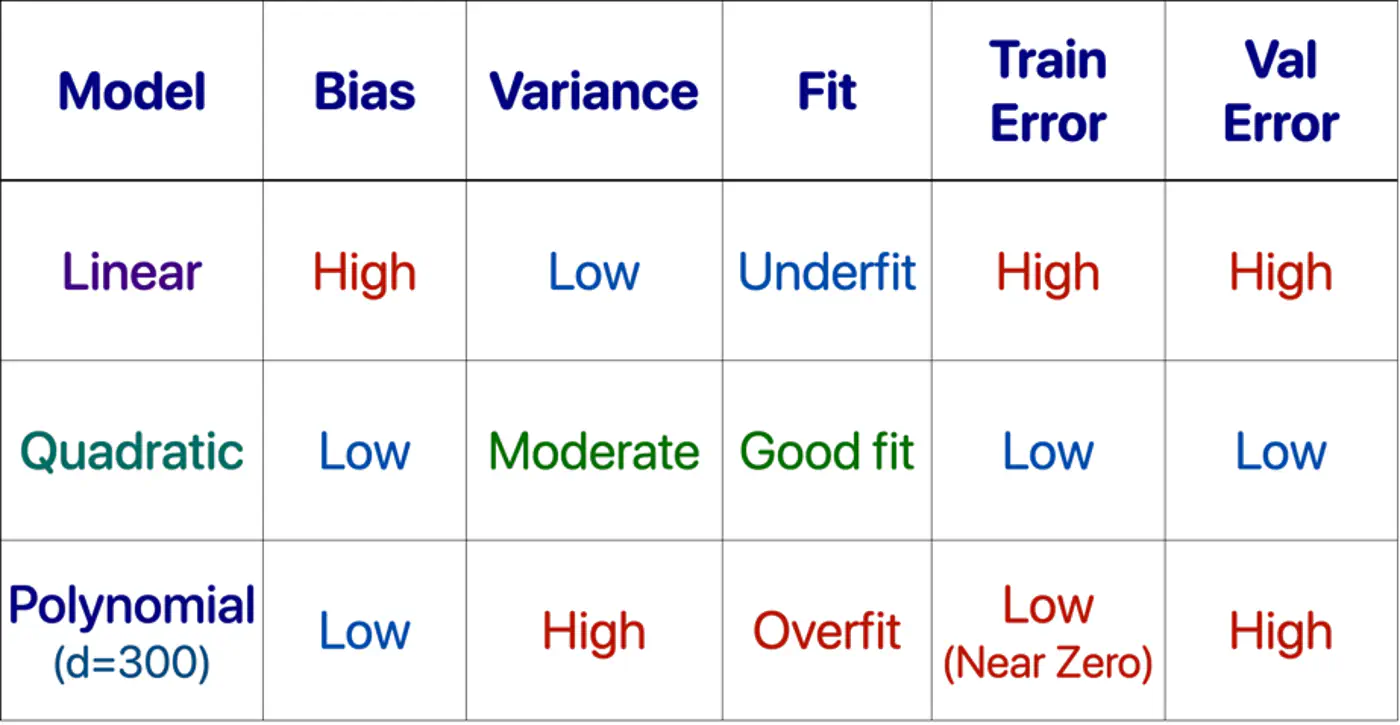
Goal is to minimize total error.
Find a sweet-spot balance between Bias and Variance.
A good model ‘generalizes’ well, i.e.,
- Is not too simple or has a strong opinion.
- Does not memorize everything in the data, including noise.
- Make model more complex.
- Add more features, add polynomial features.
- Decrease Regularization.
- Train longer, the model has not yet converged.
- Add more data (most effective).
- Harder to memorize 1 million examples than 100.
- Use data augmentation, if getting more data is difficult.
- Increase Regularization.
- Early stopping , prevents memorization .
- Dropout (DL), randomly kill neurons, prevents co-adaptation.
- Use Ensembles.
- Averaging reduces variance.
Note: Co-adaptation refers to a phenomenon where neurons in a neural network become highly dependent on each other to detect features, rather than learning independently.
End of Section