Convex Function
Convex Function
less than a minute
Convexity
Refers to a property of a function where a line segment connecting any two points on its graph lies above or on the graph itself.
A convex function is curved upwards.
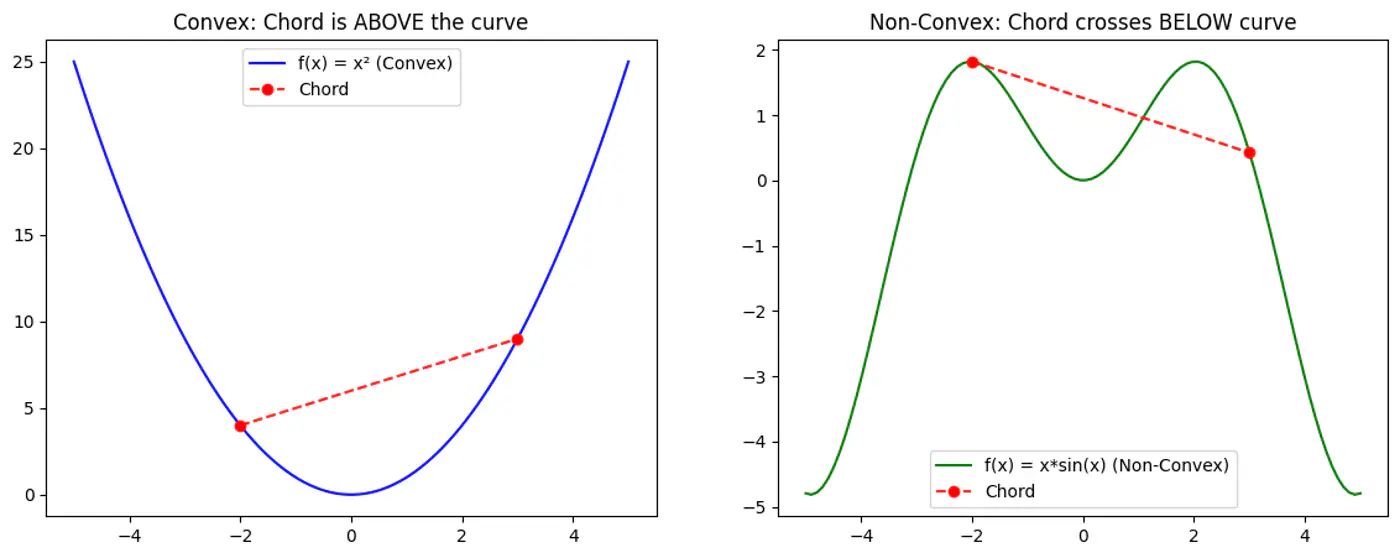
Is MSE Cost function Convex ? YES ✅
MSE cost function J(w) is convex because its Hessian (H) is always positive semi definite.
\[\nabla J(\mathbf{w})=\frac{1}{n}\mathbf{X}^{T}(\mathbf{Xw}-\mathbf{y})\]\[\mathbf{H}=\frac{\partial (\nabla J(\mathbf{w}))}{\partial \mathbf{w}^{T}}=\frac{1}{n}\mathbf{X}^{T}\mathbf{X}\]\[\therefore \mathbf{H} = \nabla^2J(w) = \frac{1}{n} \mathbf{X}^{T}\mathbf{X}\]
MSE: Positive Semi Definite (Proof)
A matrix H is positive semi-definite if and only if for any non-zero vector ‘z’, the quadratic form \(z^THz \ge 0\).
For the Hessian of J(w),
\[ z^THz = z^T(\frac{1}{n}X^TX)z = \frac{1}{n}(Xz)^T(Xz) \]\((Xz)^T(Xz) = \lVert Xz \rVert^2\) = squared L2 norm (magnitude) of the vector
Note: The squared norm of any real-valued vector is always \(\ge 0\).
End of Section