Meaning of 'Linear'
2 minute read
Equation of a line is of the form \(y = mx + c\).
To represent a line in 2D space, we need 2 things:
- m = slope or direction of the line
- c = y-intercept or distance from the origin
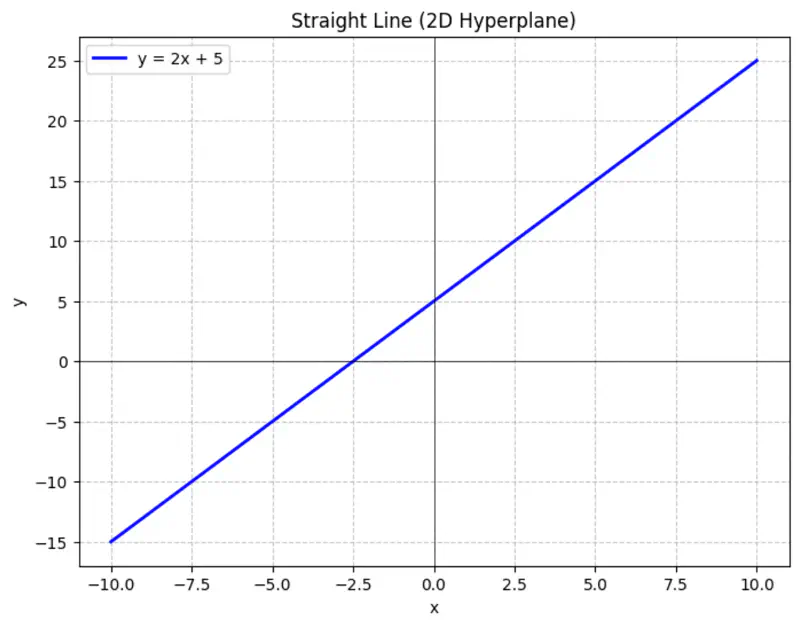
Similarly,
A hyperplane is a lower (d-1) dimensional sub-space that divides a d-dimensional space into 2 distinct parts.
Equation of a hyperplane:
Here, ‘y’ is expressed as a linear combination of parameters - \( w_0, w_1, w_2, \dots, w_n \)
Hence - Linear means the model is ‘linear’ with respect to its parameters NOT the variables.
Read more about Hyperplane
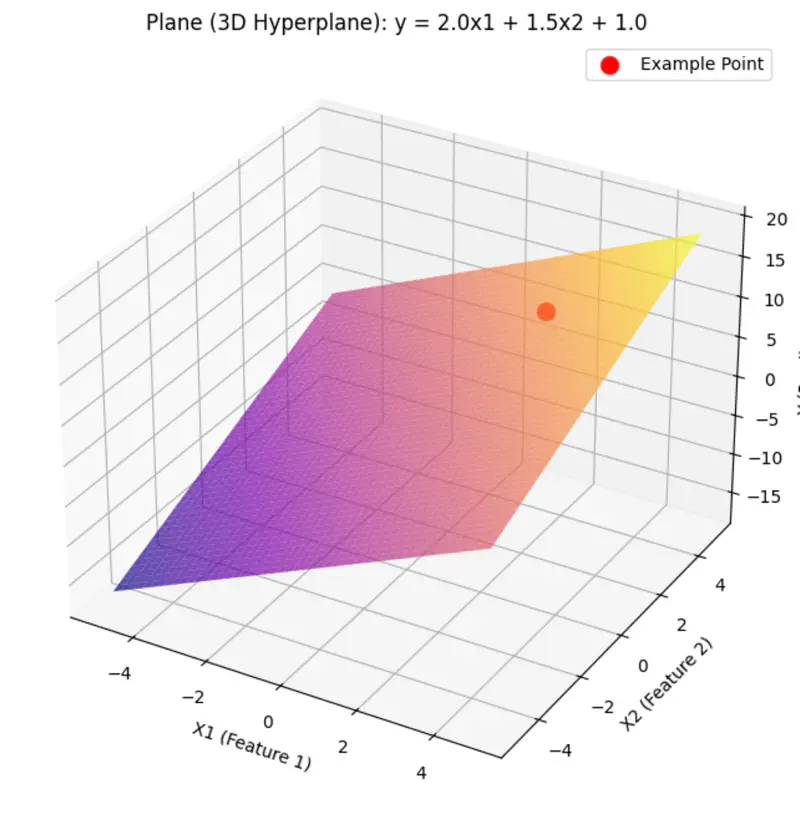
can be rewritten as:
\[y = w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_0\]where, \(x_3 = x_1^2 ~ and ~ x_4 = x_2^3 \)
\(x_3 ~ and ~ x_4 \) are just 2 new (polynomial) variables.
And, ‘y’ is still a linear combination of parameters: \(w_0, w_1, \dots w_4\)
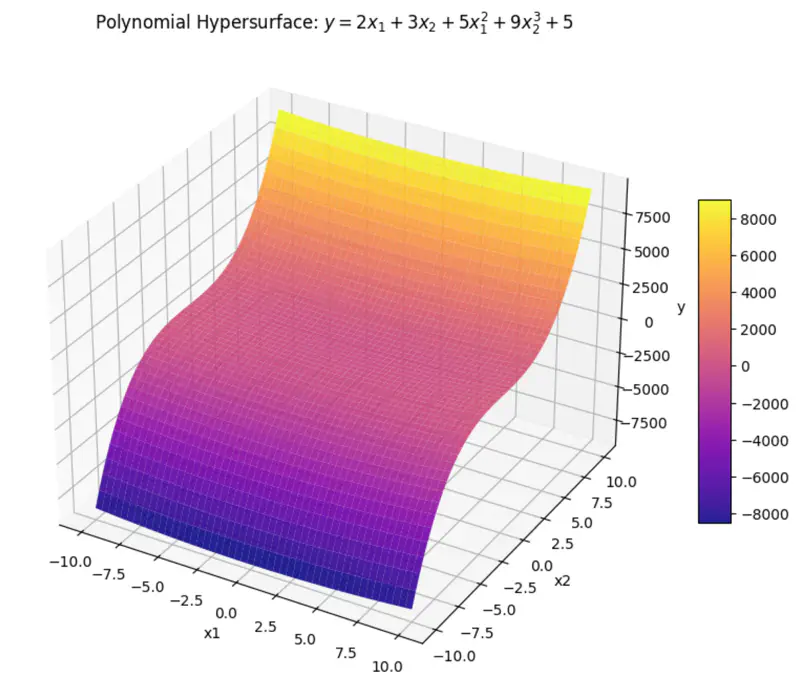
can be rewritten as:
\[y = w_1x_1 + w_2x_2 + w_0\]where, \(x_1 = log(x) ~ and ~ x_2 = \sqrt{x} \)
\(x_1 ~ and ~ x_2 \) are are transformations of variable \(x\).
And, ‘y’ is still a linear combination of parameters: \(w_0, w_1, ~and~ w_2\)
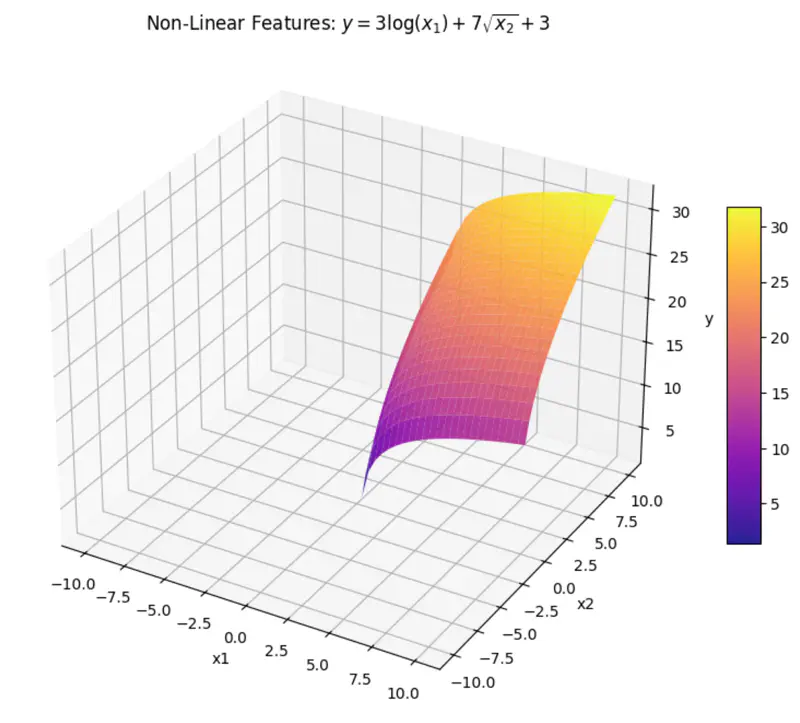
Even if we take log, we get:
\[log(y) = w_1log(x_1) + w_2log(x_2) + log(w_0)\]here, \(log(w_0) \) parameter is NOT linear.
End of Section