Regularization
Regularization in Logistic Regression
less than a minute
What happens to the weights of Logistic Regression if the data is perfectly linearly separable?
The weights 🏋️♀️ will tend towards infinity, preventing a stable solution.
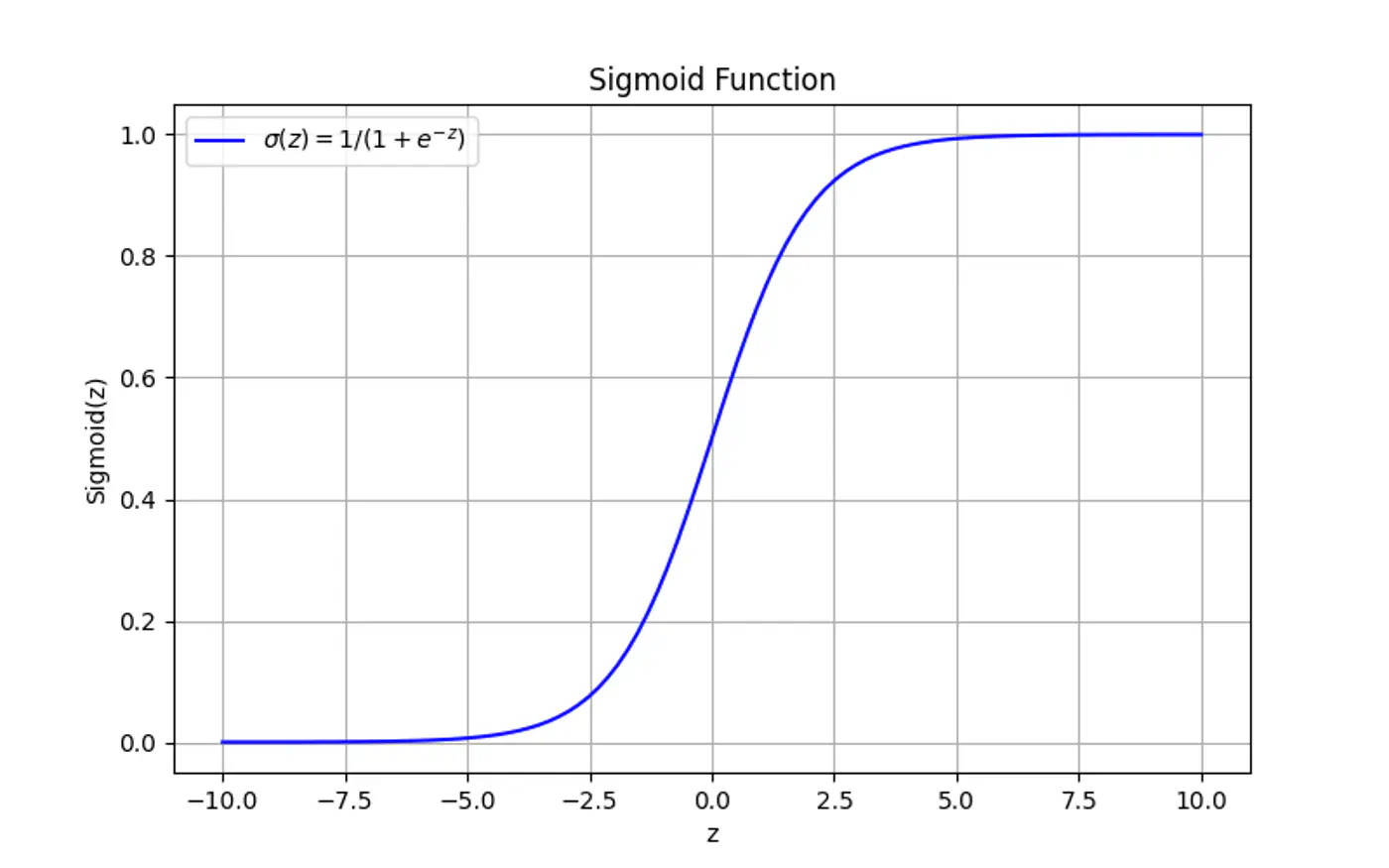
The model tries to make probabilities exactly 0 or 1, but the sigmoid function never reaches these limits, leading to extreme weights 🏋️♀️ to push probabilities near the extremes.
Distance of Point: \(z = \mathbf{w^Tx} + w_0\)
Prediction: \(\hat{y} = \sigma(z) = \frac{1}{1 + e^{-z}}\)
Log loss: \(-[y_ilog(\hat{y_i}) + (1-y_i)log(1-\hat{y_i})] \)
Why is it a problem ?
Overfitting:
Model becomes perfectly accurate on training 🏃♂️data but fails to generalize, performing poorly on unseen data.
Model becomes perfectly accurate on training 🏃♂️data but fails to generalize, performing poorly on unseen data.
Solution 🦉
Regularization:
Adds a penalty term to the loss function, discouraging weights 🏋️♀️ from becoming too large.
Adds a penalty term to the loss function, discouraging weights 🏋️♀️ from becoming too large.
L1 Regularization
\[
\begin{align*}
\underset{w}{\mathrm{min}}\ J_{reg}(w) = \underset{w}{\mathrm{min}}\
& \underbrace{- \sum_{i=1}^n [y_i\log(\hat{y_i}) + (1-y_i)\log(1-\hat{y_i})]}_{\text{Log Loss}} \\
& \underbrace{+ \lambda_1 \sum_{j=1}^n |w_j|}_{\text{L1 Regularization}} \\
\end{align*}
\]
L2 Regularization
\[
\begin{align*}
\underset{w}{\mathrm{min}}\ J_{reg}(w) = \underset{w}{\mathrm{min}}\
& \underbrace{- \sum_{i=1}^n [y_i\log(\hat{y_i}) + (1-y_i)\log(1-\hat{y_i})]}_{\text{Log Loss}} \\
& \underbrace{+ \lambda_2 \sum_{j=1}^n w_j^2}_{\text{L2 Regularization}} \\
\end{align*}
\]
End of Section