Naive Bayes Example
Naive Bayes Example
2 minute read
Naive Bayes
⭐️Simple, fast, and highly effective probabilistic machine learning classifier based on Bayes’ theorem.
\[\log(P(y| W)) \propto \sum_{i=1}^d \log(P(w_i|y)) + \log(P(y))\]\[P(w_{i}|y)=\frac{count(w_{i},y)+\alpha }{count(y)+\alpha \cdot |V|}\]Email Classification Problem
Let’s solve an email classification problem, below we have list of emails (tokenized) and labelled as Spam/Not Spam for training.
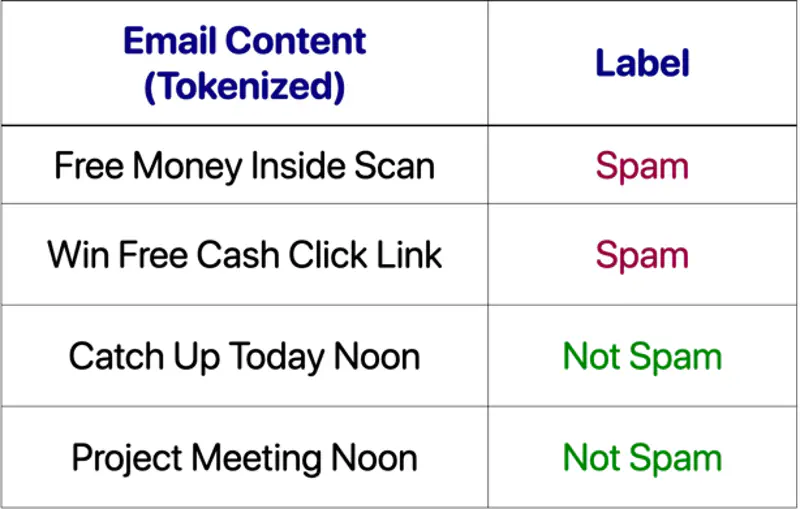
Training Phase
🏛️Class Priors:
- P(Spam) = 2/4 =0.5
- P(Not Spam) = 2/4 = 0.5
📕 Vocabulary = { Free, Money, Inside, Scan, Win, Cash, Click, Link, Catch, Up Today, Noon, Project, Meeting }
- |V| = Total unique word count = 14
🧮 Class count:
- count(Spam) = 9
- count(Not Spam) = 7
✅ Laplace smoothing: \(\alpha = 1\)
Likelihood of 'free'
\[P(w_{i}|y)=\frac{count(w_{i},y)+\alpha }{count(y)+\alpha \cdot |V|}\]
- P(‘free’| Spam) = \(\frac{2+1}{9+14} = \frac{3}{23} = 0.13\)
- P(‘free’| Not Spam) = \(\frac{0+1}{7+14} = \frac{1}{21} = 0.047\)
Inference Time
👉Say a new email 📧 arrives - “Free money today”; lets classify it as Spam/Not Spam.
Spam:
- P(‘free’| Spam) = \(\frac{2+1}{9+14} = \frac{3}{23} = 0.13\)
- P(‘money’| Spam) = \(\frac{1+1}{9+14} = \frac{2}{23} = 0.087\)
- P(‘today’| Spam) = \(\frac{0+1}{9+14} = \frac{1}{23} = 0.043\)
Not Spam:
- P(‘free’| Not Spam) = \(\frac{0+1}{7+14} = \frac{1}{21} = 0.047\)
- P(‘money’| Not Spam) = \(\frac{0+1}{7+14} = \frac{1}{21} = 0.047\)
- P(‘today’| Not Spam) = \(\frac{1+1}{7+14} = \frac{2}{21} = 0.095\)
Final Score 🏏
\[\log(P(y| W)) \propto \sum_{i=1}^d \log(P(w_i|y)) + \log(P(y))\]
- Score(Spam) = log(P(Spam)) + log(P(‘free’|S)) + log(P(‘money’|S)) + log(P(‘today’|S))
= log(0.5) + log(0.13) + log(0.087) + log(0.043) = -0.301 -0.886 -1.06 -1.366 = -3.614 - Score(Not Spam) = log(P(Not Spam)) + log(P(‘free’|NS)) + log(P(‘money’|NS)) + log(P(‘today’|NS))
= log(0.5) + log(0.047) + log(0.047) + log(0.095) = -0.301 -1.328 -1.328 -1.022 = -3.979
👉Since, Score(Spam) (-3.614 )> Score(Not Spam) (-3.979) , the model chooses ‘Spam’ as the label for the email.
End of Section