Hard Margin SVM

• Data is perfectly linearly separable, i.e, there must exist a hyperplane that can perfectly separate the data into two distinct classes without any misclassification.

• No noise or outliers that fall within the margin or on the wrong side of the decision boundary. Note: Even a single outlier can prevent the algorithm from finding a valid solution or drastically affect the boundary’s position, leading to poor generalization.

  

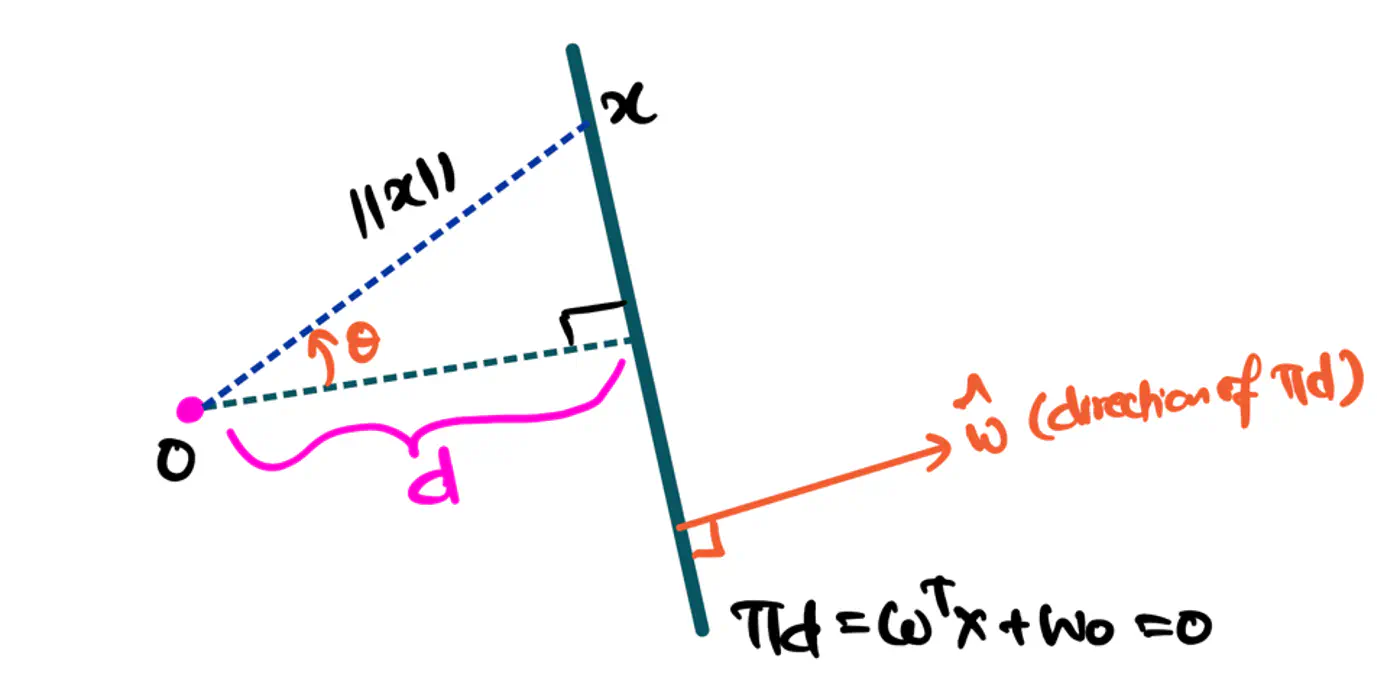
• 🐎 Distance(signed) of a hyperplane from origin = \(\frac{-w_0}{\|w\|}\)
• 🦣 Margin width = distance(\(\pi^+, \pi^-\))
• = \(\frac{1-w_0 - (-1 -w_0)}{\|w\|}\) = \(\frac{1-\cancel{w_0} + 1 + \cancel{w_0})}{\|w\|}\)
• distance(\(\pi^+, \pi^-\)) = \(\frac{2}{\|w\|}\)

Figure: Distance of Hyperplane from Origin

Read more about Hyperplane

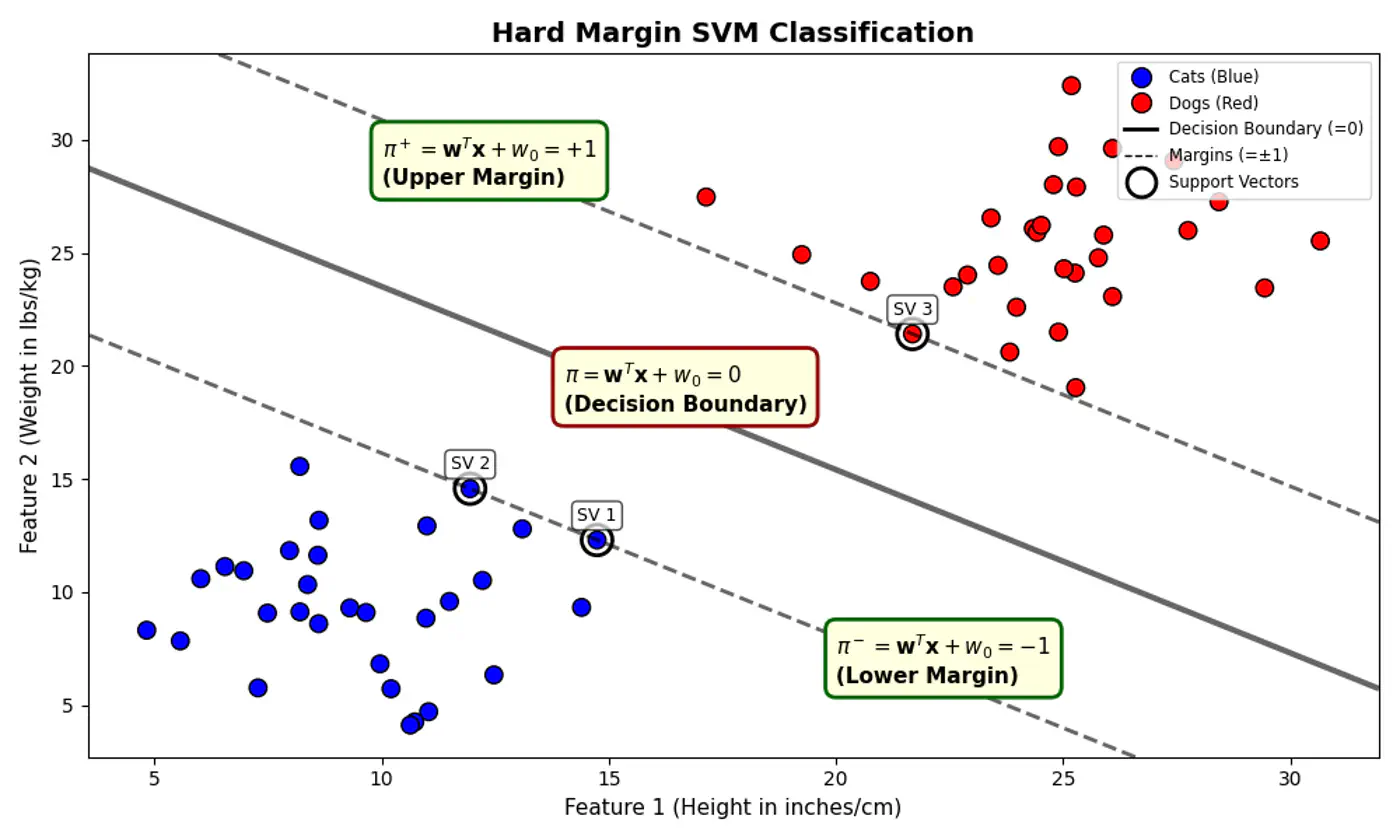
• Separating hyperplane \(\pi\) is exactly equidistant from \(\pi^+\) and \(\pi^-\).
• We want to maximize the margin between +ve(🐶) and -ve (😸) points.

👉Combining above two constraints:

such that, \(y_i.(w^Tx_i + w_0) \ge 1\)

👉To maximize the margin, we must minimize \(\|w\|\).
Since, distance(\(\pi^+, \pi^-\)) = \(\frac{2}{\|w\|}\)

such that, \(y_i.(w^Tx_i + w_0) \ge 1 ~ \forall i = 1,2,\dots, n\)

Note: Hard margin SVM will not work if the data has a single outlier or slight overlap.