Soft Margin SVM
2 minute read
💡Imagine the margin is a fence 🌉.
Hard Margin: fence is made of steel.
Nothing can cross it.Soft Margin: fence is made of rubber(porous).
Some points can ‘push’ into the margin or even cross over to the wrong side, but we charge them a penalty 💵 for doing so.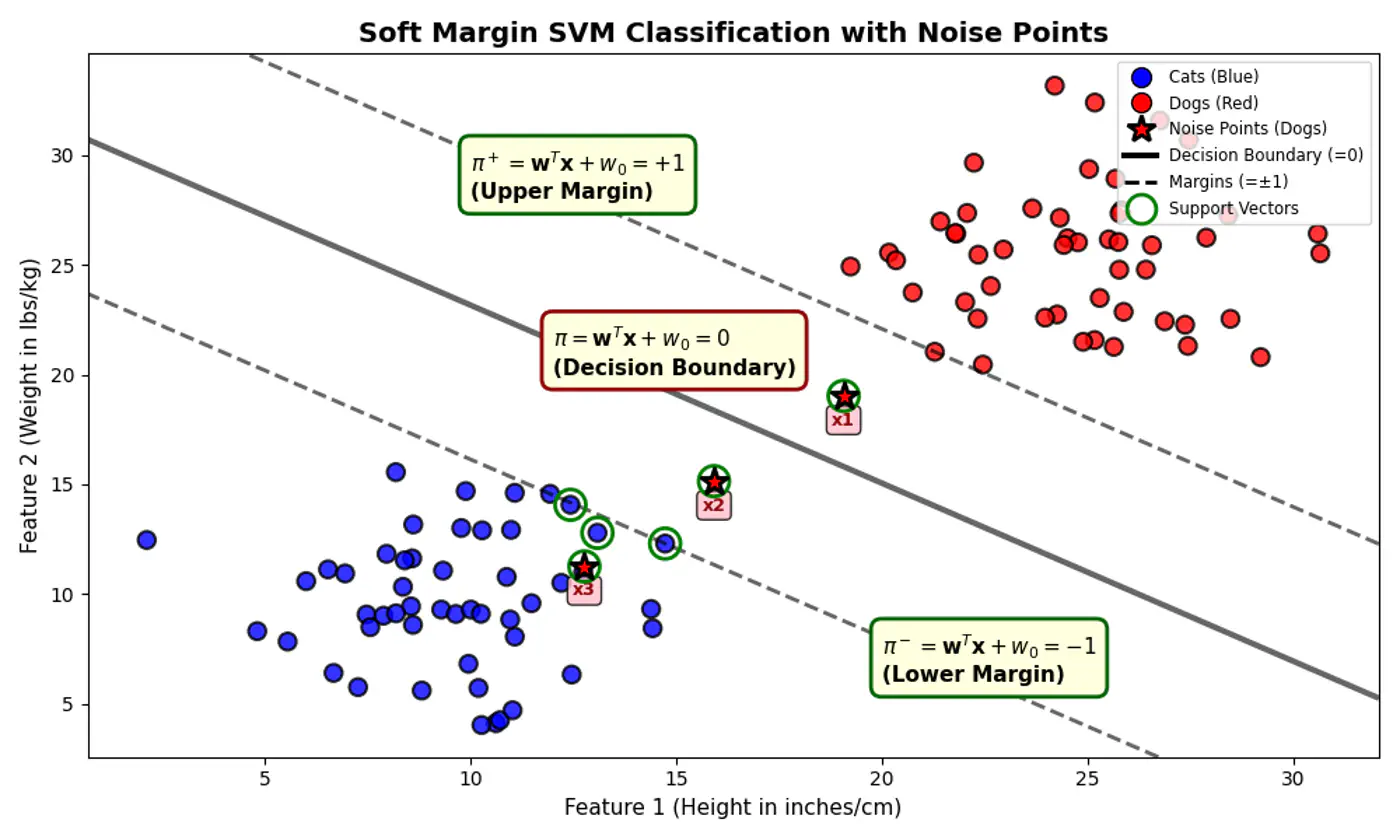
Distance from decision boundary:
- Distance of positive labelled points must be \(\ge 1\)
- But, distance of noise 📢 points (actually positive points) \(x_1, x_2 ~\&~ x_3\) < 1
⚔️ So, we introduce a slack variable or allowance for error term, \(\xi_i\) (pronounced ‘xi’) for every single data point.
\[y_i.(w^Tx_i + w_0) \ge 1 - \xi_i, ~ \forall i = 1,2,\dots, n\]\[ \implies \xi_i \ge 1 - y_i.(w^Tx_i + w_0) \\ also, ~ \xi_i \ge 0 \]\[So, ~ \xi _{i}=\max (0,1-y_{i}\cdot (w^Tx_i + w_0))\]Note: The above error term is also called ‘Hinge Loss’.
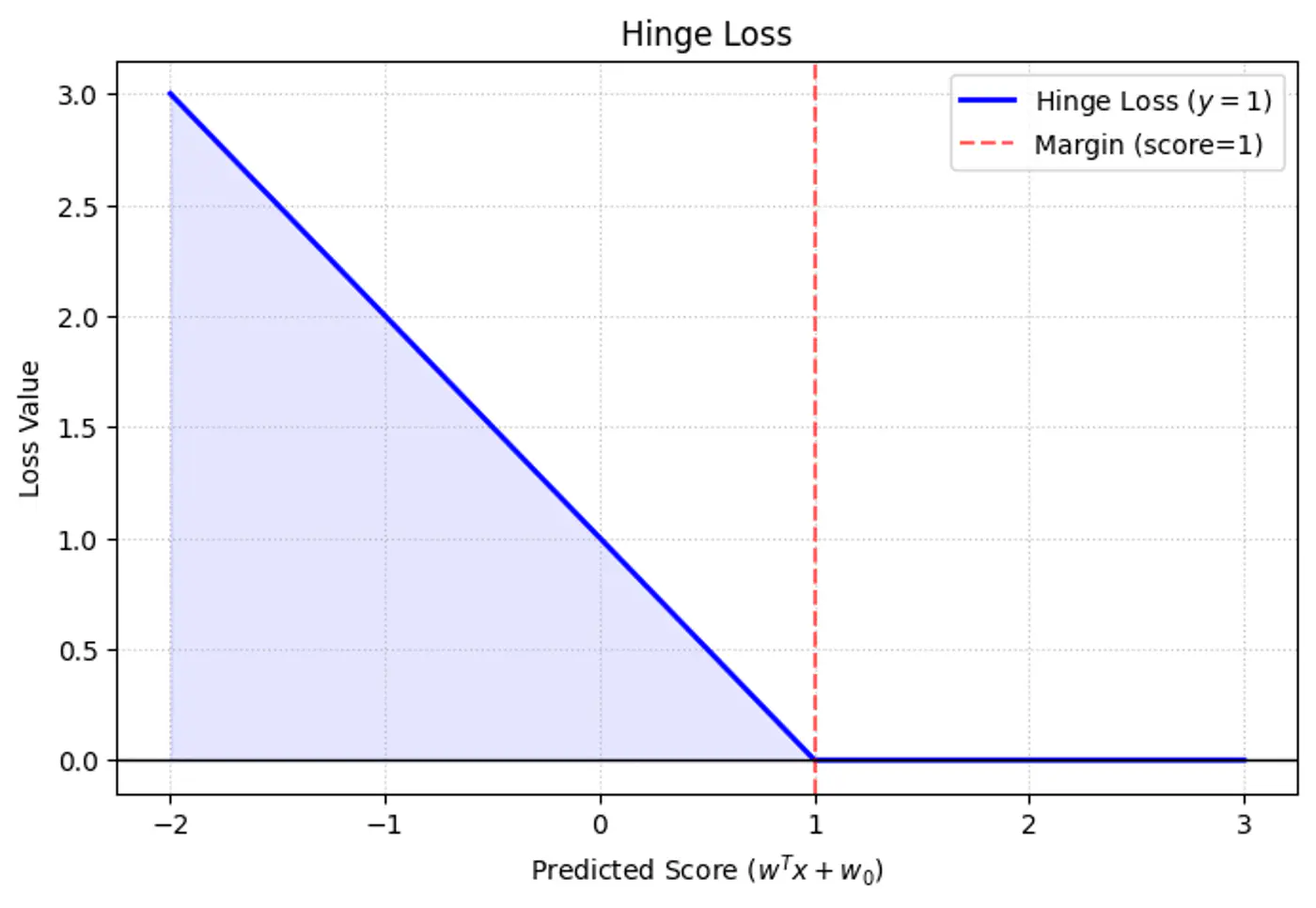
Hinge

- \(\xi_i = 0\) : Correctly classified and outside (or on) the margin.
- \(0 < \xi_i \le 1 \) : Within the margin but on the correct side of the decision boundary.
- \(\xi_i > 0\): On the wrong side of the decision boundary (misclassified).
e.g.: Since, the noise 📢 point are +ve (\(y_i=1\)) labeled:
\[\xi _{i}=\max (0,1-f(x_{i}))\]\(x_1, (d=+0.5)\): \(\xi _{i}=\max (0,1-0.5) = 0.5\)
\(x_2, (d=-0.5)\): \(\xi _{i}=\max (0,1-(-0.5))= 1.5\)
\(x_3, (d=-1.5)\): \(\xi _{i}=\max (0,1-(-1.5)) = 2.5\)
Subject to constraints:
- \(y_i(w^T x_i + b) \geq 1 - \xi_i\): The ‘softened’ margin constraint.
- \(\xi_i \geq 0\): Slack/Error cannot be negative.
Note: We use a hyper-parameter ‘C’ to control the trade-off.
- Large ‘C’: Over-Fitting;
Misclassifications are expensive 💰.
Model tries to keep the errors as low as possible. - Small ‘C’: Under-Fitting;
Margin width is more important than individual errors.
Model will ignore outliers/noise to get a ‘cleaner’(wider) boundary.
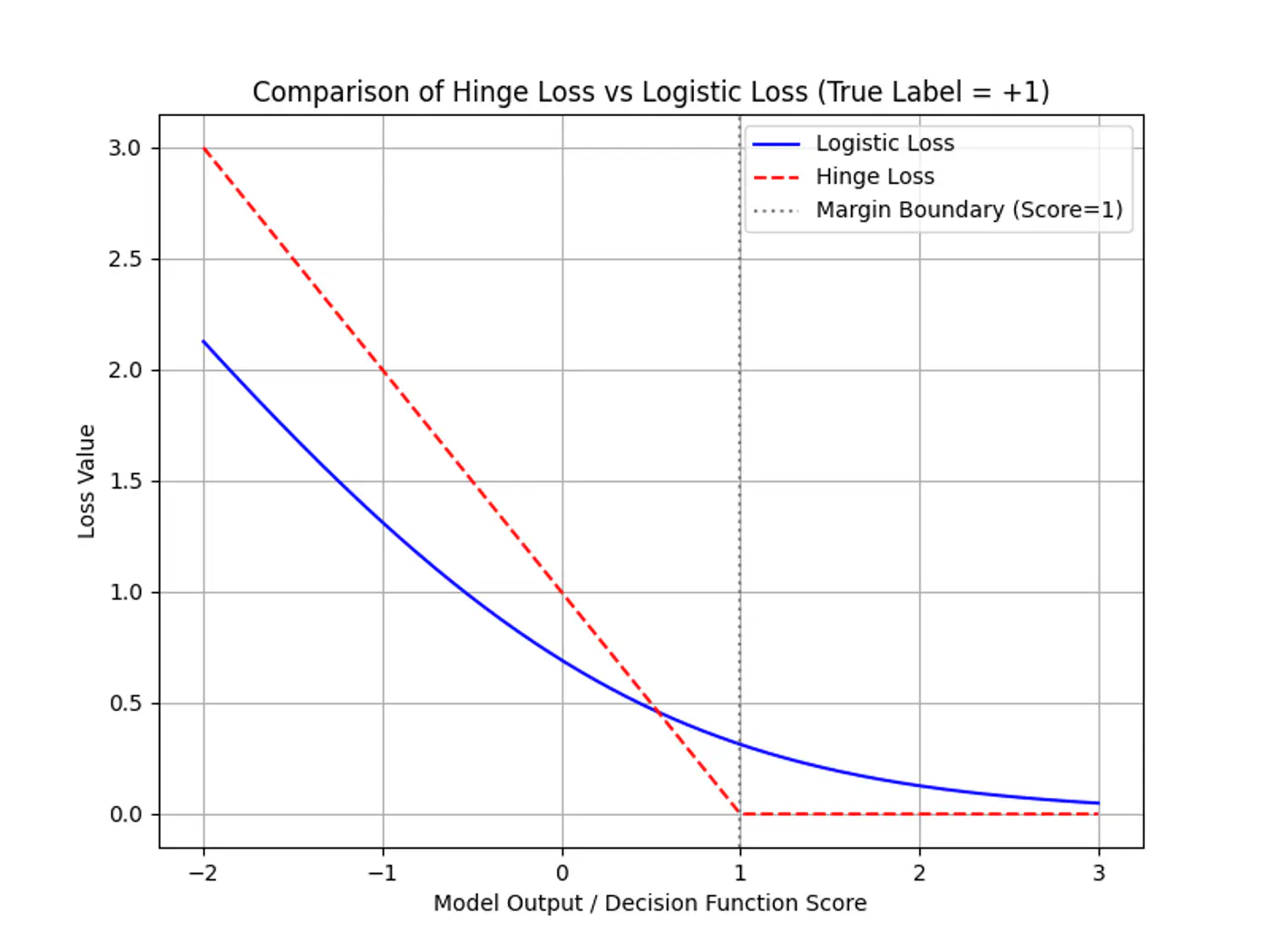
Note: SVM is just L2-Regularized Hinge Loss minimization, as Logistic Regression minimizes Log-Loss.
End of Section