Elliptic Envelope

Elliptic Envelope

  3 minute read  


Use Case 🐝

Detect anomalies in multivariate Gaussian data, such as, biometric data (height/weight) where features are normally distributed and correlated.

Assumption: The data can be modeled by a Gaussian distribution.

Intuition 💡

In a normal distribution, most data points cluster around the mean, and the probability density decreases as we move farther away from the center.

images/machine_learning/unsupervised/anomaly_detection/elliptic_envelope/slide_03_01.png
Issue with Euclidean Distance 🐲

🌍 Euclidean distance measures the simple straight-line distance from the center of the cloud.

👉If the data is spherical, this works fine.

🦕 However, real-world data is often stretched or skewed (e.g., taller people are generally heavier), due to correlations between variables, forming an elliptical shape.

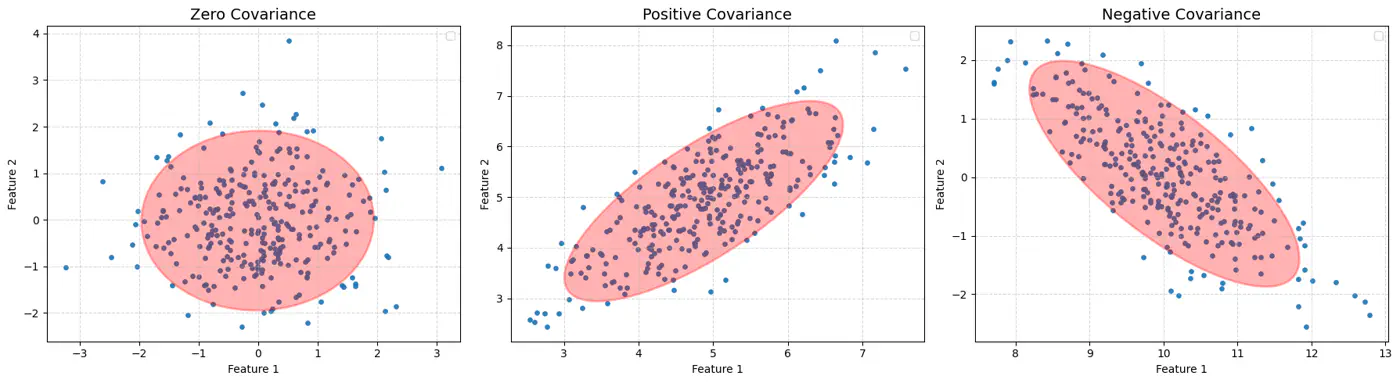
images/machine_learning/unsupervised/anomaly_detection/elliptic_envelope/slide_05_01.png
Mahalanobis Distance (Solution)

⭐️Mahalanobis distance essentially re-scales the data so that the elliptical distribution appears spherical, and then measures the Euclidean distance in that transformed space.

👉This way, it measures how many standard deviations(\(\sigma\)) away a point is from the mean, considering the data’s spread and correlation (covariance).

\[D_M(x) = \sqrt{(x - \mu)^T \Sigma^{-1} (x - \mu)}\]
Problem 🦀
Standard methods (like Z-score \(z = \frac{x-\mu}{\sigma}\)) fail because they are easily skewed by the outliers they are trying to find.
Solution 🦉
💡Instead of using all data, we find a ‘clean’ subset of the data that is most tightly packed and use only that subset to define the ‘normal’ ellipse.
Goal 🎯

👉Find the most dense core of the data.

\[D_M(x) = \sqrt{(x - \mu)^T \Sigma^{-1} (x - \mu)}\]

🦣 Determinant of covariance matrix \(\Sigma\) represents the volume of the ellipsoid.

⏲️ Therefore, minimize \(|\Sigma|\) to find the tight core.

👉 \(\text {Small} ~ \Sigma \rightarrow \text {Large} ~\Sigma ^{-1}\rightarrow \text {Large} ~ D_{M} ~\text {for outliers}\)

Minimum Covariance Determinant (MCD) Algorithm ⚙️

MCD algorithm is used to find the covariance matrix \(\Sigma\) with minimum determinant, so that the volume of the ellipsoid is minimized.

  1. Initialization: Select several random subsets of size h < n (default h = \(\frac{n+d+1}{2}\), d = # dimensions), representing ‘robust’ majority of the data.
  2. Calculate preliminary mean (\(\mu\)) and covariance (\(\Sigma\)) for each random subset.
  3. Concentration Step: Iterative core of the algorithm designed to ‘tighten’ the ellipsoid.
    • Calculate Distances: Compute the Mahalanobis distance of all ’n’ points in the dataset from the current subset’s mean (\(\mu\)) and covariance (\(\Sigma\)).
    • Select New Subset: Identify the ‘h’ points with the smallest Mahalanobis distances.
      • These are the points most centrally located relative to the current ellipsoid.
    • Update Estimates: Calculate a new and based only on these ‘h’ most central points.
    • Repeat 🔁: The steps repeat until the determinant stops shrinking.

Note: Select the best subset that achieved the absolute minimum determinant.

Limitations
  • Assumptions
    • Gaussian data.
    • Unimodal data (single center).
  • Cost 💰of covariance matrix \(\Sigma^{-1}\) inversion is O(d^3).

Elliptic Envelope | Anomaly Detection | Minimum Covariance Determinant (MCD)| Explained with Example


End of Section