Isolation Forest

Isolation Forest

  3 minute read  

PlaylistAnomaly Detection | All Videos
Use Case

‘Large scale tabular data.’

Credit card fraud detection in datasets with millions of rows and hundreds of features.

Note: Supervised learning requires balanced, labeled datasets (normal vs. anomaly), which are rarely available in real-world scenarios like fraud or cyber-attacks.

Intuition

‘Flip the logic.’

‘Anomalies’ are few and different, so they are much easier to isolate from the rest of the data than normal points.

Problem

‘Curse of dimensionality.’

Distance based (K-NN), and density based (LOF) algorithms require calculation of distance between all pair of points.

As the number of dimensions and data points grows, these calculations become exponentially more expensive and less effective.

Solution
Use a tree-based approach with better time complexity O(nlogn), making it highly scalable for massive datasets and robust in high-dimensional spaces without needing expensive distance metrics.
Goal

‘Randomly partition the data.’

If a point is an outlier, it will take fewer partitions (splits) to isolate it into a leaf node compared to a point that is buried deep within a dense cluster of normal data.

Isolation Forest (iForest)

Isolation Forest uses an ensemble of ‘Isolation Trees’ (iTrees) .

iTree (Isolation Tree) is a proper binary tree structure specifically designed to separate individual data points through random recursive partitioning.

Algorithm
  1. Sub-sampling:
    • Select a random subset of data (typically 256 instances) to build an iTree.
  2. Tree Construction: Randomly select a feature.
    • Randomly select a split value between the minimum and maximum values of that feature.
    • Divide the data into two branches based on this split.
    • Repeat recursively until the point is isolated or a height limit is reached.
  3. Forest Creation:
    • Repeat the process to create ‘N’ trees (typically 100).
  4. Inference:
    • Pass a new data point through all trees, calculate the average path length, and compute the anomaly score.
Scoring Function

Assign an anomaly score based on the path length h(x) required to isolate a point ‘x’.

  • Path Length (h(x)): The number of edges ‘x’ traverses from the root node to a leaf node.
  • Average Path Length (c(n)): Since iTrees are structurally similar to Binary Search Trees (BST), the average path length for a dataset of size ’n’ is given by: \[c(n)=2H(n-1)-\frac{2(n-1)}{n}\]

where, H(i) is the harmonic number, estimated as \(\ln (i)+0.5772156649\) (Euler’s constant).

Anomaly Score

To normalize the score between 0 and 1, we define it as:

\[s(x,n)=2^{-\frac{E(h(x))}{c(n)}}\]

E(H(x)): is the average path length of across a forest of trees .

  • \(s\rightarrow 1\): Point is an anomaly; Path length is very short.
  • \(s\approx 0.5\): Point is normal, path length approximately equal to c(n).
  • \(s\rightarrow 0\): Point is normal; deeply buried point, path length is much larger than c(n).
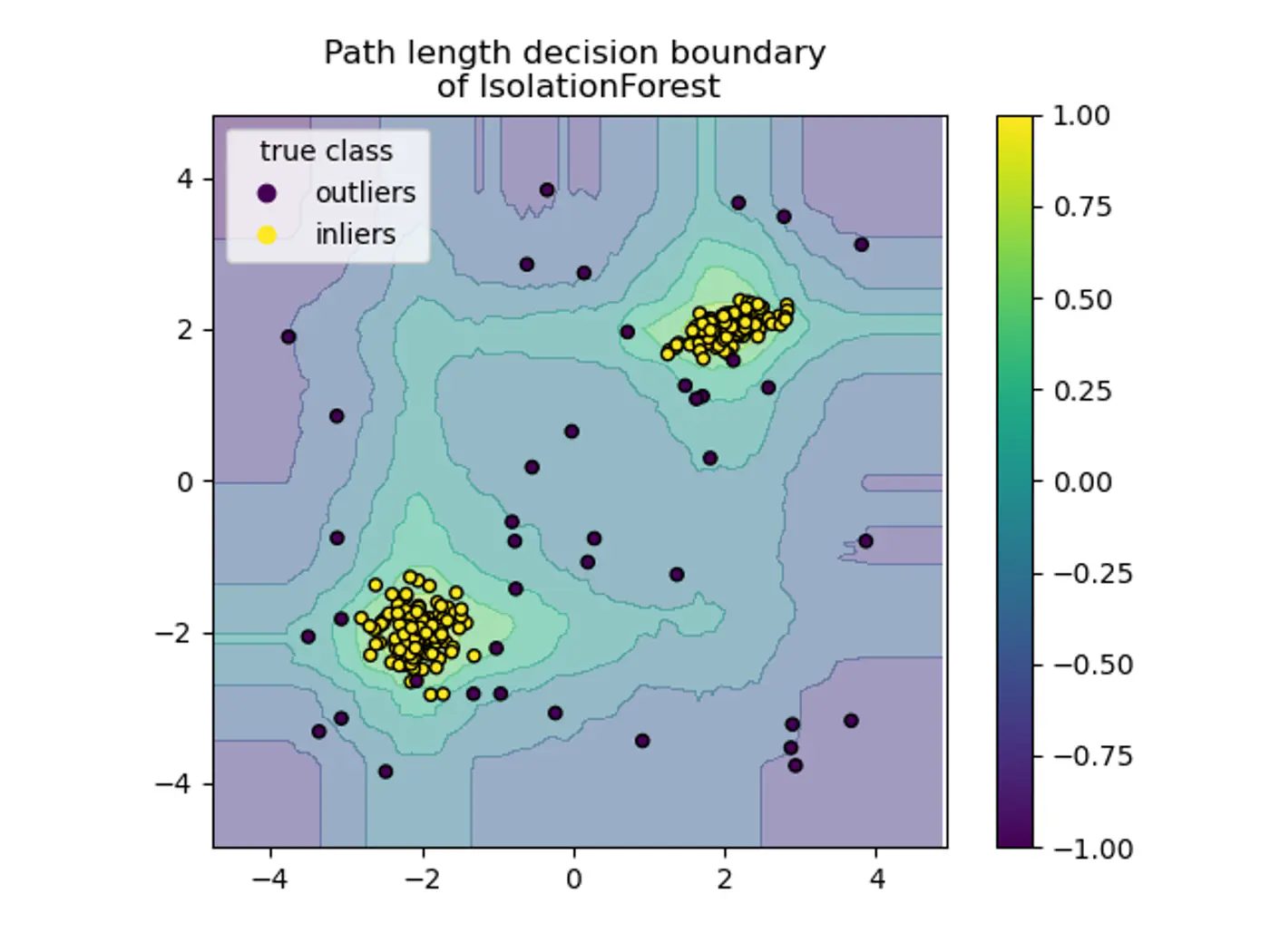
images/machine_learning/unsupervised/anomaly_detection/isolation_forest/slide_12_01.tif
Drawbacks
  • Axis-Parallel Splits:
    • Standard iTrees split only on one feature at a time, so:
      • We do not get a smooth decision boundary.
      • Anything off-axis has a higher probability of being marked as an outlier.
      • Note: Extended Isolation Forest fixes this by using random slopes.
  • Score Sensitivity: The threshold for what constitutes an ‘anomaly’ often requires manual tuning or domain knowledge.
Video Isolation Forest (iForest) | Anomaly Detection | Explained with Example

End of Section