Local Outlier Factor

Local Outlier Factor

  2 minute read  


Use Case 🐝
⭐️Geographic fraud detection:
A $100 transaction might be ‘normal’ in New York but an ‘outlier’ in a small rural village.
Intuition 💡

‘Local context matters.’

Global distance metrics fail when density is non-uniform.

🦄 An outlier is a point that is ‘unusual’ relative to its immediate neighbors, regardless of how far it is from the center of the entire dataset.

Problem 🦀

💡Traditional distance-based outlier detection methods, such as, KNN, often struggle with datasets where data is clustered at varying densities.

  • A point in a sparse region might be considered an outlier by a global method, even if it is a normal part of that sparse cluster.
  • Conversely, a point very close to a dense cluster might be an outlier relative to that specific neighborhood.
Solution 🦉

👉Calculate the relative density of a point compared to its immediate neighborhood.

e.g. If the neighbors are in a dense crowd and the point is not, it is an outlier.

Goal 🎯
📌Compare the density of a point to the density of its neighbors.
Local Outlier Factor (LOF)

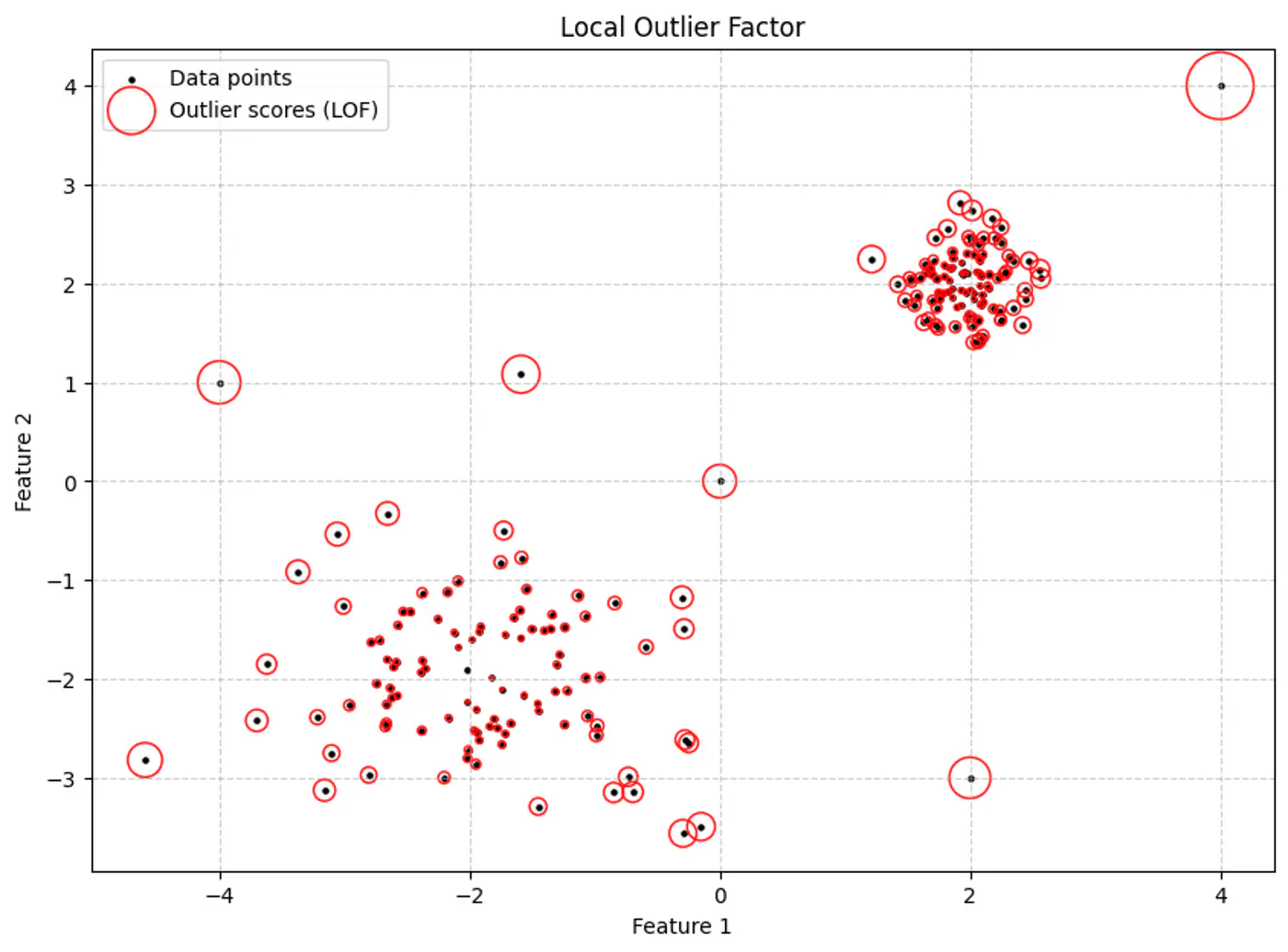
Local Outlier Factor (LOF) is a density-based algorithm designed to detect anomalies by measuring the local deviation of a data point relative to its neighbors.

👉Size of the red circle represents the LOF score.

images/machine_learning/unsupervised/anomaly_detection/local_outlier_factor/slide_08_01.png
LOF Score Calculation 🔢
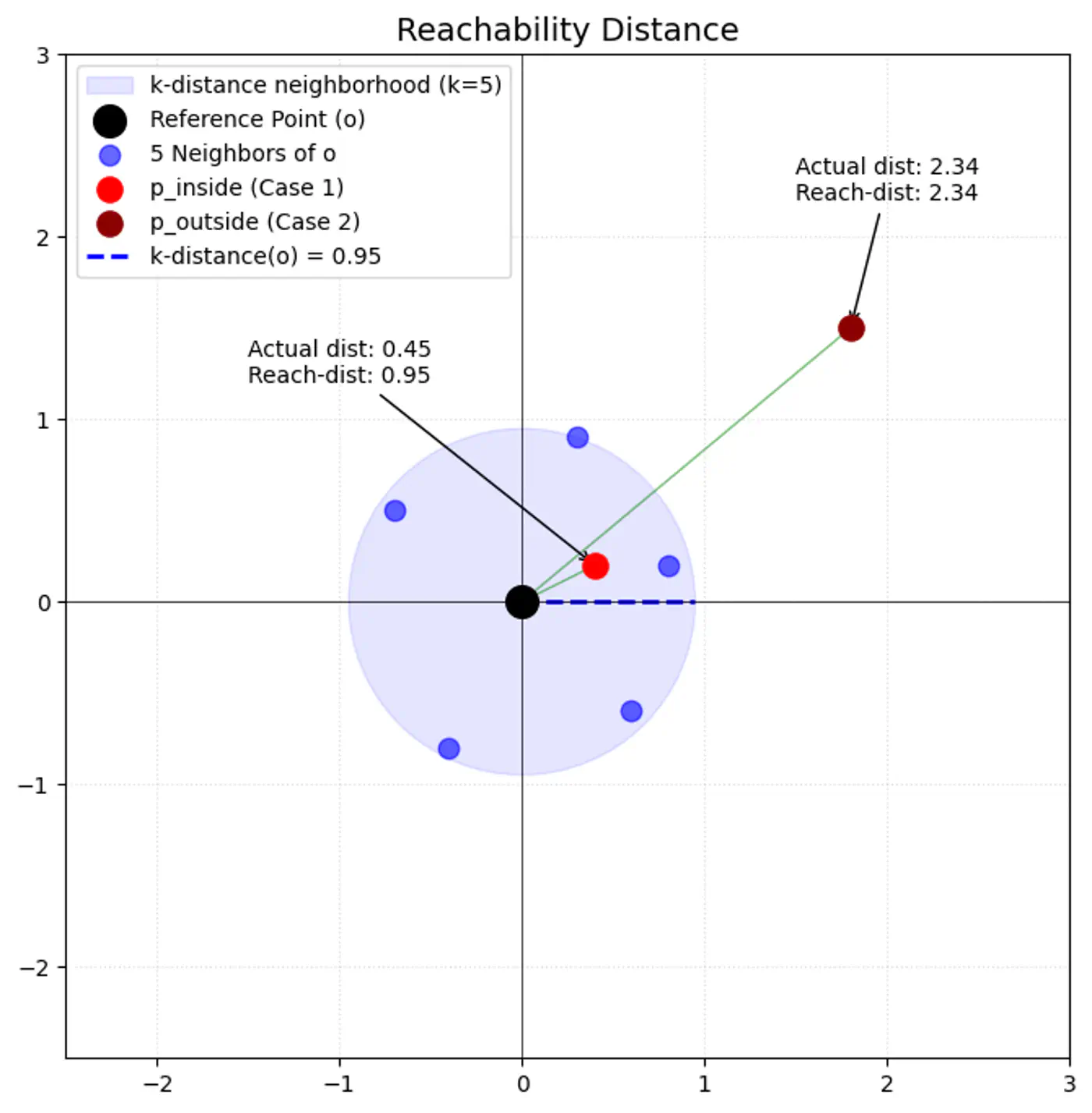
  1. K-Distance (\(k\text{-dist}(p)\)):
    • The distance from point ‘p’ to its k-th nearest neighbor.
  2. Reachability Distance (\(\text{reach-dist}_{k}(p,o)\)): \[\text{reach-dist}_{k}(p,o)=\max \{k\text{-dist}(o),\text{dist}(p,o)\}\]
    • \(\text{dist}(p,o)\): actual Euclidean distance between ‘p’ and ‘o’.
    • This acts as ‘smoothing’ factor.
    • If point ‘p’ is very close to ‘o’ (inside o’s k-neighborhood), round up distance to \(k\text{-dist}(o)\).
  3. Local Reachability Density (\(\text{lrd}_{k}(p)\)):
    • The inverse of the average reachability distance from ‘p’ to its k-neighbors (\(N_{k}(p)\)). \[\text{lrd}_{k}(p)=\left[\frac{1}{|N_{k}(p)|}\sum _{o\in N_{k}(p)}\text{reach-dist}_{k}(p,o)\right]^{-1}\]
      • High LRD: Neighbors are very close; the point is in a dense region.
      • Low LRD: Neighbors are far away; the point is in a sparse region.
  4. Local Outlier Factor (\(\text{LOF}_{k}(p)\)):
    • The ratio of the average ‘lrd’ of p’s neighbors to p’s own ‘lrd’. \[\text{LOF}_{k}(p)=\frac{1}{|N_{k}(p)|}\sum _{o\in N_{k}(p)}\frac{\text{lrd}_{k}(o)}{\text{lrd}_{k}(p)}\]
images/machine_learning/unsupervised/anomaly_detection/local_outlier_factor/slide_10_01.png
LOF Score 🔢 Interpretation
  • LOF ≈ 1: Point ‘p’ has similar density to its neighbors (inlier).
  • LOF > 1: Point p’s density is much lower than its neighbors’ density (outlier).

Local Outlier Factor (LOF) | Anomaly Detection | Explained with Example


End of Section