Gaussian Mixture Models

Introduction to Gaussian Mixture Models

  2 minute read  


Issue with K-Means
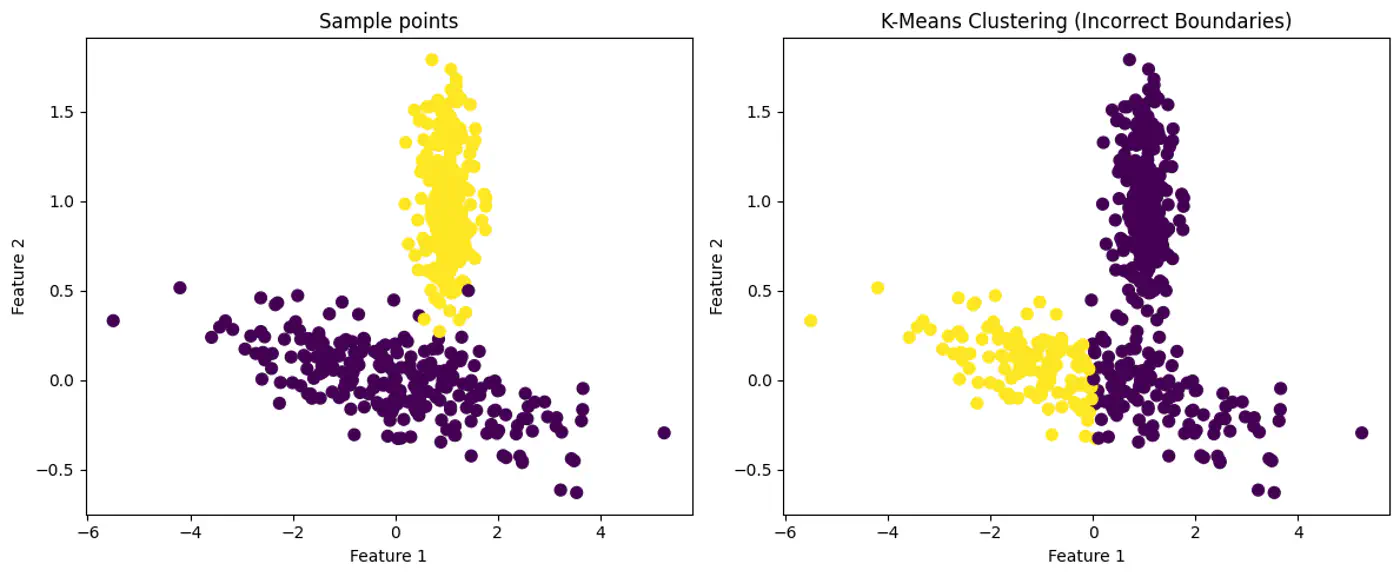
  • K-means uses Euclidean distance and assumes that clusters are spherical (isotropic) and have the same variance across all dimensions.
  • Places a circle or sphere around each centroid.
    • What if the clusters are elliptical ? 🤔

👉K-Means Fails with Elliptical Clusters.

images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/slide_02_01.png
Gaussian Mixture Model (GMM)

💡GMM: ‘Probabilistic evolution’ of K-Means

⭐️ GMM provides soft assignments and can model elliptical clusters by accounting for variance and correlation between features.

Note: GMM assumes that all data points are generated from a mixture of a finite number of Gaussian Distributions with unknown parameters.

👉GMM can Model Elliptical Clusters.

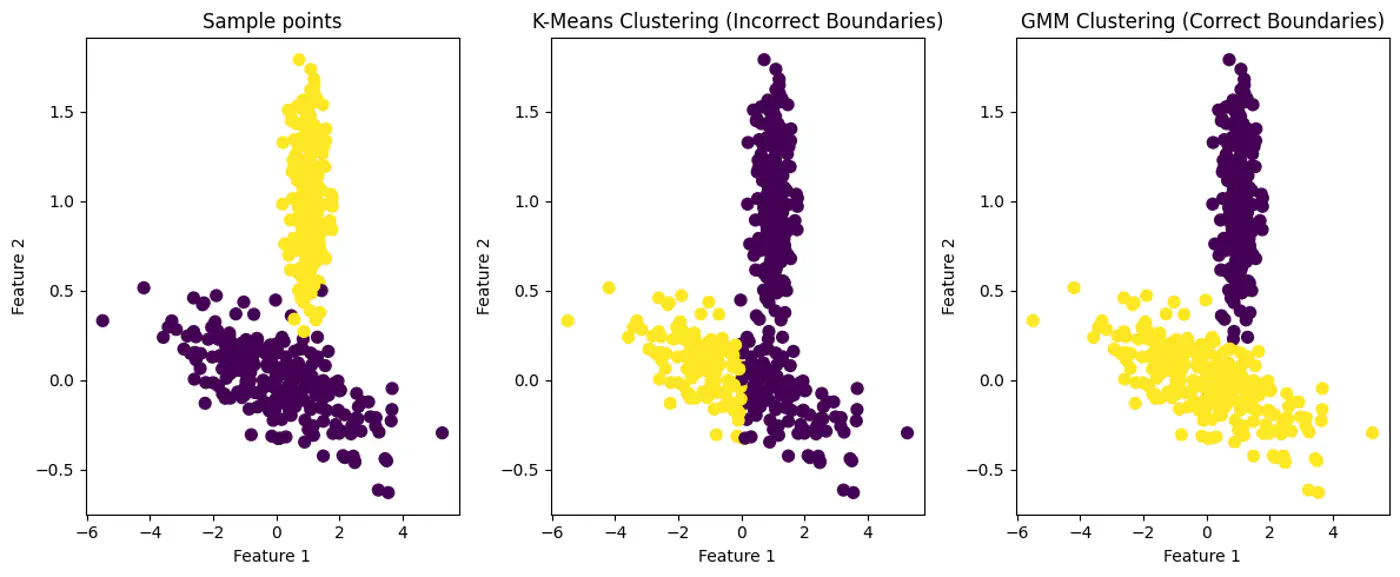
images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/slide_03_01.png
What is a Mixture Model

💡‘Combination of probability distributions’.

👉Soft Assignment: Instead of a simple ‘yes’ or ’no’ for cluster membership, a data point is assigned a set of probabilities, one for each cluster.

e.g: A data point might have a 60% probability of belonging to cluster ‘A’, 30% probability for cluster ‘B’, and 10% probability for cluster ‘C’.

👉Gaussian Mixture Model Example:

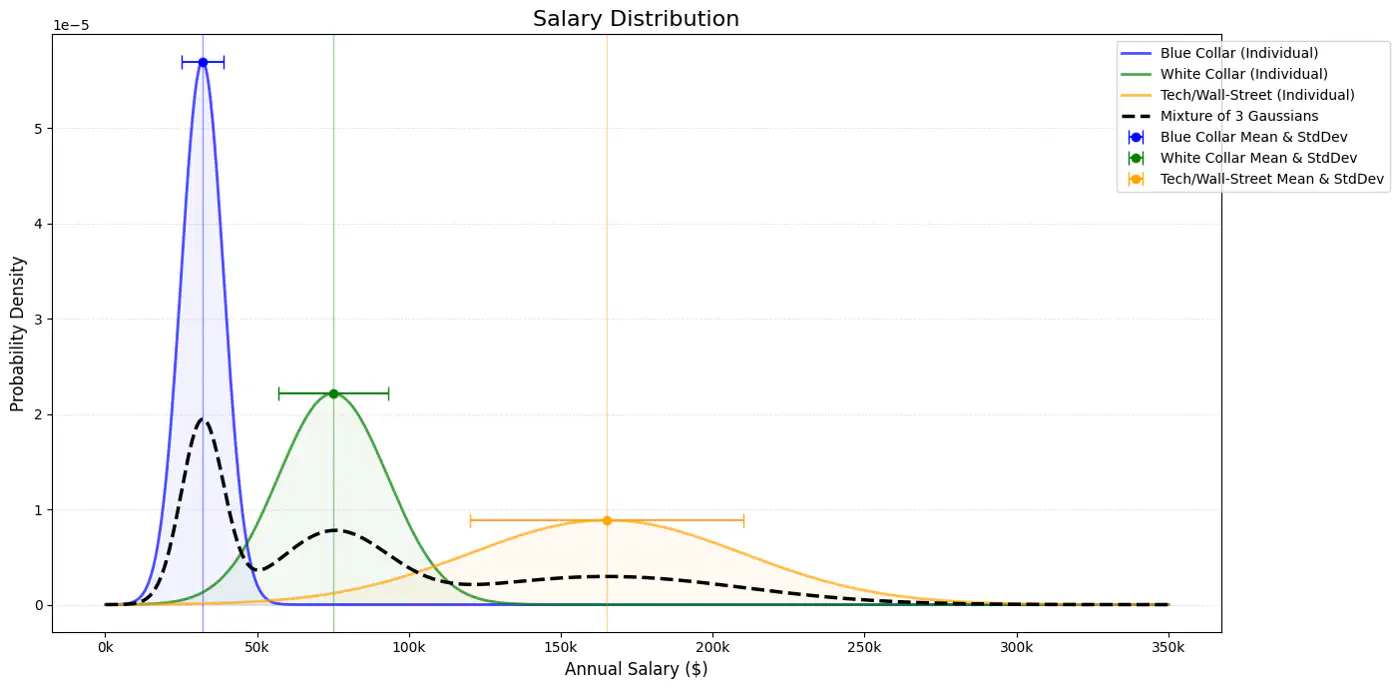
images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/slide_07_01.png
Gaussian PDF
\[{\displaystyle {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\sigma }})}: f(x\,|\,\mu ,\sigma ^{2})=\frac{1}{\sqrt{2\pi \sigma ^{2}}}\exp \left\{-\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right\}\]

\[ \text{ Multivariate Gaussian, } {\displaystyle {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})}: f(\mathbf{x}\,|\,\mathbf{\mu },\mathbf{\Sigma })=\frac{1}{\sqrt{(2\pi )^{n}|\mathbf{\Sigma }|}}\exp \left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu })^{T}\mathbf{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })\right\}\]

Note: The term \(1/(\sqrt{2\pi \sigma ^{2}})\) is a normalization constant to ensure the total area under the curve = 1.

👉Multivariate Gaussian Example:

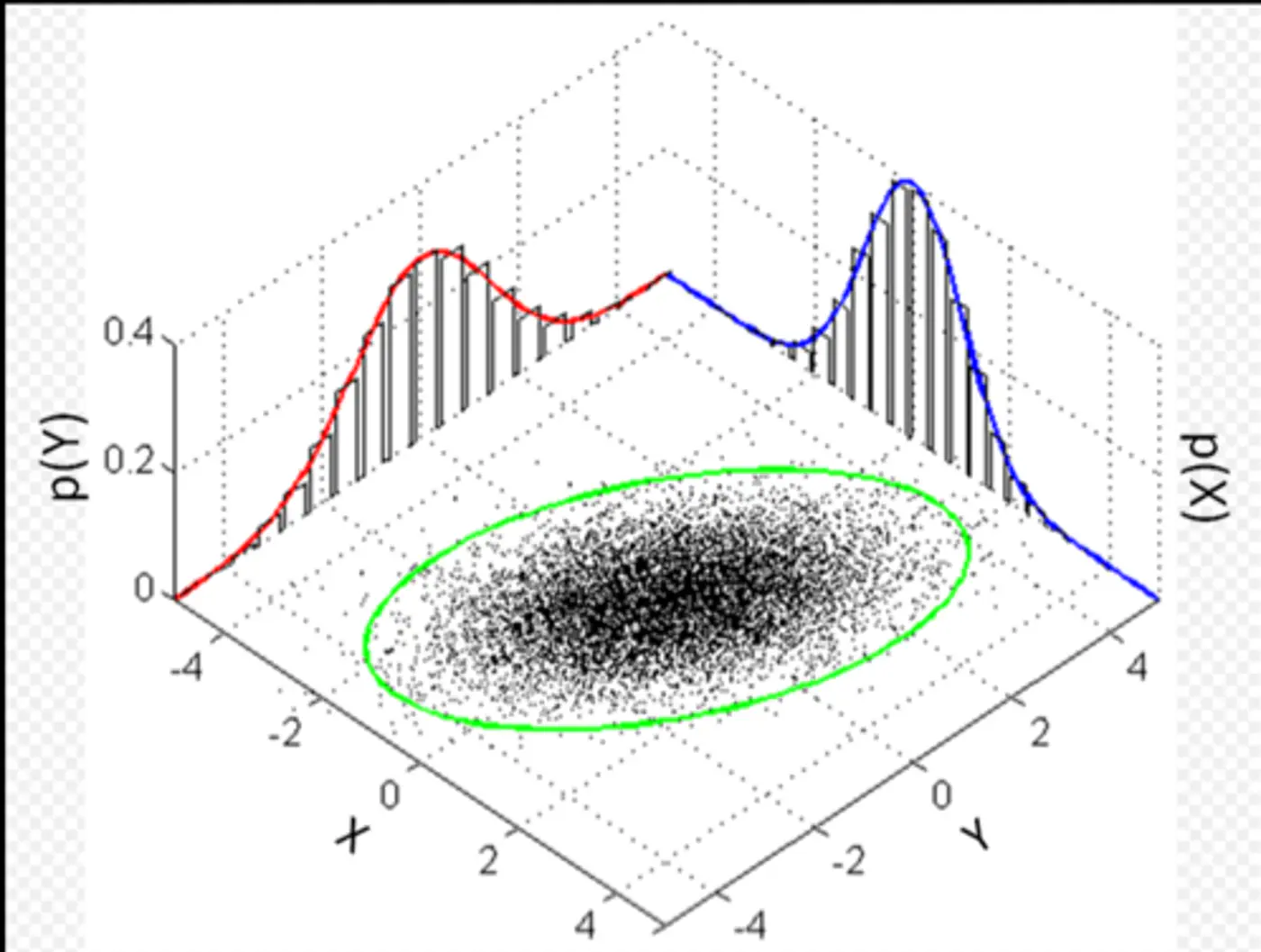
images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/slide_08_01.png
Gaussian Mixture

Whenever we have multivariate Gaussian, then the variables may be independent or correlated.

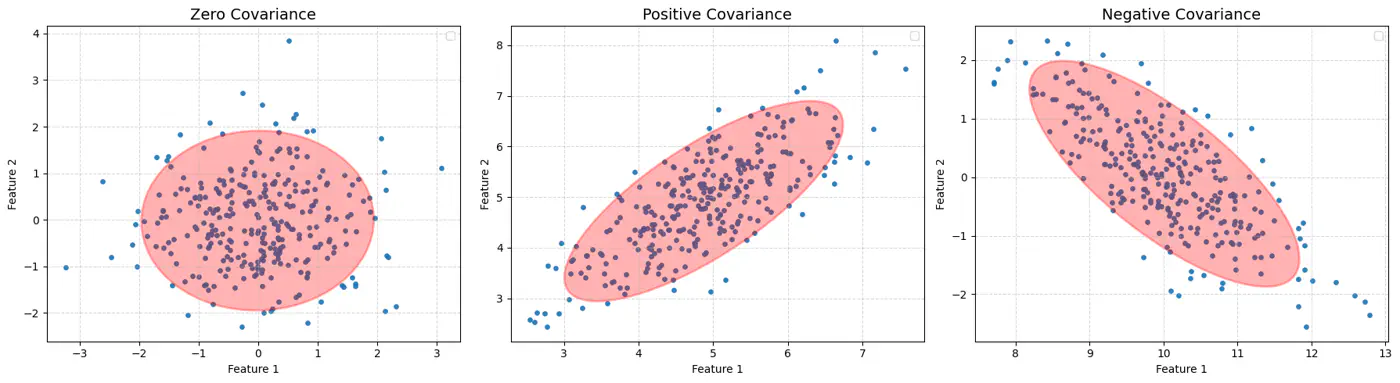
👉Feature Covariance:

images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/slide_10_01.png

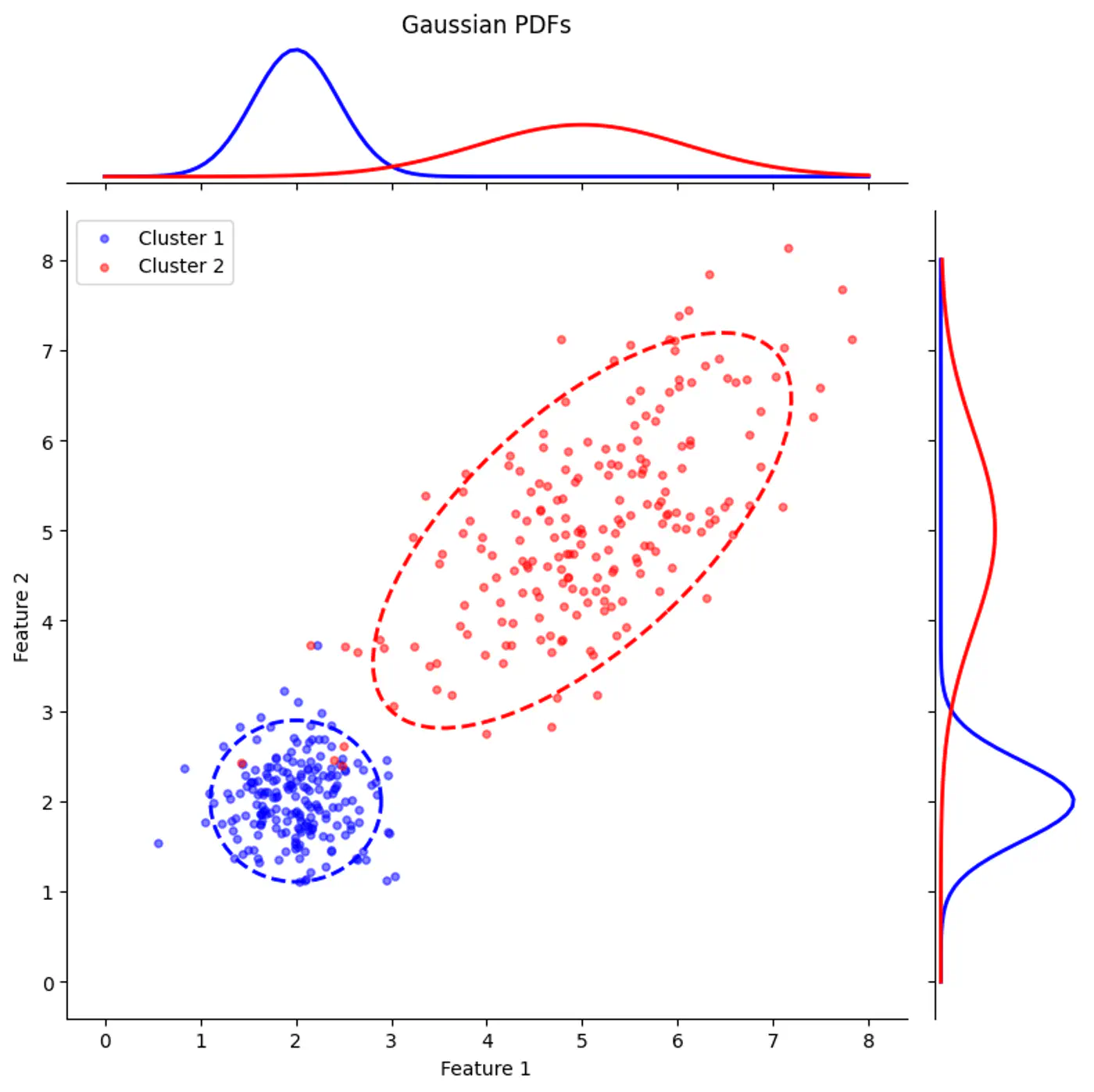
👉Gaussian Mixture with PDF

images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/slide_11_01.png

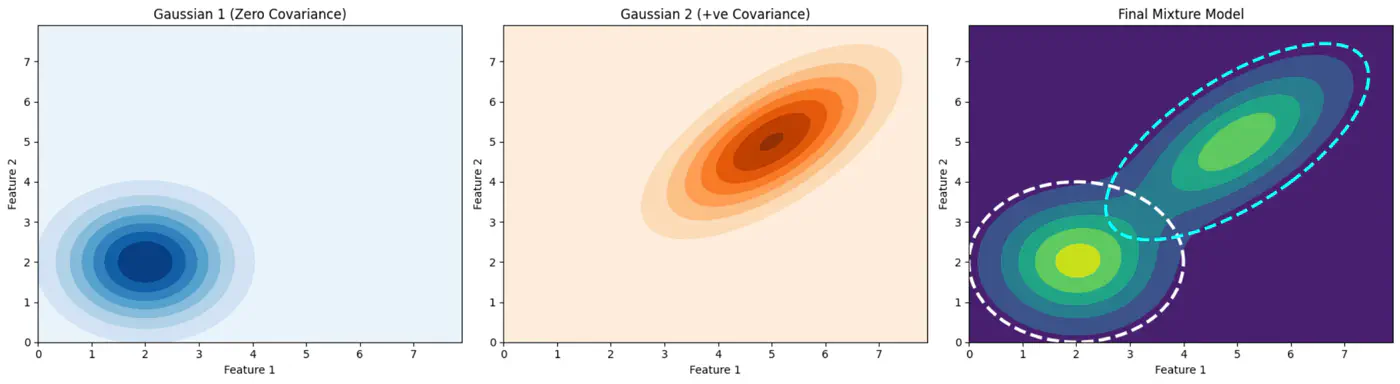
👉Gaussian Mixture (2D)

images/machine_learning/unsupervised/gaussian_mixture_model/introduction_gaussian_mixture_models/gmm_2d.png

Gaussian Mixture Model (GMM) | Foundational Concepts | Explained with Example


End of Section