K Means

🌍In real-world systems, labeled data is scarce and expensive 💰.

💡Unsupervised learning discovers inherent structure without human annotation.

👉Clustering answers: “Given a set of points, what natural groupings exist?”

• Customer Segmentation: Group users by behavior without predefined categories.
• Image Compression: Reduce color palette by clustering pixel colors.
• Anomaly Detection: Points far from any cluster are outliers.
• Data Exploration: Understand structure before building supervised models.
• Preprocessing: Create features from cluster assignments.

💡Clustering assumes that ‘similar’ points should be grouped together.

👉But what is ‘similar’? This assumption drives everything.

Given:

• Dataset X = {x₁, x₂, …, xₙ} where xᵢ ∈ ℝᵈ.
• Desired number of clusters ‘k'.

Find:

• Cluster assignments C = {C₁, C₂, …, Cₖ}.

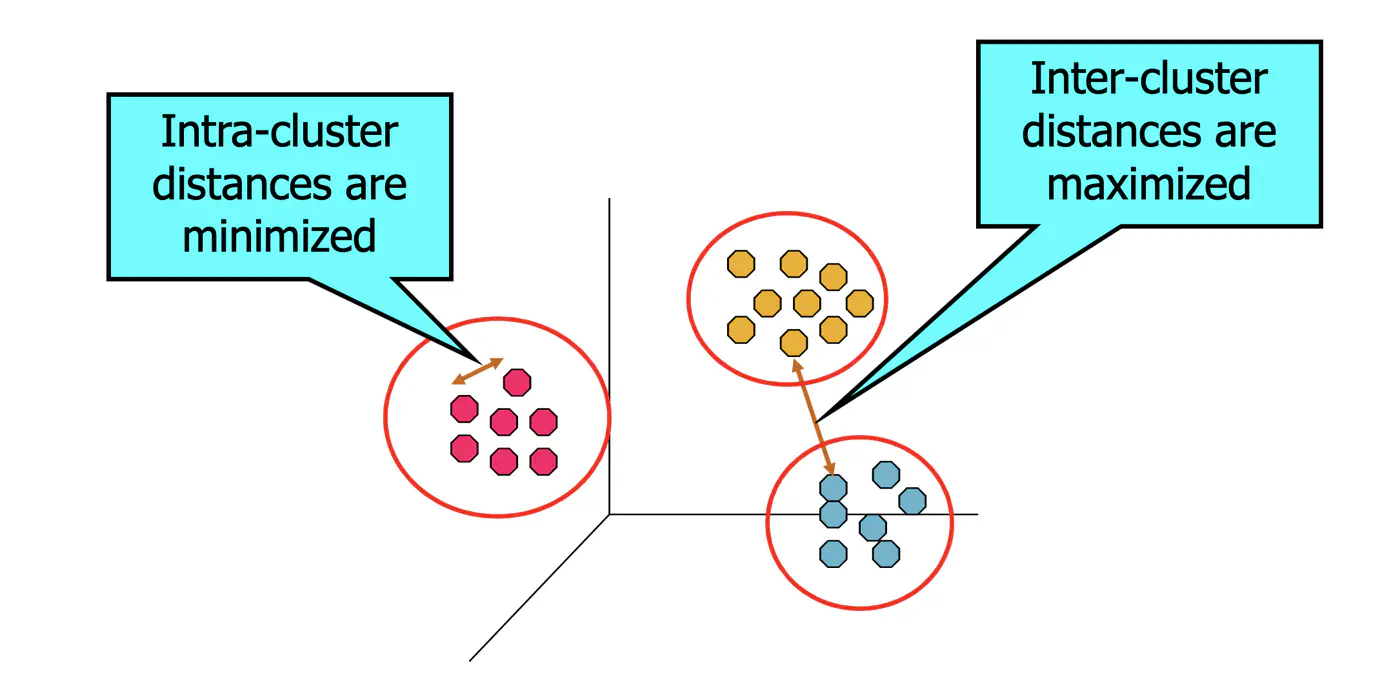
• Such that points within clusters are ‘similar’.

• And points across clusters are ‘dissimilar’.

  

This is fundamentally an optimization problem, i.e, find parameters such that the value is minimum/maximum. We need:

• An objective function
  • what makes a clustering ‘good’?
• An algorithm to optimize it
  • how do we find good clusters?
• Evaluation metrics
  • how do we measure quality?

Objective function:
👉Minimize the within-cluster sum of squares (WCSS).

• Where:
• C = {C₁, …, Cₖ} are cluster assignments.
• μⱼ is the centroid (mean) of cluster Cₖ.
• ||·||² is squared Euclidean distance.

Note: Every point belongs to one and only one cluster.

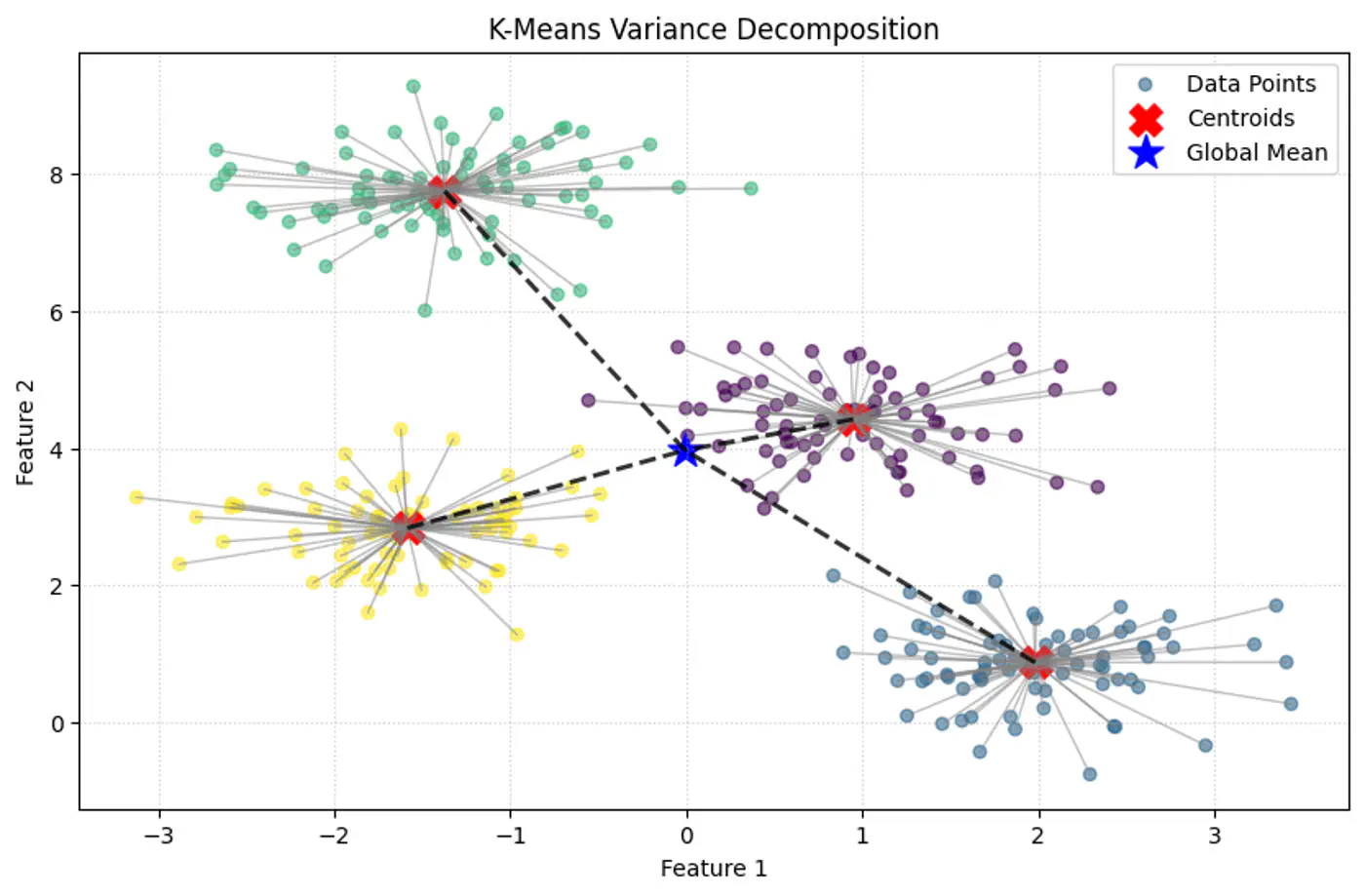
💡Within-Cluster Sum of Squares (WCSS) is nothing but variance.

⭐️ Total Variance = Within-Cluster Variance + Between-Cluster Variance

👉K-Means minimizes within-Cluster variance, which implicitly maximizes between-cluster separation.

Geometric Interpretation:

• Each point is ‘pulled’ toward its cluster center.
• The objective measures total squared distance of all points to their centers.
• Lower J(C, μ) means tighter, more compact clusters.

Note: K-Means works best when clusters are roughly spherical, similarly sized, and well-separated.

⭐️The problem requires partitioning ’n’ observations into ‘k’ distinct, non-overlapping clusters, which is given by the Stirling number of the second kind, which grows at a rate roughly equal to \(k^n/k!\).

👉This large number of possible combinations makes the problem NP-Hard.

🦉The k-means optimization problem is NP-hard because it belongs to a class of problems for which no efficient (polynomial-time ⏰) algorithm is known to exist.