K Means++

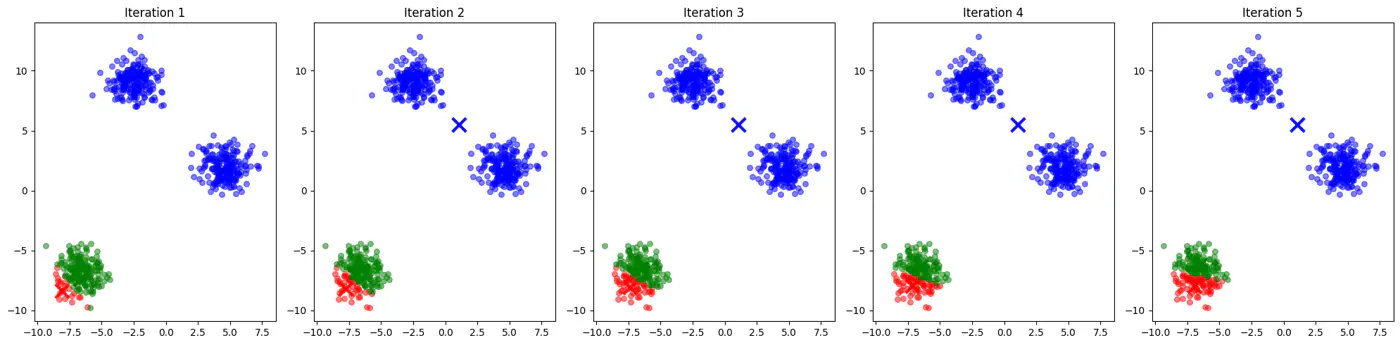
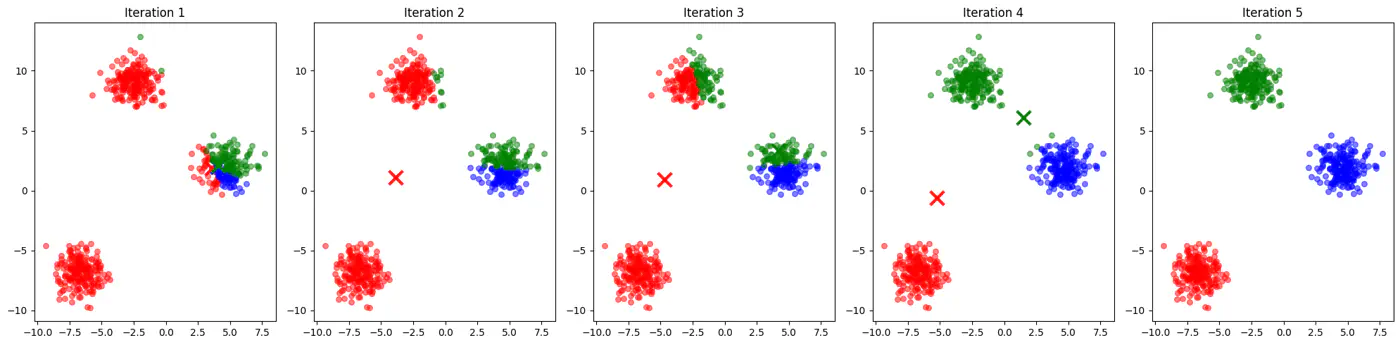
• If two initial centroids belong to the same natural cluster, the algorithm will likely split that natural cluster in half and be forced to merge two other distinct clusters elsewhere to compensate.
• Inconsistent; different runs may lead to different clusters.
• Slow convergence; Centroids may need to travel much farther across the feature space, requiring more iterations.

👉Example for different K-Means algorithm runs give different clusters

💡Addresses the issue due to random initialization by aiming to spread out the initial centroids across the data points.

Steps:

1. Select the first centroid: Choose one data point randomly from the dataset to be the first centroid.
2. Calculate distances: For every data point x not yet selected as a centroid, calculate the distance, D(x), between x and the nearest centroid chosen so far.
3. Select the next centroid: Choose the next centroid from the remaining data points with a probability proportional to D(x)^2.
   This makes it more likely that a point far from existing centroids is selected, ensuring the initial centroids are well-dispersed.
4. Repeat: Repeat steps 2 and 3 until ‘k’ number of centroids are selected.
5. Run standard K-means: Once the initial centroids are chosen, the standard k-means algorithm proceeds with assigning data points to the nearest centroid and iteratively updating the centroids until convergence.