Lloyds Algorithm
Lloyds Algorithm
2 minute read
Idea 💡
Since, we cannot enumerate all partitions (i.e, partitioning ’n’ observations into ‘k’ distinct, non-overlapping clusters),
Lloyd’s algorithm provides a local search heuristic (approximate algorithm).
Lloyd's Algorithm ⚙️
Iterative method for partitioning ’n’ data points into ‘k’ groups by repeatedly assigning data points to the nearest centroid (mean) and then recalculating centroids until assignments stabilize, aiming to minimize within-cluster variance.
📥Input: X = {x₁, …, xₙ}, ‘k’ (number of clusters)
📤Output: ‘C’ (clusters), ‘μ’ (centroids)
👉Steps:
- Initialize: Randomly choose ‘k’ cluster centroids μ₁, …, μₖ.
- Repeat until convergence, i.e, until cluster assignments and centroids no longer change significantly.
- a) Assignment: Assign each data point to the cluster whose centroid is closest (usually using Euclidean distance).
- For each point xᵢ: cᵢ = argminⱼ ||xᵢ - μⱼ||²
- b) Update: Recalculate the centroid (mean) of each cluster.
- For each cluster j: μⱼ = (1/|Cⱼ|) Σₓᵢ∈Cⱼ xᵢ
Issues🚨
- Initialization sensitive, different initialization may lead to different clusters.
- Tries to make each cluster of same size that may not be the case in real world.
- Tries to make each cluster with same density(variance)
- Does not work well with non-globular(spherical) data.
👉See how 2 different runs of K-Means algorithm gives totally different clusters.
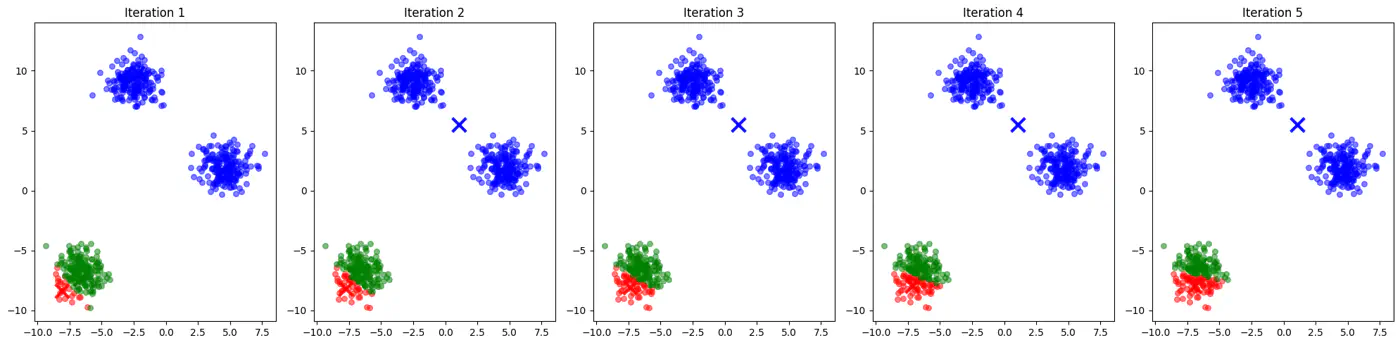
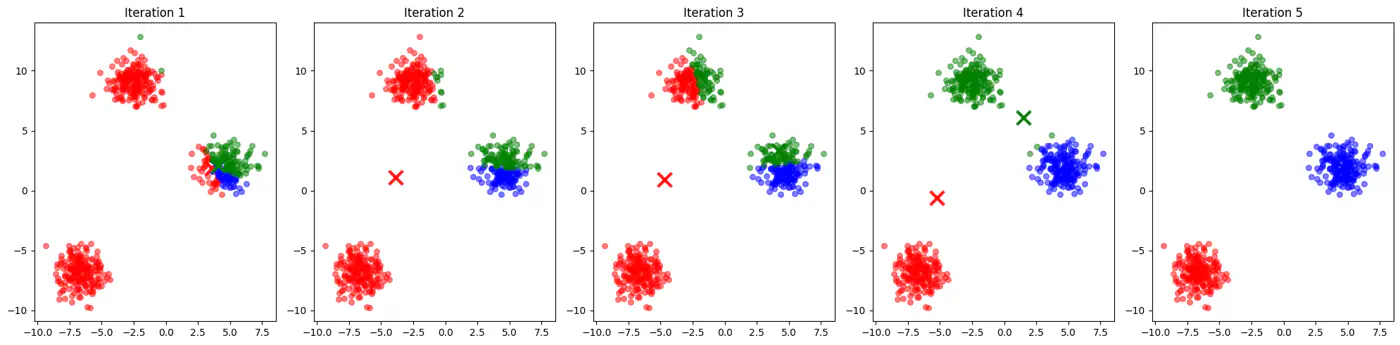
👉Also, K-Means does not work well with non-spherical clusters, or clusters with different densities and sizes.
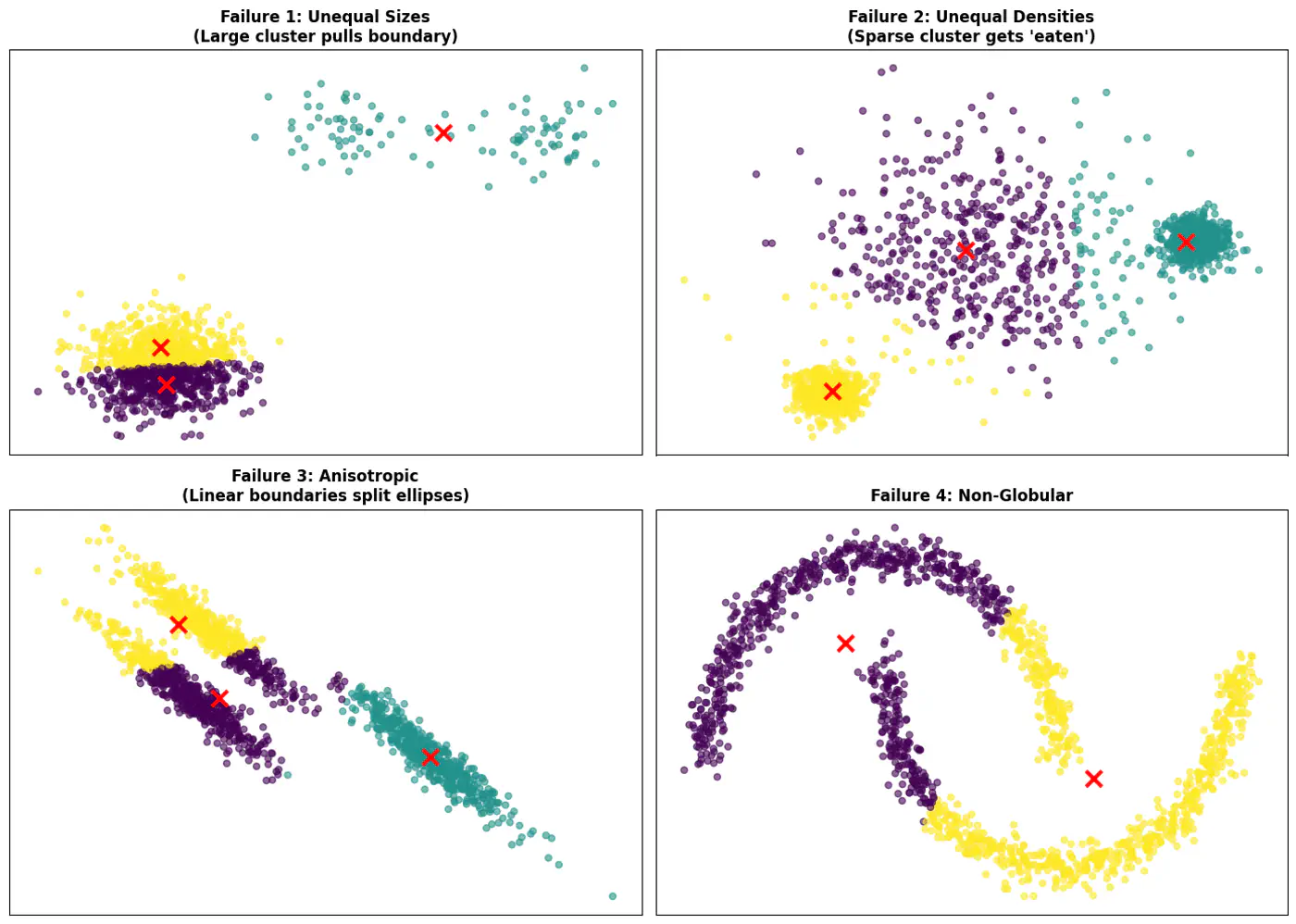
Solutions
✅ Do multiple runs 🏃♂️and choose the clustering with minimum error.
✅ Do not select initial points randomly, but some logic, such as, K-means++ algorithm.
✅ Use hierarchical clustering or density based clustering DBSCAN.
✅ Do not select initial points randomly, but some logic, such as, K-means++ algorithm.
✅ Use hierarchical clustering or density based clustering DBSCAN.
End of Section