Newton's Method

Newton’s Method for Optimization

  2 minute read  


Newton’s Method:
It is a second-order iterative gradient based optimization technique known for its extremely fast convergence.
When close to optimum, it achieves quadratic convergence, better than gradient descent’s linear convergence.

Algorithm:

  1. Start at a random point \(x_k\).
  2. Compute the slope at \(x_k, ~i.e,~ f'(x_k)\).
  3. Compute the curvature at \(x_k, ~i.e,~ f''(x_k)\).
  4. Draw a parabola at \(x_k\) that locally approximates the function.
  5. Jump directly to the minimum of that parabola; that’s the next step. Note: So, instead of walking down the slope step by step (gradient descent), we are jumping straight to the point where the curve bends downwards towards the bottom.
\[ x_{k+1} = x_k - \frac{f\prime(x_k)}{f\prime\prime(x_k)} \\[10pt] \text{ step size = } \frac{1}{f\prime\prime(x_k)} \\[10pt] f\prime\prime(x_k) : \text{ tells curvature of the function at } x_k \\[10pt] x_{new} = x_{old} - (\nabla^2 f(x_{old})^{-1} \nabla f(x_{old}) \\[10pt] \nabla^2 f(x_{old}): Hessian \]
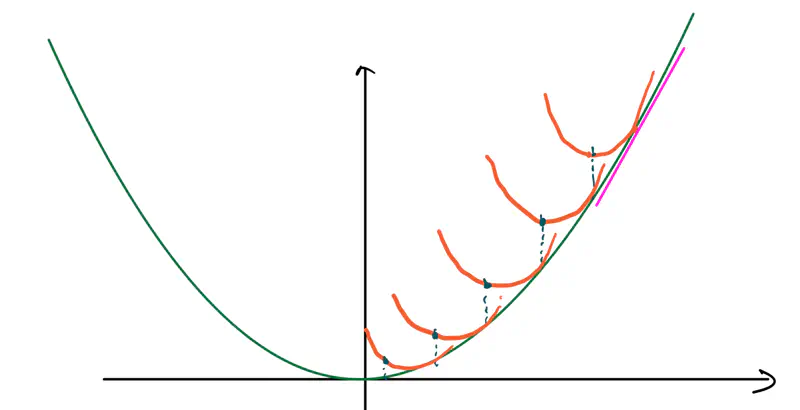
images/maths/calculus/optimization/newton_method.png
Example
  1. Find the minima of \(f(x) = x^2 - 4x + 5\) To find the minima, lets calulate the first derivative and equate to zero.
    \(f'(x) = 2x - 4 = 0 \)
    \( => x^* = 2 \)

    \(f''(x) = 2 >0 \) => minima is at \(x^* = 2\)

Now, we will solve this using Newton’s Method.
Let’s start at x = 0.

\[ x_{new} = x_{old} - \frac{f\prime(x_{old})}{f\prime\prime(x_{old}} \\[10pt] => x_{new} = 0 - \frac{2*0 -4}{2} = 0-(-2) \\[10pt] => x_{new} = 2 \]

Hence, we can see that using Newton’s Method we can get to the minima \(x^* = 2\) in just 1 step.

Limitations

Full Newton’s Method is rarely used in Machine Learning/Deep Learning optimization, because of the following limitations:

  1. \(TC = O(n^2\)) for Hessian calculation, since for a network with \(n\) parameters
    requires \(n^2\) derivative calculations.
  2. \(TC = O(n^3\)) for Hessian Inverse calculation.
  3. If it encounters a Saddle point, then it can go to a maxima rather than minima.

Because of the above limitations, we use Quasi-Newton methods like BFGS and L-BFGS.
The quasi-Newton methods make use of approximations for Hessian calculation, in order to gain the benefits of curvature without incurring the cost of Hessian calculation.

BFGS: Broyden-Fletcher-Goldfarb-Shanno
L-BFGS: Limited-memory BFGS

Newton's Method of Optimization | Machine Learning | Explained with Example


End of Section