Hyperplane

Equation of a Hyperplane

  5 minute read  


What is the equation of a line ?

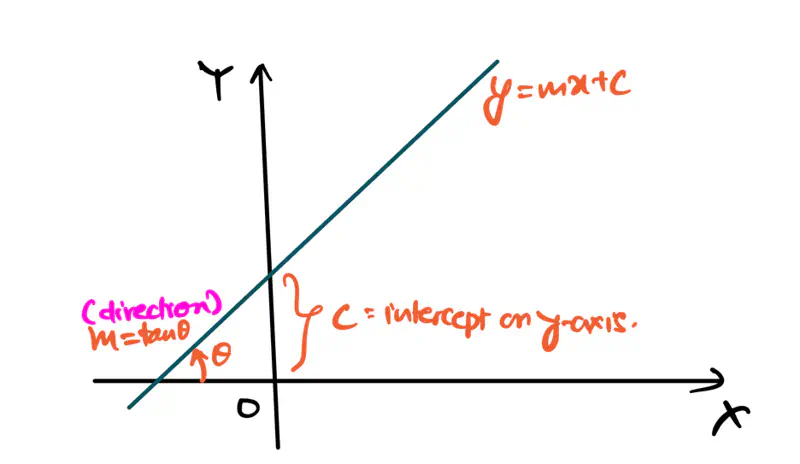
Equation of a line is of the form \(y = mx + c\).
To represent a line in 2D space, we need 2 things:

  1. m = slope or direction of the line
  2. c = y-intercept or distance from the origin
images/maths/linear_algebra/line.png
Hyperplane
A hyperplane is a lower (d-1) dimensional sub-space that divides a d-dimensional space into 2 distinct parts.
Equation of a Hyperplane

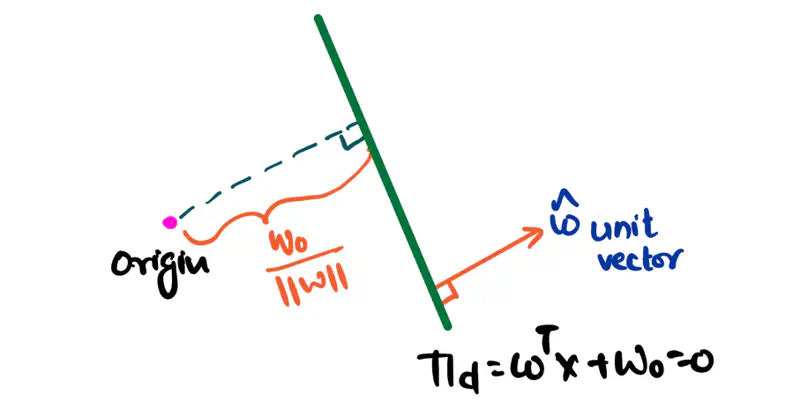
Similarly, to represent a hyperplane in d-dimensions, we need 2 things:

  1. \(\vec{w}\) = direction of the hyperplane = vector perpendicular to the hyperplane
  2. \(w_0\) = distance from the origin
\[ \pi_d = w_1x_1 + w_2x_2 + \dots + w_dx_d + w_0 = 0\\[10pt] \text{ representing 'w' and 'x' as vectors: } \\[10pt] \mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_d \end{bmatrix}_{\text{d×1}}, \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}_{\text{d×1}} \\[10pt] \pi_d = \mathbf{w}^\top \mathbf{x} + w_0 = 0 \\[10pt] => \mathbf{w} \cdot \mathbf{x} + w_0 = 0 \\[10pt] \text{ dividing both sides by the Euclidean norm of w: } \Vert \mathbf{w} \Vert_2 \\[10pt] \frac{\mathbf{w} \cdot \mathbf{x}}{\Vert \mathbf{w} \Vert} + \frac{w_0}{\Vert \mathbf{w} \Vert} = 0 \\[10pt] \text { since the vector divided by its magnitude is a unit vector, so: } \frac{\mathbf{w}}{\Vert \mathbf{w} \Vert} = \mathbf{\widehat{w}} \\[10pt] \mathbf{\widehat{w}} = \frac{w_1x_1 + w_2x_2 + \dots + w_dx_d}{\sqrt{w_1^2 + w_2^2 + \dots + w_d^2}} \\[10pt] \mathbf{\widehat{w}} \cdot \mathbf{x} + \frac{w_0}{\Vert \mathbf{w} \Vert} = 0 \\[10pt] \mathbf{\widehat{w}} \text{ : is the direction of the hyperplane } \\[10pt] \frac{w_0}{\Vert \mathbf{w} \Vert} \text{ : is the distance from the origin } \]

Note: There can be only 2 directions of the hyperplane, i.e, direction of a unit vector perpendicular to the hyperplane:

  1. Towards the origin
  2. Away from the origin
images/maths/linear_algebra/hyperplane.png
Distance from Origin

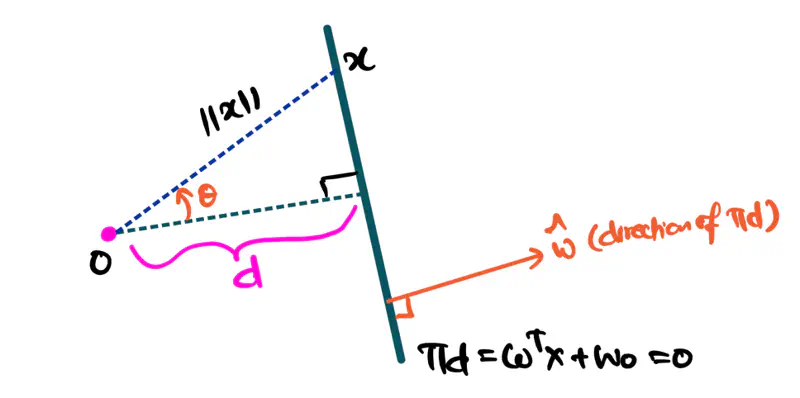
If a point ‘x’ is on the hyperplane, then it satisfies the below equation:

\[ \pi_d = \mathbf{w}^\top \mathbf{x} + w_0 = 0 \\ => {\Vert \mathbf{w} \Vert}{\Vert \mathbf{x} \Vert} cos{\theta} + w_0 = 0 \\[10pt] \because d = \text{ distance from the origin } = {\Vert \mathbf{x} \Vert} cos{\theta} \\ => {\Vert \mathbf{w} \Vert}.d = -w_0 \\[10pt] => d = \frac{-w_0}{{\Vert \mathbf{w} \Vert}} \\[10pt] \therefore distance(0, \pi_d) = \frac{-w_0}{\Vert \mathbf{w} \Vert} \]
images/maths/linear_algebra/hyperplane_distance.png

Key Points:

  1. By convention, the direction of the hyperplane is given by a unit vector perpendicular to the hyperplane , i.e, \({\Vert \mathbf{w} \Vert} = 1\), since the direction is only important.
  2. \(w_0\) gives the signed perpendicular distance from the origin.
    \(w_0 = 0\) => Hyperplane passes through the origin.
    \(w_0 < 0\) => Hyperplane is in the same direction of unit vector \(\mathbf{\widehat{w}}\) w.r.t the origin.
    \(w_0 > 0\) => Hyperplane is in the opposite direction of unit vector \(\mathbf{\widehat{w}}\) w.r.t the origin.
Consider a line as a hyperplane in 2D space. Let the unit vector point towards the positive x-axis direction.
What is the direction of the hyperplane w.r.t the origin and the direction of the unit vector ?

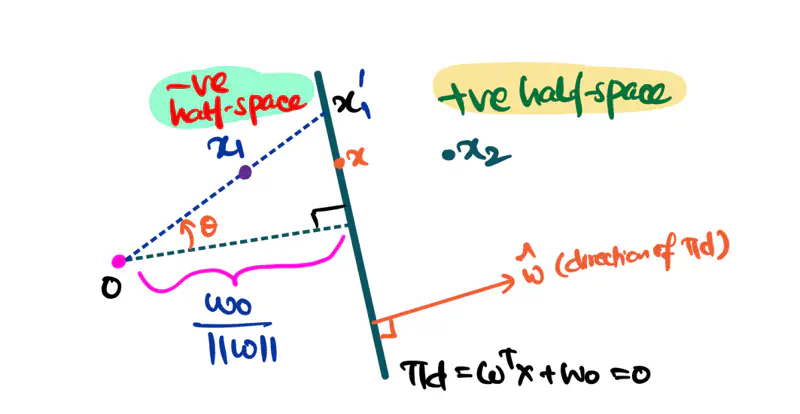
Equation of a hyperplane is: \(\pi_d = \mathbf{w}^\top \mathbf{x} + w_0 = 0\)
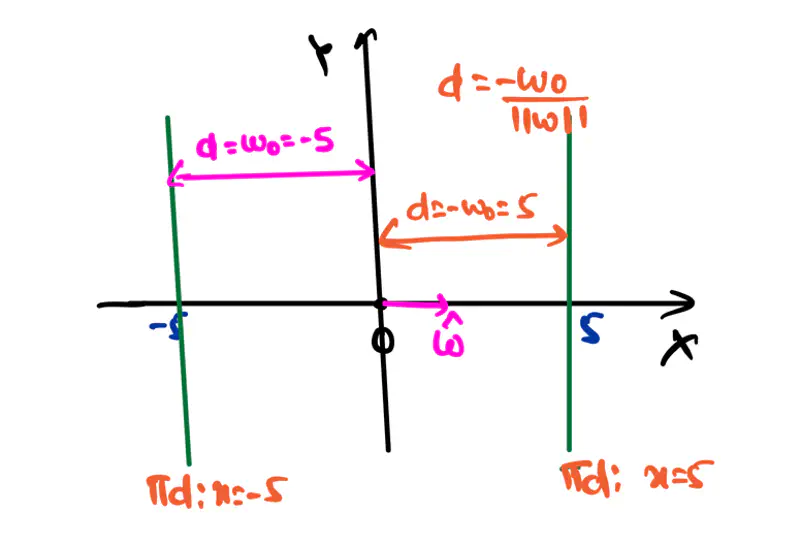
Let, the equation of the line/hyperplane in 2D be:
\(\pi_d = 1.x + 0.y + w_0 = x + w_0 = 0\)

Case 1: \(w_0 < 0\), say \(w_0 = -5\)
Therefore, equation of hyperplane: \( x - 5 = 0 => x = 5\)
Here, the hyperplane(line) is located in the same direction as the unit vector w.r.t the origin,
i.e, towards the +ve x-axis direction.

Case 2: \(w_0 > 0\), say \(w_0 = 5\)
Therefore, equation of hyperplane: \( x + 5 = 0 => x = -5\)
Here, the hyperplane(line) is located in the opposite direction as the unit vector w.r.t the origin,
i.e, towards the -ve x-axis direction.

images/maths/linear_algebra/hyperplane_example.png

Half Spaces

A hyperplane divides a space into 2 distinct parts called half-spaces.
e.g.: A 2D hyperplane divided a 3D space into 2 distinct parts.
Similar example in real world: A wall divides a room into 2 distinct spaces.

Positive Half-Space:
A half space that is in the same direction as the unit vector w.r.t the origin.

Negative Half-Space:
A half space that is in the opposite direction as the unit vector w.r.t the origin.

\[ \text { If point 'x' is on the hyperplane, then:} \\[10pt] \pi_d = \mathbf{w}^\top \mathbf{x} + w_0 = 0 \\[10pt] \mathbf{w}^\top \mathbf{x_1} + w_0 > 0 ~or~ \mathbf{w}^\top \mathbf{x_1} + w_0 < 0 \quad ? \\[10pt] \text { Distance of } x_1 < x_1\prime \text{ as } x_1 \text{ is between the origin and the hyperplane and } x_1\prime \text { lies on the hyperplane } \\[10pt] => \tag{1}\Vert \mathbf{x_1} \Vert < \Vert \mathbf{x_1\prime} \Vert \]

\[ \mathbf{w}^\top \mathbf{x_1\prime} + w_0 = 0 \\[10pt] => \tag{2} \Vert \mathbf{w} \Vert \Vert \mathbf{x_1\prime} \Vert cos{\theta} + w_0 = 0 \]

from equations (1) & (2), we can say that:

\[ \Vert \mathbf{w} \Vert \Vert \mathbf{x_1} \Vert cos{\theta} + w_0 < \Vert \mathbf{w} \Vert \Vert \mathbf{x_1\prime} \Vert cos{\theta} + w_0 \]

Everything is same on both the sides except \(\Vert \mathbf{x_1}\Vert\) and \(\Vert \mathbf{x_1\prime\Vert}\), so:

\[ \mathbf{w}^\top \mathbf{x_1} + w_0 < 0 \]

i.e, negative half-space, opposite to the direction of unit vector or towards the origin.
Similarly,

\[ \mathbf{w}^\top \mathbf{x_2} + w_0 > 0 \]

i.e, positive half-space, same as the direction of unit vector or away from the origin.

Equation of distance of any point \(x\prime\) from the hyperplane:

\[ d_{\pi_d} = \frac{\mathbf{w}^\top \mathbf{x\prime} + w_0}{\Vert \mathbf{w}\Vert} = 0 \]
images/maths/linear_algebra/half_spaces.png
Applications of Equation of Hyperplane

The above concept of equation of hyperplane will be very helpful when we discuss the following topics later:

  1. Logistic Regression
  2. Support Vector Machines

Equation of a Hyperplane for Machine Learning | Half Spaces | Explained with Example


End of Section