Conditional Probability

Conditional Probability & Bayes Theorem

  3 minute read  

In this section, we will understand all the concepts related to Conditional Probability and Bayes’ Theorem.


📘

Conditional Probability:
It is the probability of an event occurring, given that another event has already occurred.
Allows us to update probability when additional information is revealed.

\[P(A \mid B) = \frac{P(A \cap B)}{P(B)}\]

📘 Chain Rule:
\(P(A \cap B) = P(B)*P(A \mid B)\) or
\(P(A \cap B) = P(A)*P(B \mid A)\)

For example:

  1. Roll a die, sample space: \(\Omega = \{1,2,3,4,5,6\}\)
    Event A = Get a 5 = \(\{5\} => P(A) = 1/6\)
    Event B = Get an odd number = \(\{1, 3, 5\} => P(B) = 3/6 = 1/2\)
$$ \begin{aligned} \because (A \cap B) = \{5\} ~ => P(A \cap B) = 1/6 \\ P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\ &= \frac{1/6}{1/2} \\ &= 1/3 \end{aligned} $$


📘

Bayes’ Theorem:
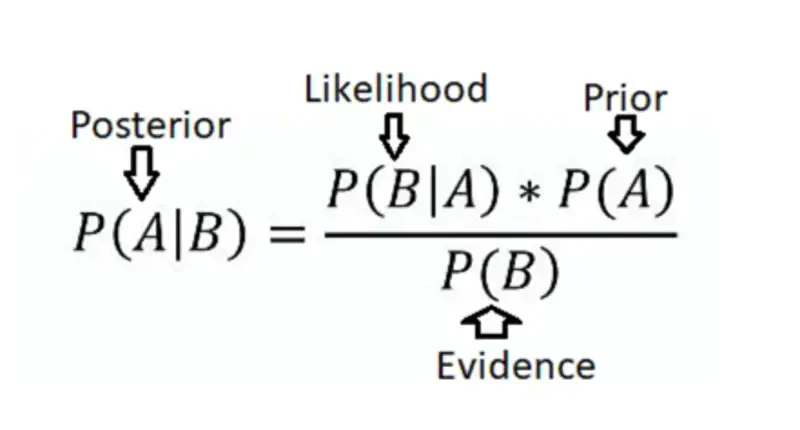
It is a formula that uses conditional probability.
It allows us to update our belief about an event’s probability based on new evidence.
We know from conditional probability and chain rule that:

$$ \begin{aligned} P(A \cap B) = P(B)*P(A \mid B) \\ P(A \cap B) = P(A)*P(B \mid A) \\ P(A \mid B) = \frac{P(A \cap B)}{P(B)} \end{aligned} $$

Combining all the above equations gives us the Bayes’ Theorem:

$$ \begin{aligned} P(A \mid B) = \frac{P(A)*P(B \mid A)}{P(B)} \end{aligned} $$


For example:

  1. Roll a die, sample space: \(\Omega = \{1,2,3,4,5,6\}\)
    Event A = Get a 5 = \(\{5\} => P(A) = 1/6\)
    Event B = Get an odd number = \(\{1, 3, 5\} => P(B) = 3/6 = 1/2\)
    Task: Find the probability of getting a 5 given that you rolled an odd number.

\(P(B \mid A) = 1\) = Probability of getting an odd number given that we have rolled a 5.

$$ \begin{aligned} P(A \mid B) &= \frac{P(A) * P(B \mid A)}{P(B)} \\ &= \frac{1/6 * 1}{1/2} \\ &= 1/3 \end{aligned} $$

Now, let’s understand another concept called Law of Total Probability.
Here, we can say that the sample space \(\Omega\) is divided into 2 parts - \(A\) and \(A ^ \complement \)

So, the probability of an event \(B\) is given by:

$$ B = B \cap A + B \cap A ^ \complement \\ P(B) = P(B \cap A) + P(B \cap A ^ \complement ) \\ By ~Chain ~Rule: P(B) = P(A)*P(B \mid A) + P(A ^ \complement )*P(B \mid A ^ \complement ) $$


💡 What if the sample space is divided into ’n’ such partitions ?

📘

Law of Total Probability:
Overall probability of an event B, considering all the different, mutually exclusive ways it can occur.
If A₁, A₂, …, Aₙ are a set of events that partition the sample space, such that they are -

  • Mututally exclusive : \(A_i \cap A_j = \emptyset\) for all \(i, j\)
  • Exhaustive: \(A₁ \cup A₂ ... \cup Aₙ = \Omega\) for all \(i \neq j\) $$ P(B) = \sum_{i=1}^{n} P(A_i)*P(B \mid A_i) $$ where \(n\) is the number of mutually exclusive partitions of the sample space \(\Omega\) .

Now, we can also generalize the Bayes’ Theorem using the Law of Total Probability.


End of Section