Independence of Events

Independence of Events

  3 minute read  

In this section, we will understand different kinds of Independence of Events.

📘

Independence of Events:
Two events are independent if the occurrence of one event does not affect the probability of the other event.
There are 3 types of independence of events:

  • Mutual Independence
  • Pair-Wise Independence
  • Conditional Independence

📘

Mutual Independence:
Joint probability of two events is equal to the product of the individual probabilities of the two events.
\(P(A \cap B) = P(A)*P(B)\)

Joint probability: The probability of two or more events occurring simultaneously.
\(P(A \cap B)\) or \(P(A, B)\)

For example:

  1. Toss a coin and roll a die -
    \(A\) = Get a heads; \(P(A)=1/2\)
    \(B\) = Get an odd number; \(P(B)=1/2\)
$$ \begin{aligned} P(A \cap B) &= P(\text{Heads and Odd}) \\ &= \frac{1}{2} * \frac{1}{2} \\ &= \frac{1}{4} \\ \\ \text{also } P(A) * P(B) &= \frac{1}{2} * \frac{1}{2} \\ &= \frac{1}{4} \end{aligned} $$
=> A and B are mutually independent.

📘 Pair-Wise Independence:
Every pair of events in the set is independent.
Pair-wise independence != Mutual independence.

For example:

  1. Toss 3 coins;
    For 2 tosses, sample space: \(\Omega = \{HH,HT, TH, TT\}\)
    \(A\) = First and Second toss outcomes are same i.e \(\{HH, TT\}\); \(P(A)= 2/4 = 1/2\)
    \(B\) = Second and Third toss outcomes are same i.e \(\{HH, TT\}\); \(P(B)= 2/4 = 1/2\)
    \(C\) = Third and First toss outcomes are same i.e \(\{HH, TT\}\); \(P(C)= 2/4 = 1/2\)

Now, pair-wise independence of the above events A & B is - \(P(A \cap B)\)
\(P(A \cap B)\) => Outcomes of first and second toss are same &
outcomes of second and third toss are same.
=> Outcomes of all the three tosses are same.

Total number of outcomes = 8
Desired outcomes = \(\{HHH, TTT\}\) = 2
=> \(P(A \cap B) = 2/8 = 1/4 = P(A) * P(B) = 1/2 * 1/2 = 1/4\)

Therefore, \(A\) and \(B\) are pair-wise independent.
Similarly, we can also prove that \(A\) and \(C\) and \(B\) and \(C\) are also pair-wise independent.

Now, let’s check for mutual independence of the above events A, B & C.
\(P(A \cap B \cap C) = P(A)*P(B)*P(C)\)
\(P(A \cap B \cap C)\) = Outcomes of all the three tosses are same i.e \(\{HHH, TTT\}\)
Total number of outcomes = 8
Desired outcomes = \(\{HHH, TTT\}\) = 2
So, \(P(A \cap B \cap C)\) = 2/8 = 1/4
But, \(P(A)*P(B)*P(C) = 1/2*1/2*1/2 = 1/8\)
Therefore \(P(A \cap B \cap C)\) ≠ \(P(A)*P(B)*P(C)\)
=> \(A, B, C\) are NOT mutually independent but only pair wise independent.

📘 Conditional Independence:
Two events A & B are conditionally independent given a third event C,
if they are independent given that C has occurred.
Occurrence of C changes the context, causing the events A & B to become independent of each other.


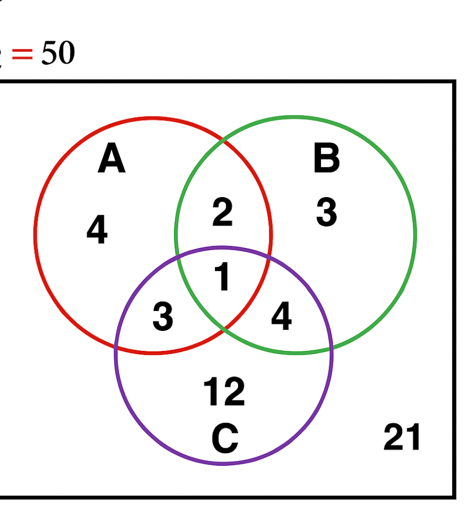
$$ \begin{aligned} A = 10 ,~ B = 10 ,~ C = 20 ~and~ \Omega = 50 \\ P(A) = 10/50 = 1/5 \\ P(B) = 10/50 = 1/5 \\ P(A) * P(B) = 1/5*1/5 =1/25 \\ P(A \cap B) = 3/50 \\ \text{clearly, } P(A \cap B) ~⍯ ~P(A) * P(B) \\ \end{aligned} $$

=> A & B are NOT independent.
Now, let’s check for conditional independence of A & B given C.

$$ \begin{aligned} P(A \mid C) &= \frac{P(A \cap C)}{P(C)} = 4/20 = 1/5 \\ P(B \mid C) &= \frac{P(B \cap C)}{P(C)} = 5/20 = 1/4 \\ P(A \mid C) * P(B \mid C) &= 1/5 * 1/4 = 1/20 \\ P(A \cap B \mid C) &= \frac{P(A \cap B \cap C)}{P(C)} = 1/20 \\ \text{clearly, } P(A \cap B \mid C) &= P(A \mid C)*P(B \mid C) \\ \end{aligned} $$

Therefore, A & B are conditionally independent given C.


End of Section