Joint & Marginal

Joint, Marginal & Conditional Probability

  7 minute read  

In this section, we will understand Joint, Marginal & Conditional Probability.
So far, we have dealt with a single random variable.
Now, let’s explore the probability distributions of 2 or more random variables occurring together.


📘

Joint Probability Distribution:
It describes the probability of 2 or more random variables occurring simultaneously.

  • The random variables can be from different distributions, such as, discrete and continuous.

Joint CDF:

\[ F_{X,Y}(a,b) = P(X \le a, Y \le b),~ -\infty < a, b < \infty \]

Discrete Case:

\[ F_{X,Y}(a,b) = P(X \le a, Y \le b) = \sum_{x_i \le a} \sum_{y_j \le b} P(X = x_i, Y = y_j) \]

Continuous Case:

\[ F_{X,Y}(a,b) = P(X \le a, Y \le b) = \int_{-\infty}^{a} \int_{-\infty}^{b} f_{X,Y}(x,y) dy dx \]

Joint PMF:

\[ P_{X,Y}(x,y) = P(X = x, Y = y) \]

Key Properties:

  1. \(P(X = x, Y = y) \ge 0 ~ \forall (x,y) \)
  2. \( \sum_{i} \sum_{j} P(X = x_i, Y = y_j) = 1 \)

Joint PDF:

\[ f_{X,Y}(x,y) = \frac{\partial^2 F_{X,Y}(x,y)}{\partial x \partial y} \\ f_{X,Y}(x,y) = \iint_{A \in \mathbb{R}^2} f_{X,Y}(x,y) dy dx \]

Key Properties:

  1. \(f_{X,Y}(x,y) \ge 0 ~ \forall (x,y) \)
  2. \( \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f_{X,Y}(x,y) dy dx = 1 \)
For example:

  • If we consider 2 random variables, say, height(X) and weight(Y), then the joint distribution will tell us the probability of finding a person having a particular height and weight.

💡 There are 2 bags; bag_1 has 2 red balls & 3 blue balls, bag_2 has 3 red balls & 2 blue balls.
A ball is picked at random from each bag, such that both draws are independent of each other.
Let’s use this example to understand joint probability.


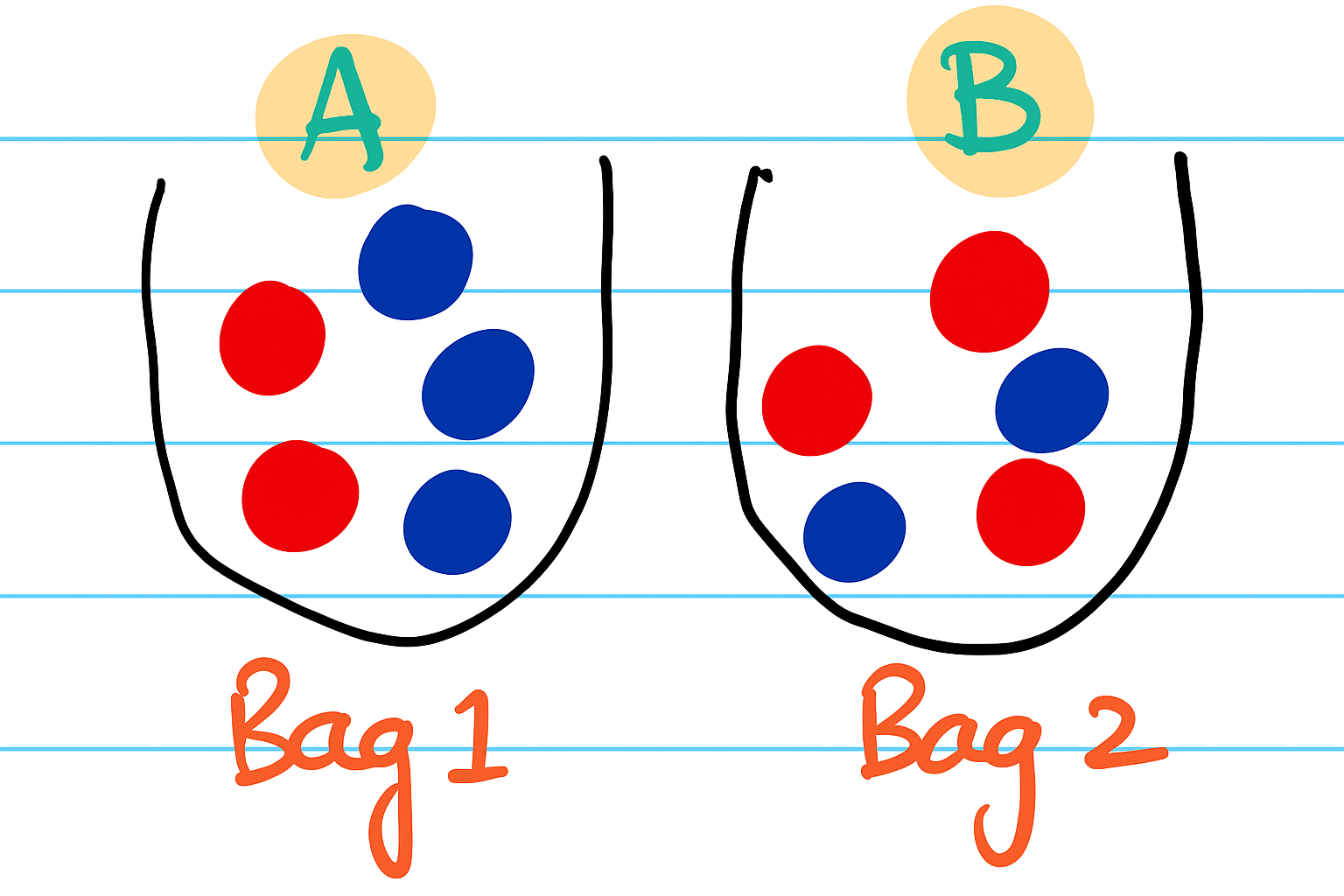
Let A & B be discrete random variables associated with the outcome of the ball drawn from first and second bags respectively.

A = RedA = Blue
B = Red2/5*3/5 = 6/253/5*3/5 = 9/25
B = Blue2/5*2/5 = 4/253/5*2/5 = 6/25

Since, the draws are independent, joint probability = P(A) * P(B)
Each of the 4 cells in above table shows the probability of combination of results from 2 draws or joint probability.



📘

Marginal Probability Distribution:
It describes the probability distribution of an individual random variable in a joint distribution, without considering the outcomes of other random variables.

  • If we have the joint distribution, then we can get the marginal distribution of each random variable from it.
  • Marginal probability equals summing the joint probability across other random variables.

Marginal CDF:
We know that Joint CDF =

\[ F_{X,Y}(a,b) = P(X \le a, Y \le b),~ -\infty < a, b < \infty \]

Marginal CDF =

\[ F_X(a, \infty) = P(X \le a, Y < \infty) = P(X \le a) \]

Discrete Case:

\[ F_X(a) = P(X \le a, Y \le \infty) = \sum_{x_i \le a} \sum_{y_j \in \mathbb{R}} P(X = x_i, Y = y_j) \]

Continuous Case:

\[ F_X(a) = P(X \le a, Y \le \infty) = \int_{-\infty}^{a} \int_{-\infty}^{\infty} f_{X,Y}(x,y)dydx = \int_{-\infty}^{\infty} f_{X,Y}(x,y)dy \]

Law of Total Probability
We know that Joint Probability Distribution =

\[ P_{X,Y}(x,y) = P(X = x, Y = y) \]

The events \((Y=y)\) partition the sample space, such that:

  1. \( (Y=y_1) \cap (Y=y_2) \cap ... \cap (Y=y_n) = \Phi \)
  2. \( (Y=y_1) \cup (Y=y_2) \cup ... \cup (Y=y_n) = \Omega \)

From Law of Total Probability, we get:

Marginal PMF:

\[ P_X(x) = P(X=x) = \sum_{y} P_{X,Y}(x,y) = \sum_{y} P(X = x, Y = y) \]

Marginal PDF:

\[ f_X(x) = \int_{-\infty}^{\infty} f_{X,Y}(x,y) dy \]


💡 Setup: Roll a die + Toss a coin.
X: Roll a die ; \( \Omega = \{1,2,3,4,5,6\} \)
Y: Toss a coin ; \( \Omega = \{H,T\} \)

Joint PMF = \( P_{X,Y}(x,y) = P(X=x, Y=y) = 1/6*1/2 = 1/12\)
Marginal PMF of X = \( P_X(x) =\sum_{y \in \mathbb{\{H,T\}}} P_{X,Y}(x,y) = = 1/12+1/12 = 1/6\)
=> Marginally, X is uniform over 1-6 i.e a fair die.

Marginal PMF of Y = \( P_Y(y) = \sum_{1}^6 P_{X,Y}(x,y) = 6*(1/12) = 1/2 \)
=> Marginally, Y is uniform over H,T i.e a fair coin.

💡 Setup: X and Y are two continuous uniform distribution.
\( X \sim U(0,1) \)
\( Y \sim U(0,1) \)

Marginal PDF = \(f_X(x) = \int_{-\infty}^{\infty} f_{X,Y}(x,y) dy \)
Joint PDF =

$$ f_{X,Y}(x,y) = \begin{cases} 1 & \text{if } x \in [0,1], y \in [0,1] \\ 0 & \text{otherwise } \end{cases} $$

Marginal PDF =

\[ \begin{aligned} f_X(x) &= \int_{0}^{1} f_{X,Y}(x,y) dy \\ &= \int_{0}^{1} 1 dy \\ &= 1 \\ f_X(x) &= \begin{cases} 1 & \text{if } x \in [0,1] \\ 0 & \text{otherwise } \end{cases} \end{aligned} \]

💡 Let’s re-visit the ball drawing example.
There are 2 bags; bag_1 has 2 red balls & 3 blue balls, bag_2 has 3 red balls & 2 blue balls.
A ball is picked at random from each bag, such that both draws are independent of each other.
Let’s use this example to understand marginal probability.


Let A & B be discrete random variables associated with the outcome of the ball drawn from first and second bags respectively.

A = RedA = BlueP(B) (Marginal)
B = Red2/5*3/5 = 6/253/5*3/5 = 9/256/25 + 9/25 = 15/25 = 3/5
B = Blue2/5*2/5 = 4/253/5*2/5 = 6/254/25 + 6/25 = 10/25 = 2/5
P(A) (Marginal)6/25 + 4/25 = 10/25 = 2/59/25 + 6/25 = 15/25 = 3/5

We can see from the table above - P(A=Red) is the sum of joint distribution over all possible values of B i.e Red & Blue.



📘

Conditional Probability:
It measures the probability of an event occurring given that another event has already happened.

  • It provides a way to update our belief about the likelihood based on new information.
\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)} \]

P(A, B) = Joint Probability of A and B
P(B) = Marginal Probability of B

=> Conditional Probability = Joint Probability / Marginal Probability

Conditional CDF:

\[ F_{X \mid Y}(x \mid y) = P(X \le x \mid Y = y) \\ \]

Discrete Case:

\[ F_{X \mid Y}(x \mid y) = P(X \le x \mid Y = y) = \sum_{x_i \le x} P(X = x_i \mid Y = y) \]

Continuous Case:

\[ F_{X \mid Y}(x \mid y) = \int_{-\infty}^{x} f_{X \mid Y}(x \mid y) dx = \int_{-\infty}^{x} \frac {f_{X,Y}(x, y)}{f_Y(y)} dx \\ f_Y(y) > 0 \]

Conditional PMF:

\[ P(X = x \mid Y = y) = \frac{P(X = x, Y = y)} {P(Y = y)} \\ P(Y = y) > 0 \]

Conditional PDF:

\[ f_{X \mid Y}(x \mid y) = \frac{F_{X,Y}(x,y)}{f_Y(y)} \\ f_Y(y) > 0 \]

Application:

  • Generative machine learning models, such as, GANs, learn the conditional distribution of pixels, given the style of input image.

💡 Let’s re-visit the ball drawing example.
Note: We only have information about the joint and marginal probabilities.
What is the conditional probability of drawing a red ball in the first draw, given that a blue ball is drawn in second draw?


Let A & B be discrete random variables associated with the outcome of the ball drawn from first and second bags respectively.
A = Red ball in first draw
B = Blue ball in second draw.

A = RedA = BlueP(B) (Marginal)
B = Red6/259/253/5
B = Blue4/256/252/5
P(A) (Marginal)2/53/5
\[ \begin{aligned} P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\ &= \frac{4/25}{2/5} \\ &= 2/5 \end{aligned} \]

Therefore, probability of drawing a red ball in the first draw, given that a blue ball is drawn in second draw = 2/5.



📘

Conditional Expectation:
This gives us the conditional expectation of a random variable X, given another random variable Y=y.

Discrete Case:

\[ E[X \mid Y = y] = \sum_{x} x.P(X = x \mid Y = y) x = \sum_{x} x.P_{X \mid Y}(x \mid y) \]

Continuous Case:

\[ E[X \mid Y = y] = \int_{-\infty}^{\infty} x.f_{X \mid Y}(x \mid y) dx \]

For example:

  • Conditional expectation of of a person’s weight, given his/her height = 165 cm, will give us the average weight of all people with height = 165 cm.

Applications:

  • Linear regression algorithm is conditional expectation of target variable ‘Y’, given input feature variable ‘X’.
  • Expectation Maximisation(EM) algorithm is built on conditional expectation.

📘

Conditional Variance:
This gives us the variance of a random variable calculated after taking into account the value(s) of another related variable.

\[ \begin{aligned} Var[X \mid Y = y] &= \sum_{x} [x - E[X \mid Y = y])^2 \mid Y=y] \\ => Var[X \mid Y = y] &= E[X^2 \mid Y=y] - (E[X \mid Y=y])^2 \\ \end{aligned} \]

For example:

  • Variance of car’s mileage for city driving might be small, but the variance will be large for mix of city and highway driving.

Note: Models that take into account the change in variance or heteroscedasticity tend to be more accurate.



End of Section