Probability Mass Function
4 minute read
It assigns a “non-zero” mass or probability to a specific countable outcome.
Note: Called ‘mass’ because probability is concentrated at a single discrete point.
\(PMF = P(X=x)\)
e.g: Bernoulli, Binomial, Multinomial, Poisson etc.
Commonly visualised as a bar chart.
Note: PMF = Jump at a given point in CDF.
\(PMF = P_x(X=x_i) = F_X(X=x_i) - F_X(X=x_{i-1})\)
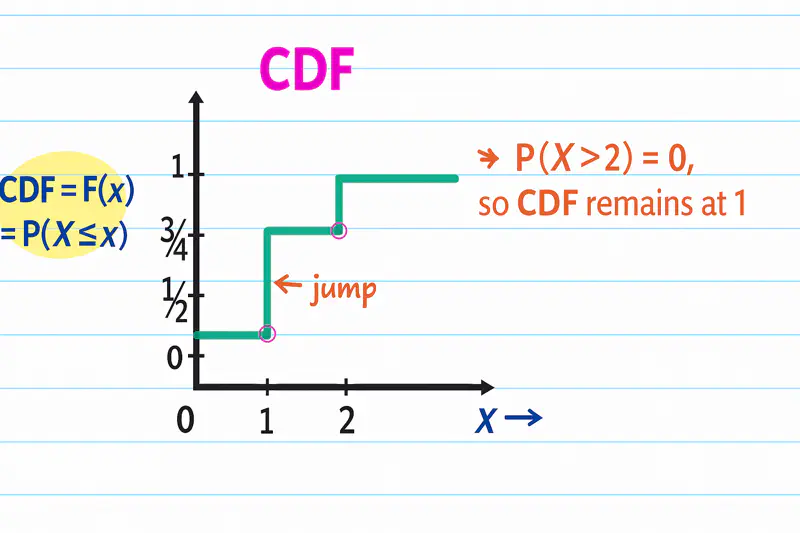
- Non-Negative: Probability of any value ‘x’ must be non-negative i.e \(P(X=x) \ge 0 ~\forall x~\).
- Sum = 1: Sum of probabilities of all possible outcomes must be 1.
\( \sum_{x} P(X=x) = 1 \) - For any value that the discrete random variable can NOT take, the probability must be zero.
p = Probability of success
1-p = Probability of failure
Mean = p
Variance = p(1-p)
Note: A single trial that adheres to these conditions is called a Bernoulli trial.
\(PMF, P(x) = p^x(1-p)^{1-x}\), where \(x \in \{0,1\}\)
- Toss a coin, we get heads or tails.
- Result of a test, pass or fail.
- Machine learning, binary classification model.
It extends the Bernoulli distribution by modeling the number of successes that occur over a fixed number of
independent trials.
n = Number of trials
k = Number of successes
p = Probability of success
Mean = np
Variance = np(1-p)
\(PMF, P(x=k) = \binom{n}{k}p^k(1-p)^{n-k}\), where \(k \in \{0,1,2,3,...,n\}\)
\(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) i.e number of ways to achieve ‘k’ successes in ‘n’ independent trials.
Note: Bernoulli is a special case of Binomial distribution where n = 1.
Also read about Multinomial distribution i.e where number of possible outcomes is > 2.
- Counting number of heads(success) in ’n’ coin tosses.
- Trials are independent.
- Probability of success remains constant for every trial.
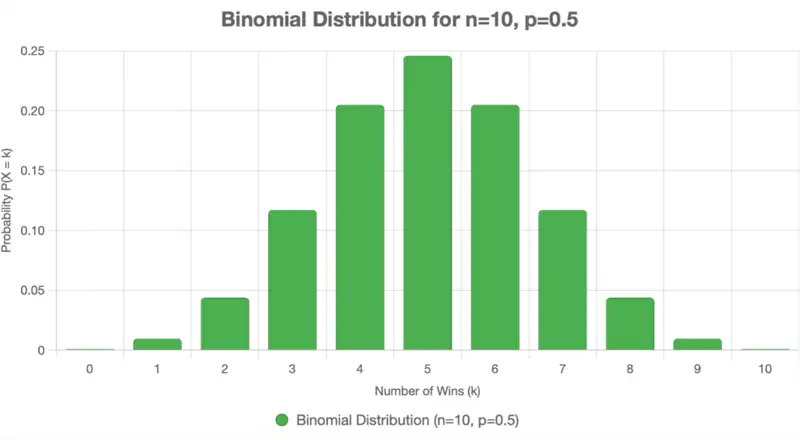
Total number of outcomes in 3 coin tosses = 2^3 = 8
Desired outcomes i.e 2 heads in 3 coin tosses = \(\{HHT, HTH, THH\}\) = 3
Probability of getting exactly 2 heads in 3 coin tosses = \(\frac{3}{8}\) = 0.375
Now lets solve the question using the binomial distribution formula.
Number of successes, k = 1
Number of trials, n = 10
Probability of success, p = 1/3
Probability of winning lottery, P(k=1) =
It expresses the probability of an event happening a certain number of times ‘k’ within a fixed interval of time.
Given that:
- Events occur with a known constant average rate.
- Occurrence of an event is independent of the time since the last event.
Parameters:
\(\lambda\): Expected number of events per interval
\(k\) = Number of events in the same interval
Mean = \(\lambda\)
Variance = \(\lambda\)
PMF = Probability of occurrence of ‘k’ events in the same interval
Note: Useful to count data where total population size is large but the probability of an individual event is small.
- Model the number of customers arrival at a service center per hour.
- Number of website clicks in a given time period.
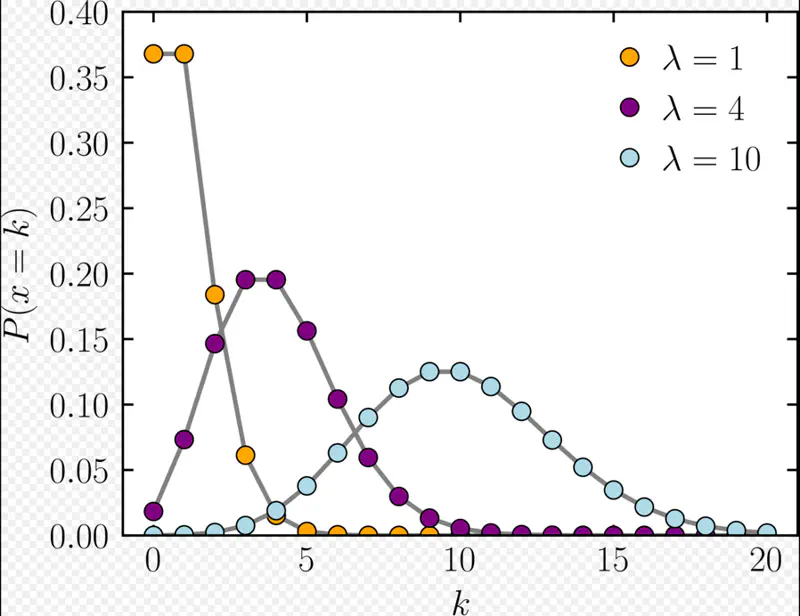
Expected (average) number of emails per hour, \(\lambda\) = 5
Probability of receiving exactly k=3 emails in the next hour =
End of Section