Probability Mass Function
Probability Mass Function of a Discrete Random Variable
4 minute read
In this section, we will understand Probability Mass Function of a Discrete Random Variable.
📘 Probability Mass Function(PMF):
It gives the exact value of a probability for a discrete random variable at a specific value \(x\).
It assigns a “non-zero” mass or probability to a specific countable outcome.
Note: Called ‘mass’ because probability is concentrated at a single discrete point.
\(PMF = P(X=x)\)
e.g: Bernoulli, Binomial, Multinomial, Poisson etc.
Commonly visualised as a bar chart.
Note: PMF = Jump at a given point in CDF.
\(PMF = P_x(X=x_i) = F_X(X=x_i) - F_X(X=x_{i-1})\)
It gives the exact value of a probability for a discrete random variable at a specific value \(x\).
It assigns a “non-zero” mass or probability to a specific countable outcome.
Note: Called ‘mass’ because probability is concentrated at a single discrete point.
\(PMF = P(X=x)\)
e.g: Bernoulli, Binomial, Multinomial, Poisson etc.
Commonly visualised as a bar chart.
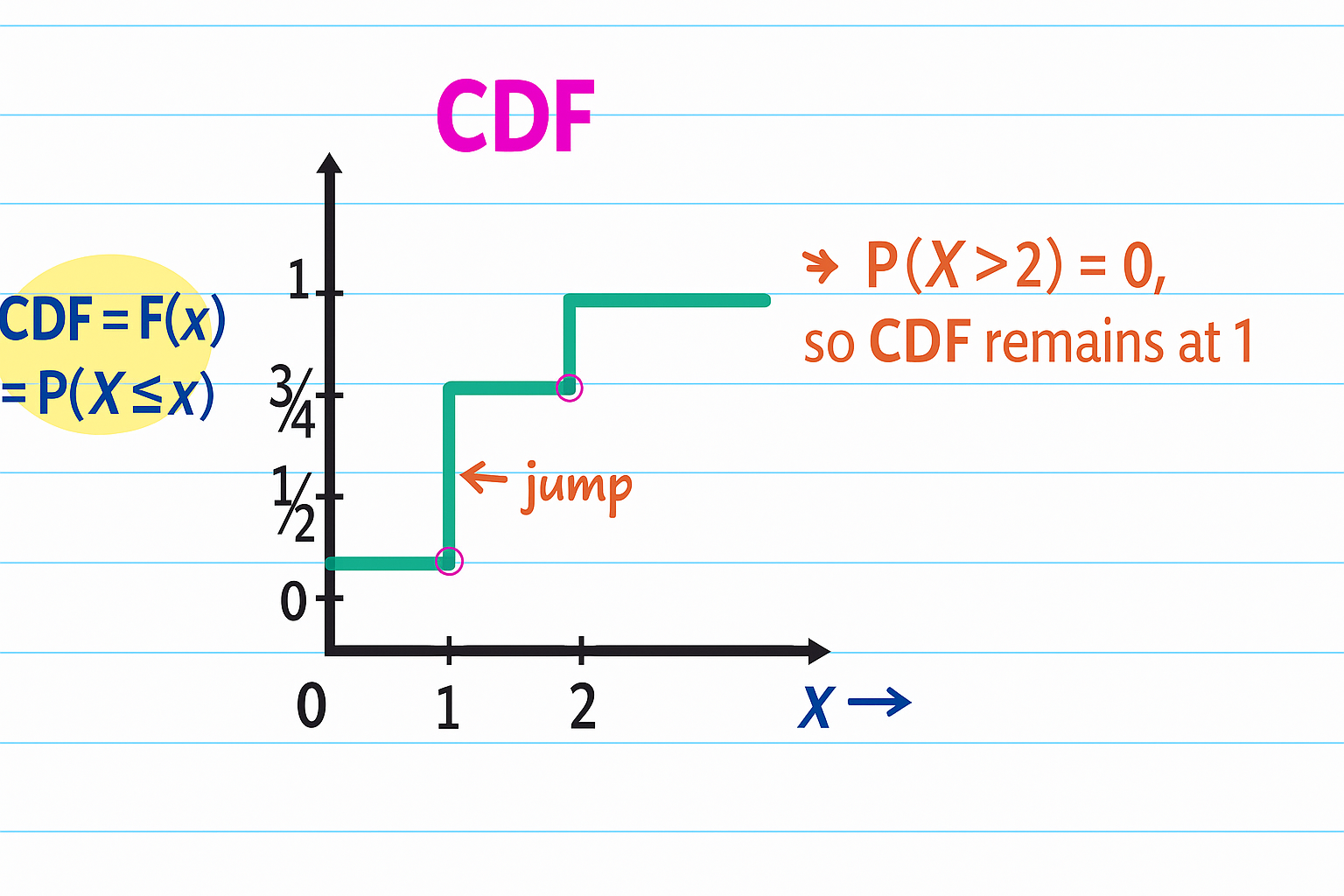
Note: PMF = Jump at a given point in CDF.
\(PMF = P_x(X=x_i) = F_X(X=x_i) - F_X(X=x_{i-1})\)
Key properties of PMF
- Non-Negative: Probability of any value ‘x’ must be non-negative i.e \(P(X=x) \ge 0 ~\forall x~\).
- Sum = 1: Sum of probabilities of all possible outcomes must be 1.
\( \sum_{x} P(X=x) = 1 \) - For any value that the discrete random variable can NOT take, the probability must be zero.
📘 Bernoulli Distribution:
It models a single event with two possible outcomes, success (1) or failure (0), with a fixed probability of success, ‘p’.
p = Probability of success
1-p = Probability of failure
Mean = p
Variance = p(1-p)
Note: A single trial that adheres to these conditions is called a Bernoulli trial.
\(PMF, P(x) = p^x(1-p)^{1-x}\), where \(x \in \{0,1\}\)
For example:It models a single event with two possible outcomes, success (1) or failure (0), with a fixed probability of success, ‘p’.
p = Probability of success
1-p = Probability of failure
Mean = p
Variance = p(1-p)
Note: A single trial that adheres to these conditions is called a Bernoulli trial.
\(PMF, P(x) = p^x(1-p)^{1-x}\), where \(x \in \{0,1\}\)
- Toss a coin, we get heads or tails.
- Result of a test, pass or fail.
- Machine learning, binary classification model.
📘
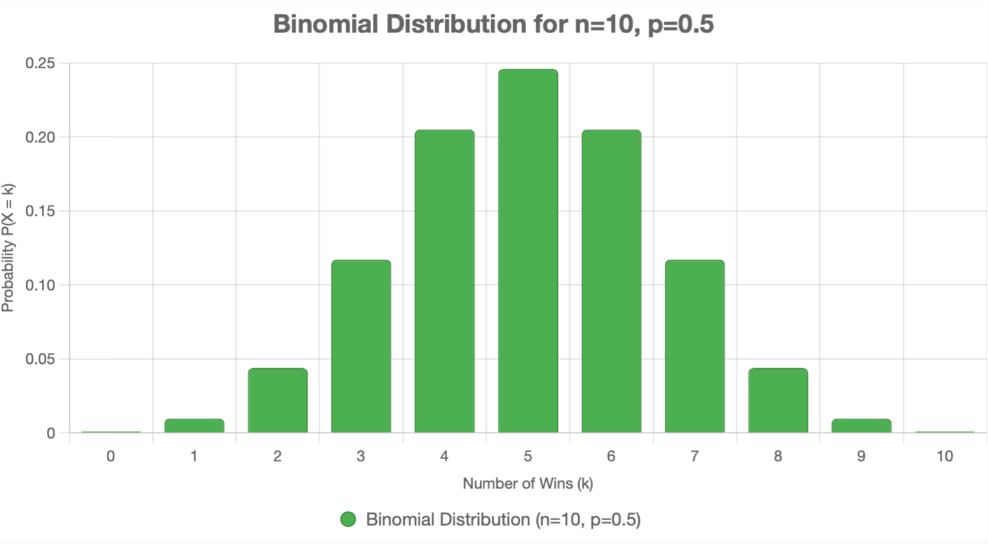
For example:Binomial Distribution:
It extends the Bernoulli distribution by modeling the number of successes that occur over a fixed number of
independent trials.
n = Number of trials
k = Number of successes
p = Probability of success
Mean = np
Variance = np(1-p)
\(PMF, P(x=k) = \binom{n}{k}p^k(1-p)^{n-k}\), where \(k \in \{0,1,2,3,...,n\}\)
\(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) i.e number of ways to achieve ‘k’ successes in ‘n’ independent trials.
Note: Bernoulli is a special case of Binomial distribution where n = 1.
- Counting number of heads(success) in ’n’ coin tosses.
Assumptions
- Trials are independent.
- Probability of success remains constant for every trial.
💡 What is the probability of getting exactly 2 heads in 3 coin tosses?
Total number of outcomes in 3 coin tosses = 2^3 = 8
Desired outcomes i.e 2 heads in 3 coin tosses = \(\{HHT, HTH, THH\}\) = 3
Probability of getting exactly 2 heads in 3 coin tosses = \(\frac{3}{8}\) = 0.375
Now lets solve the question using the binomial distribution formula.
\(P(k=2) = \binom{3}{2}p^2(1-p)^{3-2} = \frac{3!}{2!(3-2)!}(0.5)^2(0.5) = 3*0.25*0.5 = 3*0.125 = 0.375\)
Desired outcomes i.e 2 heads in 3 coin tosses = \(\{HHT, HTH, THH\}\) = 3
Probability of getting exactly 2 heads in 3 coin tosses = \(\frac{3}{8}\) = 0.375
Now lets solve the question using the binomial distribution formula.
\(P(k=2) = \binom{3}{2}p^2(1-p)^{3-2} = \frac{3!}{2!(3-2)!}(0.5)^2(0.5) = 3*0.25*0.5 = 3*0.125 = 0.375\)
💡 What is the probability of winning a lottery 1 out of 10 times, given that the probability of winning a single lottery
= 1/3?
Number of successes, k = 1
Number of trials, n = 10
Probability of success, p = 1/3
Probability of winning lottery, P(k=1) = \(\binom{10}{1}p^1(1-p)^{10-1} = \frac{10!}{1!(10-1)!}(1/3)^1(2/3)^9 = 10*0.333*0.026 = 0.866 \approx 8.66\% \)
Number of trials, n = 10
Probability of success, p = 1/3
Probability of winning lottery, P(k=1) = \(\binom{10}{1}p^1(1-p)^{10-1} = \frac{10!}{1!(10-1)!}(1/3)^1(2/3)^9 = 10*0.333*0.026 = 0.866 \approx 8.66\% \)
📘
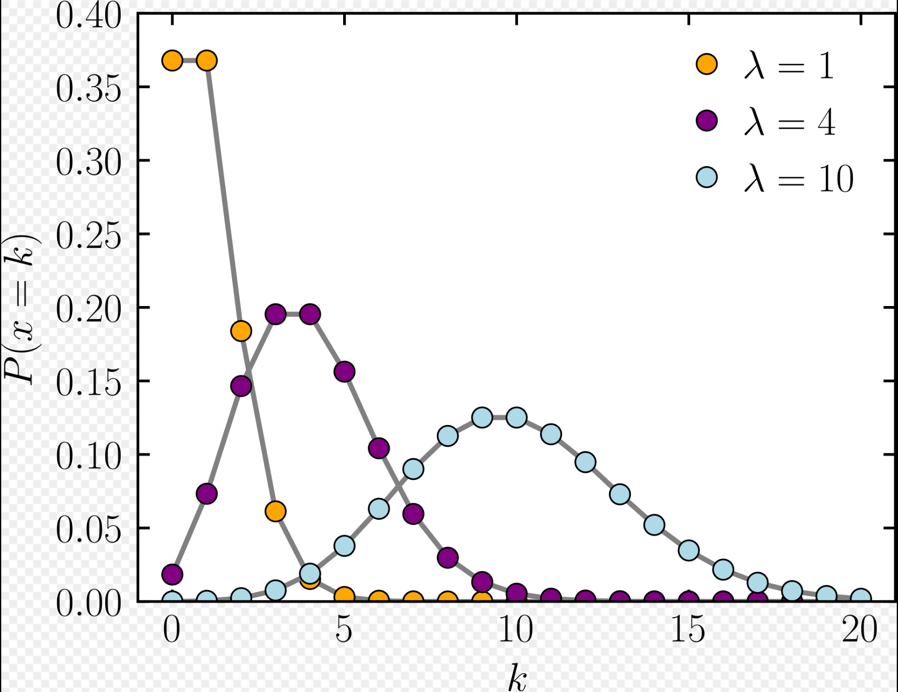
For example:Poisson Distribution:
It expresses the probability of an event happening a certain number of times ‘k’ within a fixed interval of time.
Given that:
- Events occur with a known constant rate.
- Occurrence of an event is independent of the time since the last event.
Parameters:
\(\lambda\): Expected number of events per interval
Mean = \(\lambda\)
Variance = \(\lambda\)
\(k\) = Number of events in the same interval
PMF = Probability of ‘k’ events in the same interval
\[PMF = \lambda^ke^{-\lambda}/k!\] Note: Useful to count data where total population size is large but the probability of an individual event is small.
- Model the number of customers arrival at a service center per hour.
- Number of website clicks in a given time period.
💡 A company receives, on an average, 5 customer emails per hour. What is the probability of receiving exactly 3 emails
in the next hour?
Expected (average) number of emails per hour, \(\lambda\) = 5
Probability of receiving exactly k=3 emails in the next hour = ?
\(P(k=3) = \lambda^3e^{-\lambda} / 3! = 5^3e^{-5} / 3! = 125*e^{-5} / 6 = 125*0.00674 / 6 \approx 0.14 ~or~ 14\% \)
Probability of receiving exactly k=3 emails in the next hour = ?
\(P(k=3) = \lambda^3e^{-\lambda} / 3! = 5^3e^{-5} / 3! = 125*e^{-5} / 6 = 125*0.00674 / 6 \approx 0.14 ~or~ 14\% \)
End of Section