Hypothesis Testing

Hypothesis Testing

  8 minute read  

Hypothesis
An idea that is suggested as a possible explanation for a phenomenon, but has not been found to be true.
Why do we need Hypothesis Testing?

Hypothesis Testing is used to determine whether a claim or theory about a population is supported by a sample data,
by assessing whether observed difference or patterns are likely due to chance or represent a true effect.

  • It allows companies to test marketing campaigns or new strategies on a small scale before committing to larger investments.
  • Based on the results of hypothesis testing, we can make reliable inferences about the whole group based on a representative sample.
  • It helps us determine whether an observed result is statistically significant finding, or if it could have just happened by random chance.
Hypothesis Testing

It is a statistical inference framework used to make decisions about a population parameter, such as, the mean, variance, distribution, correlation, etc., based on a sample of data. It provides a formal method to evaluate competing claims.

Null Hypothesis (\(H_0\)):
Status quo or no-effect or no difference statement; almost always contains a statement of equality.

Alternative Hypothesis (\(H_1 ~or~ H_a\)):
The statement representing an effect, a difference, or a relationship.
It must be true if the null hypothesis is rejected.

Types of Hypothesis Testing
  1. Test of Means:
  • 1-Sample Mean Test: Compare sample mean to a known population mean.
  • 2-Sample Mean Test: Compare means of 2 populations.
  • Paired Mean Test: Compare means when data is paired, e.g., before vs. after test.
  1. Test of Median:
  • Mood’s Median Test
  • Sign Test
  • Wilcoxon Signed Rank Test (non-parametric)
  1. Test of Variance:
  • Chi-Square Test for a single variance
  • F-Test to compare variances of 2 populations
  1. Test of Distribution(Goodness of Fit):
  • Kolmogorov-Smirnov Test
  • Shapiro-Wilk Test
  • Anderson-Darling Test
  • Chi-Square Goodness of Fit Test
  1. Test of Correlation:
  • Pearson’s Correlation Coefficient Test
  • Spearman’s Rank Correlation Test
  • Kendall’s Tau Correlation Test
  • Chi-Square Test of Independence
  1. Regression Test:
  • T-Test: For regression coefficients
  • F-Test: For overall regression significance
Hypothesis Testing | Null Hypothesis | Alternate Hypothesis | Types of Hypothesis Test | Explained
Framework for Hypothesis Testing
We can structure any hypothesis test in 6 steps as follows:

Step 1: Define the null and alternative hypotheses.
Step 2: Select a relevant statistical test for the task with associated test statistic.
Step 3: Calculate the test statistic under null hypothesis.
Step 4: Select a significance level (\(\alpha\)), i.e, the maximum acceptable false positive rate;
typically - 5% or 1%.
Step 5: Compute the p-value from the observed value of test-statistic.
Step 6: Make a decision to either accept or reject the null hypothesis, based on the significance level (\(\alpha\)).
Perform a hypothesis test to compare the mean recovery time of 2 medicines.

Say, the data, D: <patient_id, med_1/med_2, recovery_time(in days)>
We need some metric to compare the recovery times of 2 medicines.
We can use the mean recovery time as the metric, because we know that we can use following techniques for comparison:

  1. 2-Sample T-Test; if \(n < 30\) and population standard deviation \(\sigma\) is unknown.
  2. 2-Sample Z-Test; if \(n \ge 30\) and population standard deviation \(\sigma\) is known.

Note: Let’s assume the sample size \(n < 30\), because medical tests usually have small sample sizes.
=> We will use the 2-Sample T-Test; we will continue using T-Test throughout the discussion.

Step 1: Define the null and alternative hypotheses.
Null Hypothesis \(H_0\): The mean recovery time of 2 medicines is the same i.e \(Mean_{m1} = Mean_{m2}\) or \(m_{m1} = m_{m2}\).
Alternate Hypothesis \(H_a\): \(m_{m1} < m_{m2}\) (1-Sided T-Test) or \(m_{m1} ⍯ m_{m2}\) (2-Sided T-Test).

Step 2: Select a relevant statistical test for the task with associated test statistic.
Let’s do a 2 sample T-Test, i.e, \(m_{m1} < m_{m2}\)

Step 3: Calculate the test statistic under null hypothesis.
Test Statistic:
For 2 sample T-Test:

\[t_{obs} = \frac{m_{m_1} - m_{m_2}}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]


s: Standard Deviation
n: Sample Size

Note: If the 2 means are very close then \(t_{obs} \approx 0\).

Step 4: Suppose significance level (\(\alpha\)) = 5% or 0.05.

Step 5: Compute the p-value from the observed value of test-statistic.
P-Value:

\[p_{value} = \mathbb{P}(t \geq t_{obs} | H_0)\]


p-value = area under curve = probability of observing test statistic \( \ge t_{obs} \) if the null hypothesis is true.

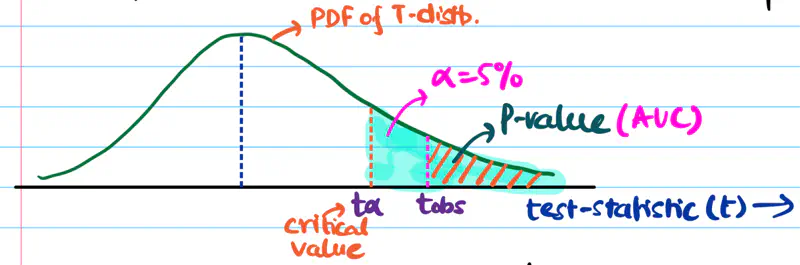
images/maths/statistics/p_value_1.png

Step 6: Accept or reject the null hypothesis, based on the significance level (\(\alpha\)).
If \(p_{value} < \alpha\), we reject the null hypothesis and accept the alternative hypothesis and vice versa.
Note: In the above example \(p_{value} < \alpha\), so we reject the null hypothesis.

Framework for Hypothesis Testing | Null & Alternate Hypothesis | P Value | Explained with Example
Left or Right Sided (Tailed) Test

We need to do a left or right sided test, or a 2-sided test, this depends upon our alternate hypothesis and test statistic.

Let’s continue our 2 sample mean T-test to understand the concept:

\[t_{obs} = \frac{m_{m_1} - m_{m_2}}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]

Left Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 < medicine 2, i.e, \(m_{m_1} < m_{m_2}\)
=> \(m_{m_1} - m_{m_2} < 0\)

\[t_{obs} = \frac{m_{m_1} - m_{m_2}}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]

Since, the denominator in above equation is always positive.
=> \(t_{obs} < 0\)
Therefore, we need to do a left sided/tailed test.

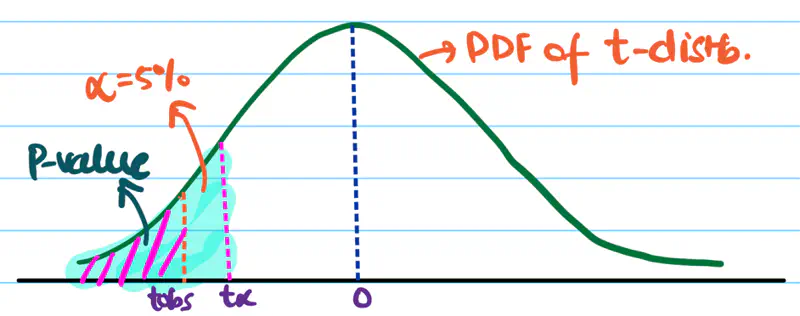
images/maths/statistics/left_tailed.png

So, we want \(t_{obs}\) to be very negative to confidently conclude that alternate hypothesis is true.

Right Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 > medicine 2, i.e, \(m_{m_1} > m_{m_2}\)
=> \(m_{m_1} - m_{m_2} > 0\)
Similarly, here we need to do a right sided/tailed test.

2 Sided/Tailed Test:
\(H_a\): Mean recovery time of medicine 1 ⍯ medicine 2, i.e, \(m_{m_1} ⍯ ~ m_{m_2}\)
=> \(m_{m_1} - m_{m_2} < 0\) or \(m_{m_1} - m_{m_2} > 0\)
If \(H_a\) is true then \(t_{obs}\) is a large -ve value or a large +ve value.

\[t_{obs} = \frac{m_{m_1} - m_{m_2}}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]

Since, t-distribution is symmetric, we can divide the significance level \(\alpha\) into 2 equal parts.
i.e \(\alpha = 2.5\%\) on each side.

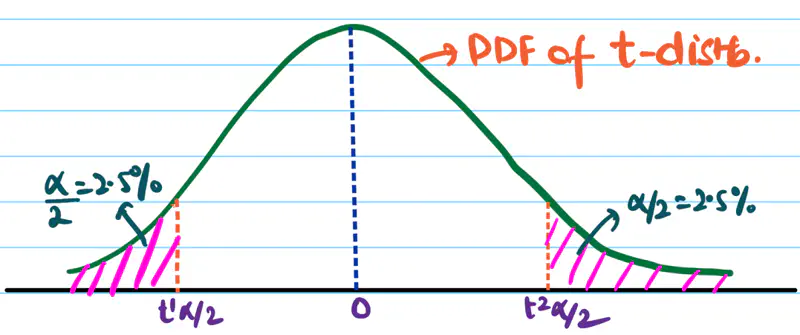
images/maths/statistics/two_sided.png

So, we want \(t_{obs}\) to be very negative or very positive to confidently conclude that the alternate hypothesis is true. We accept \(H_a\) if \(t_{obs} < t^1_{\alpha/2}\) or \(t_{obs} > t^2_{\alpha/2}\).

Note: For critical applications ‘\(\alpha\)’ can be very small i.e. 0.1% or 0.01%, e.g medicine.

Left Tailed | Right Tailed | Two Tailed or Sided HypothesisTest | Explained with Example
Significance Level (\(\alpha\))

It is the probability of wrongly rejecting a true null hypothesis, known as a Type I error or false +ve rate.

  • Tolerance level of wrongly accepting alternate hypothesis.
  • If the p-value < \(\alpha\), we reject the null hypothesis and conclude that the finding is statistically NOT so significant..
Critical Value

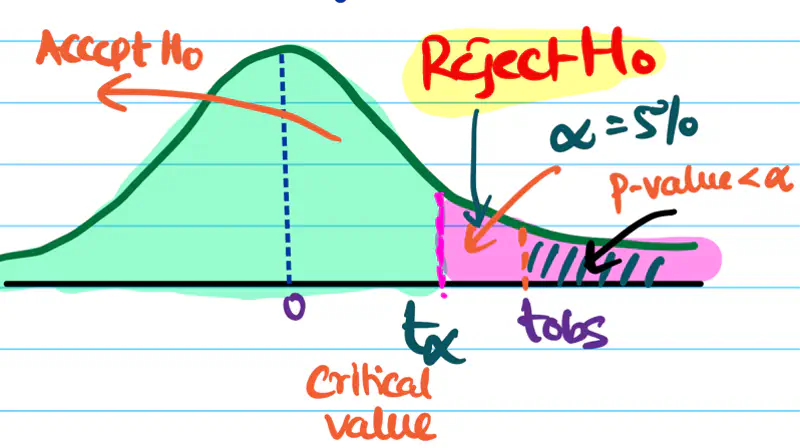
It is a specific point on the test-statistic distribution that defines the boundaries of the null hypothesis acceptance/rejection region.

  • It tells us that at what value (\(t_{\alpha}\)) of test statistic will the area under curve be equal to the significance level \(\alpha\).

  • For a right tailed/sided test:

    • if \(t_{obs} > t_{\alpha} => p_{value} < \alpha\); therefore, reject null hypothesis.
    • if \(t_{obs} < t_{\alpha} => p_{value} \ge \alpha\); therefore, failed to reject null hypothesis.
    images/maths/statistics/critical_value.png

Power of Test

It is the probability that a hypothesis test will correctly reject a false null hypothesis (\(H_{0}\)) when the alternative hypothesis (\(H_{a}\)) is true.

  • Power of test = \(1 - \beta\)

  • Probability of correctly accepting alternate hypothesis (\(H_{a}\))

  • \(\alpha\): Probability of wrongly accepting alternate hypothesis \(H_{a}\)

  • \(\beta\): Probability of wrongly rejecting alternate hypothesis \(H_{a}\)

    images/maths/statistics/power_of_test.png

Does having a large sample size make a hypothesis test more powerful?

Yes, having a large sample size makes a hypothesis test more powerful.

  • As n increases, sample mean \(\bar{x}\) approaches the population mean \(\mu\).
  • Also, as n increases, t-distribution approaches normal distribution.
Power of a Test in Hypothesis Testing | Explained with Example
P-Value
P-value only measures whether the observed change is statistically significant.
Effect Size

It is a standardized objective measure that complements p-value by clarifying whether a statistically significant finding has any real world relevance.
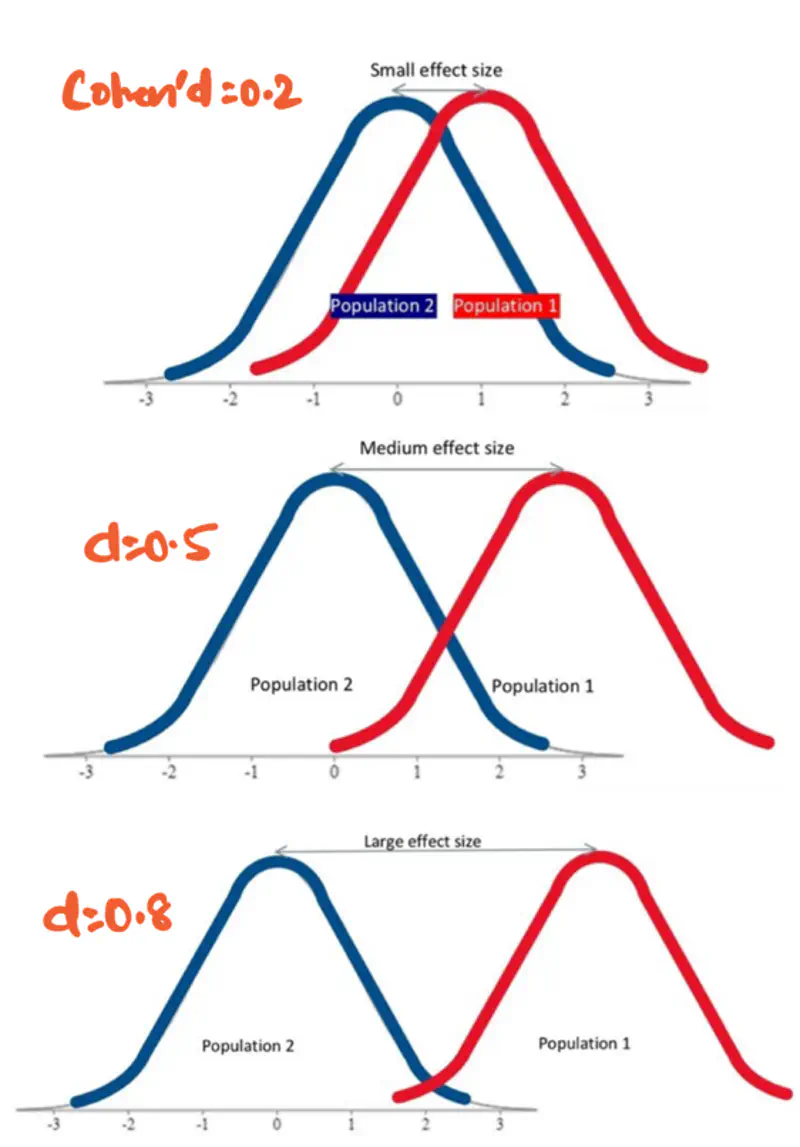
It quantifies the magnitude of relationship between two variables.

  • Larger effect size => more impactful effect.
  • Standardized (mean centered + variance scaled) measure allows us to compare the imporance of effect across various studies or groups, even with different sample sizes.

Effect size is measured using Cohen’s d formula:

\[ d = \frac{\bar{X_1} - \bar{X_2}}{s_p} \\[10pt] s_p = \sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}} \]

\(\bar{X}\): Sample mean
\(s_p\): Pooled Standard deviation
\(n\): Sample size
\(s\): Standard deviation

Note: Theoretically, Cohen’s d value can range from negative infinity to positive infinity.
but for practical purposes, we use the following value:
small effect (\(d=0.2\)), medium effect (\(d=0.5\)), and large effect (\(d\ge 0.8\)).

  • More overlap => less effect i.e low Cohen’s d value.

    images/maths/statistics/effect_size.png
Example
  • A study on drug trials finds that patients taking a new drug had statistically significant
    improvement (p-value<0.05), compared to a placebo group.
  1. Small effect size: Cohen’s d = 0.1 => drug had minimal effect.
  2. Large effect size: Cohen’s d = 0.8 => drug produced substantial improvement.
Understanding Effect Size | Cohen’s d - How big is the effect | Hypothesis Testing | Explained

End of Section