T-Test

Student’s T-Test

  5 minute read  

In this section, we will understand Student’s T-Test.


📘

T-Test:
It is a statistical test that is used to determine whether the sample mean is equal to a hypothesized value or
is there a significant difference between the sample means of 2 groups.

  • It is a parametric test, since it assumes data to be approximately normally distributed.
  • Appropriate when:
    • sample size n < 30.
    • population standard deviation \(\sigma\) is unknown.
  • It is based on Student’s t-distribution.

📘

Student’s t-distribution:
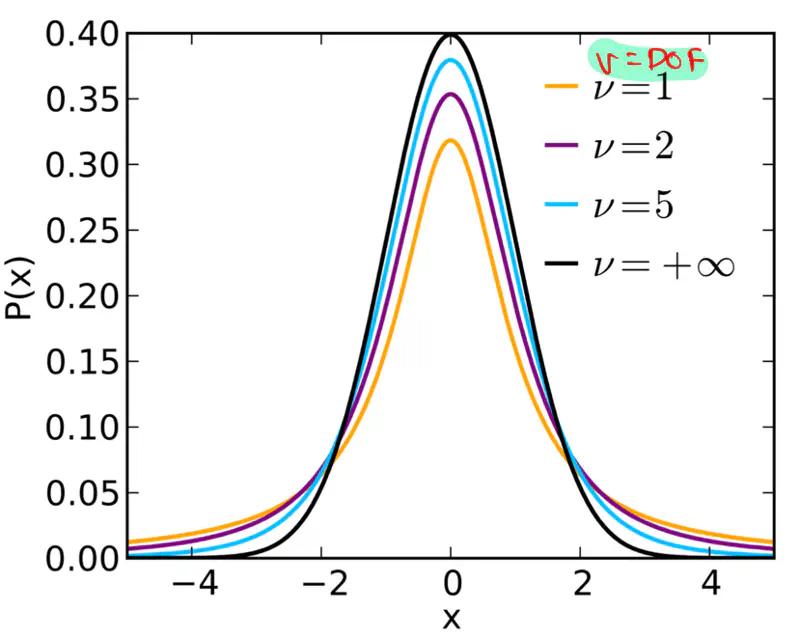
It is a continuous probability distribution that is a symmetrical, bell-shaped curve similar to the normal distribution but with heavier tails.

  • Shape of the curve or mass in tail is controlled by degrees of freedom.

There are 3 types of T-Test:

  1. 1-Sample T-Test: Test if sample mean differs from hypothesized value.
  2. 2-Sample T-Test: Test whether there is a significant difference between the means of two independent groups.
  3. Paired T-Test: Test whether 2 related samples differ, e.g., before and after.


📘

1-Sample T-Test:
It is used to test whether the sample mean is equal to a known/hypothesized value.
Test statistic (t):

\[ t = \frac{\bar{x} - \mu}{s/\sqrt{n}} \]

where,
\(\bar{x}\): sample mean
\(\mu\): hypothesized value
\(s\): sample standard deviation
\(n\): sample size
\(\nu = n-1 \): degrees of freedom

💡 A developer claims that the new algorithm improves API response time by 100 ms, on an average.
Tester ran the test 20 times and found the average API repsonse time to be 115 ms, with a standard deviation of 25 ms.
Is the developer’s claim valid?

Let’s verify developer’s claim using the tester’s test results using 1 sample t-test.
Null hypothesis: \(H_0\) = The average API response time is 100 ms, i.e, \(\bar{x} = \mu\).
Alternative hypothesis: \(H_a\) = The average API response time > 100 ms, i.e, \(\bar{x} > \mu\) => right tailed test.
Hypothesized mean \(\mu\) = 100 ms
Sample mean \(\bar{x}\) = 115 ms
Sample standard deviation \(s\) = 25 ms
Sample size \(n\) = 20
Degrees of freedom \(\nu\) = 19

\( t_{obs} = \frac{\bar{x} - \mu}{s/\sqrt{n}}\) = \(\frac{115 - 100}{25/\sqrt{20}}\)
= \(\frac{15\sqrt{20}}{25} = \frac{3\sqrt{20}}{5} \approx 2.68\)

Let significance level \(\alpha\) = 5% =0.05.
Critical value \(t_{0.05}\) = 1.729
Important: Find the value of \(t_{\alpha}\) in T-table

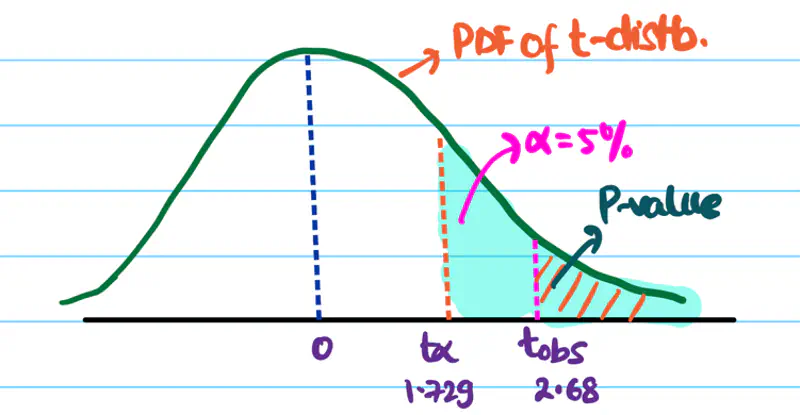
Since \(t_{obs}\) > \(t_{0.05}\), we reject the null hypothesis.
And, accept the alternative hypothesis that the API response time is significantly > 100 ms.
Hence, the developer’s claim is NOT valid.



📘

2-Sample T-Test:
It is used to determine whether there is a significant difference between the means of two independent groups.
There are 2 types of 2-sample t-test:

  1. Unequal Variance
  2. Equal Variance

Unequal Variance:
In this case, the variance of 2 independent groups is not equal.
Also called, Welch’s t-test.
Test statistic (t):

\[ t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \\[10pt] \text{ Degrees of freedom (Welch-Satterthwaite): } \\[10pt] \nu = \frac{[\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}]^2}{\frac{s_1^4}{n_1^2(n_1-1)} + \frac{s_2^4}{n_2^2(n_2-1)}} \]

Equal Variance:
In this case, both samples come from equal or approximately equal variance.
Test statistic (t):

\[ t = \frac{\bar{x}_1 - \bar{x}_2}{s_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \\[10pt] \text{ Pooled variance } s_p: \\[10pt] s_p = \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}} \]

Here, degrees of freedom (for equal variance) \(\nu\) = \(n_1 + n_2 - 2\).

\(\bar{x}\): sample mean
\(s\): sample standard deviation
\(n\): sample size
\(\nu\): degrees of freedom

💡

The AI team wants to validate whether the new ML model accuracy is better than the existing model’s accuracy.
Below is the data for the existing model and the new model.

New Model (A)Existing Model (B)
Sample size (n)2418
Sample mean (\(\bar{x}\))91%88%
Sample std. dev. (s)4%3%

Given that the variance of accuracy scores of new and existing models are almost same.

Now, let’s follow our hypothesis testing framework.
Null hypothesis: \(H_0\): The accuracy of new model is same as the accuracy of existing model.
Alternative hypothesis: \(H_a\): The new model’s accuracy is better/greater than the existing model’s accuracy => right tailed test

Let’s solve this using 2 sample T-Test, since the sample size n < 30.
Since the variance of 2 sample are almost equal then we can use the pooled variance method.

Next let’s compute the test statistic, under null hypothesis.

\[ s_p = \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}} \\[10pt] = \sqrt{\frac{(23)4^2 + (17)3^2}{24+18-2}} \\[10pt] = \sqrt{\frac{23*16 + 17*9}{40}} = \sqrt{\frac{521}{40}} \\[10pt] => s_p \approx 3.6 \\[10pt] t_{obs} = \frac{\bar{x}_1 - \bar{x}_2}{s_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \\[10pt] = \frac{91-88}{3.6\sqrt{\frac{1}{24} + \frac{1}{18}}} \\[10pt] = \frac{3}{3.6*0.31} \\[10pt] => t_{obs} \approx 2.68 \\[10pt] \]

DOF \(\nu\) = \(24+18-2\) = 42 - 2 = 40
Let significance level \(\alpha\) = 5% =0.05.
Critical value \(t_{0.05}\) = 1.684
Important: Find the value of \(t_{\alpha}\) in T-table

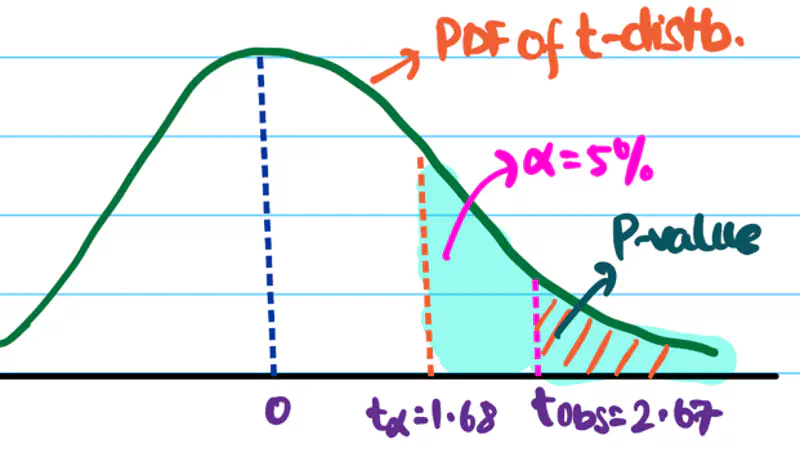
Since \(t_{obs}\) > \(t_{0.05}\), we reject the null hypothesis.
And, accept the alternative hypothesis that the new model has better accuracy than the existing model.




End of Section